Trong hai mệnh đề toán học sau đây, mênh đề nào là một khẳng định đúng? Mệnh đề nào là một khẳng định sai?

P: “Tổng hai góc đối của một tứ giác nội tiếp bằng \({180^o}\)”

Q: “\(\sqrt 2 \) là số hữu tỉ”

Bài 1 :

Câu nào dưới đây không là một mệnh đề?

Bài 2 :

Trong các mệnh đề sau, mệnh đề nào sai?

Bài 3 :

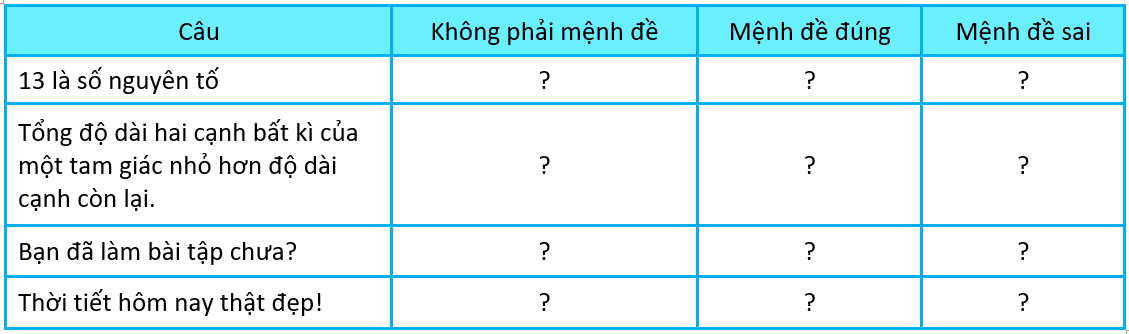
Thay dấu “?” bằng dấu “x” vào ô thích hợp trong bảng sau:

Bài 4 :

Trong các câu ở tình huống mở đầu:

a) Câu nào đúng?

b) Câu nào sai?

c) Câu nào không xác định được tính đúng sai?

Bài 5 :

Trong các câu sau, câu nào là mệnh đề?

a) Trung Quốc là nước đông dân nhất thế giới;

b) Bạn học trường nào?

c) Không được làm việc riêng trong giờ học;

d) Tôi sẽ sút bóng trúng xà ngang.

Bài 6 :

Xác định tính đúng sai của mỗi mệnh đề sau:

a) \(\pi  > \dfrac{{10}}{3};\)

b) Phương trình \(3x + 7 = 0\) có nghiệm;

c) Có ít nhất một số cộng với chính nó bằng 0;

d) 2022 là hợp số.

Bài 7 :

Câu nào sau đây không là mệnh đề?

A. Tam giác đều là tam giác có ba cạnh bằng nhau.

B. \(3\;\, < 1\)

C. \(4 - 5 = 1\)

D. Bạn học giỏi quá!

Bài 8 :

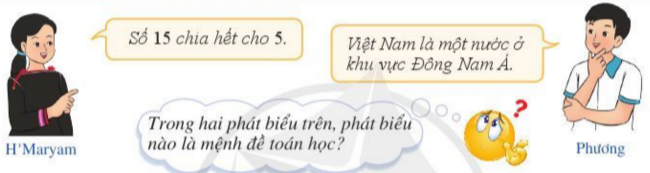
Trong hai phát biểu trên, phát biểu nào là mệnh đề toán học?

Bài 9 :

Nêu ví dụ về một mệnh đề đúng và một mệnh đề sai.

Bài 10 :

Nêu hai ví dụ về mệnh đề toán học.

Bài 11 :

a) Phát biểu của bạn H’Maryam có phải là một câu khẳng định về tính chất chia hết trong toán học hay không?

b) Phát biểu của bạn phương có phải là một câu khẳng định về một sự kiện trong toán học hay không?

Bài 12 :

Trong các phát biểu sau, phát biểu nào là mệnh đề toán học?

a) Tích hai số thực trái dấu là một số thực âm.

b) Mọi số tự nhiên đều là dương.

c) Có sự sống ngoài Trái Đất

d) Ngày 1 tháng 5 là ngày Quốc tế Lao động.

Bài 13 :

Phát biểu nào sau đây không là một mệnh đề toán học?

a) Tích của ba số tự nhiên liên tiếp luôn chia hết cho 3.

b) Nếu \(\widehat {AMB} = {90^o}\) thì M nằm trên đường tròn đường kính AB.

c) Ngày 2 tháng 9 là ngày Quốc Khánh của nuốc Cộng hòa Xã hội chủ nghĩa Việt Nam

d) Mọi số nguyên tố đều là số lẻ

Bài 14 :

Xét tính đúng sai của các mệnh đề sau:

a) Vịnh Hạ Long là di sản thiên nhiên thế giới.

b) \(\sqrt {{{( - 5)}^2}}  =  - 5\)

c) \({5^2} + {12^2} = {13^2}\)

Bài 15 :

Trong các câu sau, câu nào là mệnh đề?

a) \(\sqrt 2 \) là số vô tỉ

b) \(\frac{1}{{\sqrt 2 }} + \frac{1}{{\sqrt 3 }} + ... + \frac{1}{{\sqrt {10} }} > 2\)

c) 100 tỉ là số rất lớn

d) Trời hôm nay đẹp quá!

Bài 16 :

Xét các câu sau đây:

(1) 1+1=2.

(2) Dân ca Quan họ là di sản văn hóa phi vật thể đại diện của nhân loại.

(3) Dơi là một loài chim

(4) Nấm có phải là một loài thực vật không?

(5) Hoa hồng đẹp nhất trong các loài hoa.

(6) Trời ơi, nóng quá!

Trong những câu trên,

a) Câu nào là khẳng định đúng, câu nào là khẳng định sai?

b) Câu nào không phải là khẳng định?

c) Câu nào là khẳng định, nhưng không thể xác định nó đúng hay sai?

Bài 17 :

Xác định tính đúng sai của mỗi mệnh đề sau:

a) \(\{ a\}  \in \{ a;b;c;d\} \)

b) \(\emptyset  = \{ 0\} \)

c) \(\{ a;b;c;d\}  \in \{ b;a;d;c\} \)

d) \(\{ a;b;c\}  \not \subset \{ a;b;c\} \)

Bài 18 :

Xác định tính đúng sai của mỗi mệnh đề sau:

a) Nếu \(2a - 1 > 0\) thì \(a > 0\) (a là số thực cho trước).

b) \(a - 2 > b\) nếu và chỉ nếu \(a > b + 2\) (a, b là hai số thực cho trước).

Bài 19 :

Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?

Bài 20 :

Cho mệnh đề P: “x + 1 < x”, Q: “x + 1 > x”. Xét tính đúng sai của hai mệnh đề P, Q.

A. P đúng, Q sai

B. P sai, Q đúng

C. P, Q đều đúng

D. P, Q đều sai

Bài 21 :

Xác định tính đúng sai của các mệnh đề sau:

a) Các số nguyên tố đều là số lẻ;

b) Phương trình \({x^2} + 1 = 0\) có hai nghiệm nguyên phân biệt;

c) Mọi số nguyên lẻ đều không chia hết cho 2.

Bài 22 :

Điền Đ vào ô trống nếu mệnh đề đúng, điền S vào ô trống nếu mệnh đề sai.

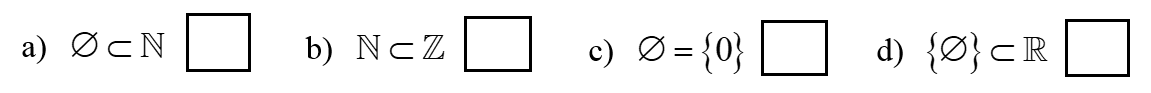
Bài 23 :

Xét tính đúng sai của các mệnh đề sau:

a) Mọi số tự nhiên có tận cùng bằng 0 đều chia hết cho 10

b) Bình phương của mọi số thực đều lớn hơn 0

c) Tập rỗng là tập con của mọi tập hợp

Bài 24 :

Cho x, y là hai số thực cùng khác -1. Kết luận nào sau đây là đúng?

A. \(x + y + xy \ne  - 1\)

B. \(x + y + xy =  - 1\)

C. \(x + y \ne  - 2\)

D. \(xy \ne  - 1\)

Bài 25 :

Trong các câu sau, câu nào là mệnh đề?

A. \(6 + x = 4{x^2}.\)

B. \(a < 2.\)

C. \(123\) là số nguyên tố phải không?

D. Bắc Giang là tỉnh thuộc miền Nam Việt Nam.

Bài 26 :

Trong các mệnh đề sau, mệnh đề nào đúng?

A. \(\emptyset  = \left\{ 0 \right\}.\)

B. \(\emptyset  \subset \left\{ 0 \right\}.\)

C. \(\left\{ 0 \right\} \subset \emptyset .\)

D. \(0 \subset \emptyset .\)

Bài 27 :

Mệnh đề nào sau đây đúng?

A. Nếu a là số tự nhiên thì a là số hữu tỉ không âm.

B. Nếu a là số hữu tỉ không âm thì a là số tự nhiên.

C. Nếu a là số hữu tỉ dương thì a là số tự nhiên.

D. Nếu a không là số tự nhiên thì a không phải là số hữu tỉ không âm.

Bài 28 :

Cho x là một phần tử của tập hợp \(X.\) Xét các mệnh đề sau:

\(\left( I \right)\,\,x \in X;\)

\(\left( {II} \right)\,\,\left\{ x \right\} \in X;\)

\(\left( {III} \right)\,\,x \subset X;\)

\(\left( {IV} \right)\,\,\left\{ x \right\} \subset X.\)

Trong các mệnh đề trên, mệnh đề nào đúng?

A. \(\left( I \right)\) và \(\left( {II} \right)\)

B. \(\left( I \right)\) và \(\left( {III} \right)\)

C. \(\left( I \right)\) và \(\left( {IV} \right)\)

D. \(\left( {II} \right)\) và \(\left( {IV} \right)\)

Bài 29 :

Cho hai tập hợp \(X = \left\{ {n \in N|n} \right.\) là bội của \(2\) và \(\left. 3 \right\},\) \(Y = \left\{ {n \in N|n} \right.\) là bội của \(\left. 6 \right\}.\) Trong các mệnh đề sau, mệnh đề nào sai?

A. \(Y \subset X.\)

B. \(X \subset Y.\)

C. \(\exists n:n \in X\) và \(n \notin Y.\)

D. \(X = Y.\)

Bài 30 :

Mệnh đề "\(\exists x \in ,{x^2} = 15\)" được phát biểu là:

A. Bình phương của mỗi số thực bằng 15.

B. Có ít nhất một số thực mà bình phương của nó bằng 15.

C. Chỉ có một số thực mà bình phương của nó bằng 15.

D. Nếu \(x\) là một số thực thì \({x^2} = 15.\)