Tính đối xứng là một yếu tố tạo nên sự cân đối, hài hoà của các hình. Tuy nhiên, không phải lúc nào ta cũng có thể gấp hình để biết hình có trục đối xứng hay không. Em hãy quan sát và vẽ phác trục đối xứng của hình Tháp Chàm và ngôi sao sáu cánh dưới đây (nếu có).

 

Bài 1 :

Trong các hình dưới đây, hình nào có trục đối xứng?

Bài 2 :

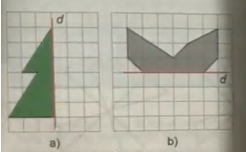
Vẽ các hình sau vào giấy kẻ ô vuông rồi vẽ thêm để được hình nhận đường thẳng d là trục đối xứng.

Bài 3 :

 Quan sát hình con bướm ở hình bên. Em thấy điều gì khi hai cánh của con bướm gập lại?

Bài 4 :

Bài 5 :

Trong các hình 48,49,50, hình nào có trục đối xứng? nếu là hình có trục đối xứng, hãy chỉ ra trục đối xứng của hình đó 

Bài 6 :

Hãy tìm một số hình đối xứng trong thực tiễn

Bài 7 :

Hãy quan sát xung quanh và chỉ ra những hình:

Có trục đối xứng;

Bài 8 :

Trong các biểu tượng sau, biểu tượng nào có trục đối xứng?

Bài 9 :

Trong các công trình được minh họa ở Hình 37, các hình từ a) đến c), công trình nào có trục đối xứng?

Bài 10 :

Trong các hình sau, hình nào có trục đối xứng?

Bài 11 :

Bài 12 :

Bài 13 :

Hình nào sau đây có trục đối xứng? Hãy chỉ ra trục đối xứng (nếu có).

Bài 14 :

Hình nào sau đây có trục đối xứng?

Bài 15 :

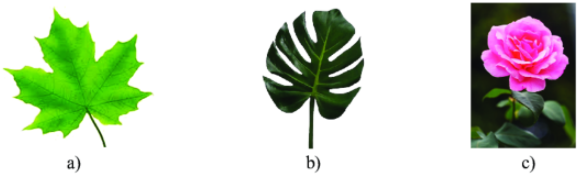
Hình hai chiếc lá và hình bông hoa sau đây, hình nào có trục đối xứng?

Bài 16 :

Hãy so sánh sự giống nhau về hình dạng và tính năng của con chuồn chuồn và chiếc máy bay trong hai hình dưới đây:

Bài 17 :

Tìm một số hình có trục đối xứng trong thực tiễn.

Bài 18 :

Trong các biển báo giao thông sau, biển báo nào có trục đối xứng?

Bài 19 :

Tìm các dụng cụ lao động có trục đối xứng