Nội dung từ Loigiaihay.Com
Lớp 10C có 45 học sinh, trong đó có 18 học sinh tham gia cuộc thi vẽ đồ họa trên máy tính, 24 học sinh tham gia cuộc thi tin học văn phòng cấp trường và 9 học sinh không tham gia cả hai cuộc thi này. Hỏi có bao nhiêu học sinh của lớp 10C tham gia đồng thời hai cuộc thi?
Gọi A là tập hợp các học sinh tham gia cuộc thi vẽ đồ họa trên máy tính và B là tập hợp các học sinh tham gia cuộc thi tin học văn phòng cấp trường.
Vẽ biểu đồ Ven.
Gọi X là tập hợp các học sinh của lớp 10C.
A là tập hợp các học sinh tham gia cuộc thi vẽ đồ họa trên máy tính,
B là tập hợp các học sinh tham gia cuộc thi tin học văn phòng cấp trường.
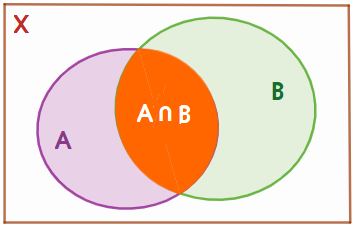
Theo biểu đồ Ven ta có: \(n(A) = 18,\;n(B) = 24,\;n(X) = 45.\)
\(n(A \cup B)\) là số học sinh tham gia ít nhất một trong hai cuộc thi, bằng: 45 -9 = 36 (học sinh)
Mà \(n(A \cup B) = n(A) + n(B) - n(A \cap B)\) (do các học sinh tham gia cả 2 cuộc thi được tính hai lần)
Suy ra số học sinh tham gia cả 2 cuộc thi là: \(n(A \cap B) = 18 + 24 - 36 = 6\)
Vậy có 6 học sinh của lớp 10C tham gia đồng thời hai cuộc thi.

Các bài tập cùng chuyên đề
Cho A là tập hợp các bội của 2, B là tập hợp các bội của 8. Chọn khẳng định đúng:
Câu lạc bộ Lịch sử có 12 thành viên (không có hai bạn nào trùng tên), tổ chức hai chuyên đề trên một phần mềm họp trực tuyến. Tên các thành viên tham gia mỗi chuyên đề được hiển thị trên màn hình.
Hỏi: Có bao nhiêu thành viên vắng mặt trong cả hai chuyên đề?

Cho \(A = \left\{ {x \in \mathbb{Z}|\;x < 4} \right\},\)
\( \,B = \left\{ {x \in \mathbb{Z}|\;\left( {5x - 3{x^2}} \right)\left( {{x^2} + 2x - 3} \right) = 0} \right\}\)
a) Liệt kê các phần tử của hai tập hợp A và B.
b) Hãy xác định các tập hợp \(A \cap B,A \cup B\) và \(A\,{\rm{\backslash }}\,B\)
Xác định các tập hợp sau và biểu diễn chúng trên trục số.
a) \(( - 4;1] \cap [0;3)\)
b) \((0;2] \cup (- 3;1]\)
c) \(( - 2;1] \cap (1;+ \infty )\)
d) \(\mathbb{R}{\rm{\backslash }}( - \infty ;3]\)
Để phục vụ cho một hội nghị quốc tế, ban tổ chức huy động 35 người phiên dịch tiếng Anh, 30 người phiên dịch tiếng Pháp, trong đó có 16 người phiên dịch được cả hai thứ tiếng Anh và Pháp. Hãy trả lời các câu hỏi sau:
a) Ban tổ chức đã huy động bao nhiêu người phiên dịch cho hội nghị đó?
b) Có bao nhiêu người chỉ phiên dịch được tiếng Anh?
c) Có bao nhiêu người chỉ phiên dịch được tiếng Pháp?
Cho \(A = \left\{ {x \in \mathbb{N}|\;x < 7} \right\},\) \(\,B = \left\{ {1;2;3;6;7;8} \right\}\). Xác định các tập hợp sau:
\(A \cup B,\;A \cap B,\;A\,{\rm{\backslash }}\,B\)
Cho \(A = [-2;3],\;\,B = (1; + \infty )\). Xác định các tập hợp sau:
\(\;A \cap B; B \backslash A \) và \({C_\mathbb{R}}B\)
Xác định các tập hợp sau và biểu diễn chúng trên trục số.
a) \(( - \infty ;1) \cap (0; + \infty )\)
b) \((4;7] \cup ( - 1;5)\)
c) \((4;7]\;{\rm{\backslash }}\;( - 3;5]\)
Một cuộc khảo sát về khách du lịch thăm vịnh Hạ Long cho thấy 1 410 khách du lịch được phỏng vấn có 789 khách du lịch đến thăm động Thiên Cung, 690 khách du lịch đến đảo Titop. Toàn bộ khách được phỏng vấn đã đến ít nhất một trong hai địa điểm trên. Hỏi có bao nhiêu khách du lịch vừa đến thăm động Thiên cung vừa đến thăm đảo Titop ở vịnh Hạ Long?
Câu lạc bộ Lịch sử có 12 thành viên (không có hai bạn nào trùng tên) tổ chức hai chuyên đề trên một phần mềm họp trực tuyến. Tên các thành viên tham gia mỗi chuyên được hiển thị trên màn hình (H.1.1).
Xác định các tập hợp sau và biểu diễn chúng trên trục số:
a) \([ - 3;7] \cap (2;5)\)
b) \(( - \infty ;0] \cup ( - 1;2)\)
c) \(\mathbb{R}\,{\rm{\backslash }}\,( - \infty ;3)\)
d) \(( - 3;2)\,{\rm{\backslash }}\,[1;3)\)
Gọi A là tập nghiệm của phương trình \({x^2} + x - 2 = 0\),
B là tập nghiệm của phương trình \(2{x^2} + x - 6 = 0\)
Tìm \(C = A \cap B\).
Tìm \(D = E \cap G\) biết E và G lần lượt là tập nghiệm của hai bất phương trình trong mỗi trường hợp sau:
a) \(2x + 3 \ge 0\) và \( - x + 5 \ge 0\)
b) \(x + 2 > 0\) và \(2x - 9 < 0\)
Lớp 10B có 28 học sinh tham gia câu lạc bộ thể thao và 19 học sinh tham gia câu lạc bộ âm nhạc. Biết rằng có 10 học sinh tham gia cả hai câu lạc bộ trên.
a) Có bao nhiêu học sinh ở lớp 10B tham gia câu lạc bộ thể thao và không tham gia câu lạc bộ âm nhạc?
b) Có bao nhiêu học sinh ở lớp 10B tham gia ít nhất một trong hai câu lạc bộ trên?
c) Biết lớp 10B có 40 học sinh. Có bao nhiêu học sinh không tham gia câu lạc bộ thể thao? Có bao nhiêu học sinh không tham gia cả hai câu lạc bộ?
Một nhóm có 12 học sinh chuẩn bị cho hội diễn văn nghệ. Trong danh sách đăng kí tham gia tiết mục múa và tiết mục hát của nhóm đó, có 5 học sinh tham gia tiết mục múa, 3 học sinh tham gia cả hai tiết mục. Hỏi có bao nhiêu học sinh trong nhóm tham gia tiết mục hát? Biết có 4 học sinh của nhóm không tham gia tiết mục nào.
Giải Bóng đá vô địch thế giới World Cup 2018 được tổ chức ở Liên bang Nga gồm 32 đội. Sau vòng thi đấu bảng, Ban tổ chức chọn ra 16 đội chia làm 8 cặp đấu loại trực tiếp. Sau vòng đấu loại trực tiếp đó, Ban tổ chức tiếp tục chọn ra 8 đội chia làm 4 cặp đấu loại trực tiếp ở vòng tứ kết. Gọi A là tập hợp 32 đội tham gia World Cup 2018, B là tập hợp 16 đội sau vòng thi đấu bảng, C là tập hợp 8 đội thi đấu vòng tứ kết.
a) Sắp xếp các tập hợp A, B, C theo quan hệ “\( \subset \)”.
b) So sánh hai tập hợp \(A \cap C\) và \(B \cap C\).
c) Tập hợp \(A\,{\rm{\backslash }}\,B\) gồm những đội bóng bị loại sau vòng đấu nào?
Cho hai tập hợp: \(A = [0;3]\), \(B = (2; + \infty )\). Xác định \(A \cap B,A \cup B,\)\(A\,{\rm{\backslash }}\,B,B\,{\rm{\backslash }}\,A,\mathbb{R}\,{\rm{\backslash }}\,B.\)
Gọi E là tập nghiệm của phương trình \({x^2} - 2x - 3 = 0\).
G là tập nghiệm của phương trình \((x + 1)(2x - 3) = 0\)
Tìm \(P = E \cap G\).
Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập con của tập hợp còn lại? Chúng có bằng nhau không?
a) \(A = \{ - \sqrt 3 ;\sqrt 3 \} \) và \(B = \{ x \in \mathbb{R}|{x^2} - 3 = 0\} \)
b) C là tập hợp các tam giác đều và D là tập hợp các tam giác cân;
c) \(E = \{ x \in \mathbb{N}|x\) là ước của 12\(\} \) và \(F = \{ x \in \mathbb{N}|x\) là ước của 24\(\} .\)
Viết tất cả các tập con của tập hợp \(A = \{ a;b\} .\)
Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập con của tập còn lại? Chúng có bằng nhau không?
a) \(A = \{ x \in \mathbb{N}|\;x < 2\} \) và \(B = \{ x \in \mathbb{R}|\;{x^2} - x = 0\} \)
b) C là tập hợp các hình thoi và D là tập hợp các hình vuông
c) \(E = ( - 1;1]\) và \(F = ( - \infty ;2]\)
Tại vòng chung kết của một trò chơi trên truyền hình, có 100 khán giả tại trường quay có quyền bình chọn cho hai thí sinh A và B. Biết rằng có 85 khán giả bình chọn cho thí sinh A, 72 khán giả bình chọn cho thí sinh B và 60 khán giả bình chọn cho cả hai thí sinh. Có bao nhiêu khán giả đã tham gia bình chọn? Có bao nhiêu khán giả không tham gia bình chọn?
Xác định các tập hợp \(A \cup B\) và \(A \cap B\), biết:
a) \(A = \{ a;b;c;d;e\} \), \(B = \{ a;e;i;u\} \)
b) \(A = \{ x \in \mathbb{R}|\;{x^2} + 2x - 3 = 0\} \),\(B = \{ x \in \mathbb{R}|\;|x|\; = 1\} \)
Bảng sau đây cho biết kết quả vòng phỏng vấn tuyển dụng vào một công ty (dấu “+” là đạt, dấu “-” là không đạt):

a) Xác định tập hợp A gồm các ứng viên đạt yêu cầu về chuyên môn, tập hợp B gồm các ứng viên đạt yêu cầu về ngoại ngữ.
b) Xác định tập hợp C gồm các ứng viên đạt yêu cầu cả về chuyên môn và ngoại ngữ.
c) Xác định tập hợp D gồm các ứng viên đạt ít nhất một trong hai yêu cầu về chuyên môn và ngoại ngữ.

Xác định các tập hợp \(A \cup B\) và \(A \cap B\) với
a) A = {đỏ; cam; vàng; lục; lam}, B = {lục; lam; chàm; tím}.
b) A là tập hợp các tam giác đều, B là tập hợp các tam giác cân.
Cho \(E = \{ x \in \mathbb{N}|x < 10\} ,A = \{ x \in E|x\)là bội của 3\(\} ,\)\(B = \{ x \in E|x\) là ước của 6\(\} .\)
Xác định các tập hợp \(A\backslash B,{\rm{ }}B\backslash A,\;{C_E}A,\;{C_E}B,{C_E}(A \cup B),{C_E}(A \cap B).\)
Cho A và B là hai tập hợp bất kì. Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập con của tập hợp còn lại? Hãy giải thích bằng cách sử dụng biểu đồ Ven.
a) A và \(A \cup B\)
b) A và \(A \cap B\)
Trong số 35 học sinh của lớp 10H, có 20 học sinh thích môn Toán, 16 học sinh thích môn Tiếng Anh và 12 học sinh thích cả hai môn này. Hỏi lớp 10H:
a) Có bao nhiêu học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh?
b) Có bao nhiêu học sinh không thích cả hai môn này?
Xác định các tập hợp sau đây:
a) \(( - \infty ;0] \cup [ - \pi ;\pi ]\)
b) \([ - 3,5;2] \cap ( - 2;3,5)\)
c) \(( - \infty ;\sqrt 2 ] \cap [1; + \infty )\)
d) \(( - \infty ;\sqrt 2 ]{\rm{\backslash }}[1; + \infty )\)
Cho \(A = \{ x \in \mathbb{R}|{x^2} - 5x - 6 = 0\} ,\)\(B = \{ x \in \mathbb{R}|{x^2} = 1\} .\)
Tìm \(A \cap B,A \cup B,A\backslash B,{\rm{ }}B\backslash A.\)
Cho \(A = \{ x \in \mathbb{R}|1 - 2x \le 0\} ,\)\(B = \{ x \in \mathbb{R}|x - 2 < 0\} .\)
Tìm \(A \cap B,A \cup B.\)












