Nội dung từ Loigiaihay.Com
Đề bài
Hàm số $y = {x^3} - 3{{\rm{x}}^2} + 4$ đồng biến trên:
-
A.
$\left( {0;2} \right)$
-
B.
$\left( { - \infty ;0} \right)$ và $\left( {2; + \infty } \right)$
-
C.
$\left( { - \infty ;2} \right)$
-
D.
$\left( {0; + \infty } \right)$
Phương pháp giải
- Bước 1: Tìm TXĐ của hàm số.
- Bước 2: Tính đạo hàm $f'\left( x \right)$, tìm các điểm ${x_1},{x_2},...,{x_n}$ mà tại đó đạo hàm bằng $0$ hoặc không xác định.
- Bước 3: Xét dấu đạo hàm và nêu kết luận về khoảng đồng biến, nghịch biến của hàm số.
+ Các khoảng mà $f'\left( x \right) > 0$ là các khoảng đồng biến của hàm số.
+ Các khoảng mà $f'\left( x \right) < 0$ là các khoảng nghịch biến của hàm số.
Lời giải của GV HocTot.XYZ
TXĐ: $D=R$
Ta có: $y' = 3{{\rm{x}}^2} - 6{\rm{x}}$
$ \Rightarrow y' = 0 \Leftrightarrow x = 0$ hoặc $x = 2$
Ta có bảng biến thiên
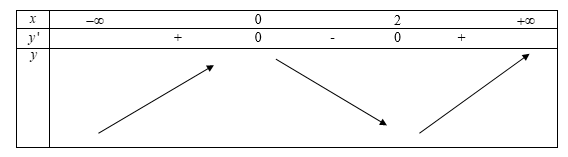
Vậy hàm số đồng biến trên các khoảng $\left( { - \infty ;0} \right)$ và $\left( {2; + \infty } \right)$.
Đáp án : B
Chú ý
Cần tránh trường hợp xét dấu đạo hàm sai dẫn đến chọn nhầm đáp án A.
Các bài tập cùng chuyên đề