Nội dung từ Loigiaihay.Com
Cho tam giác ABC, chứng minh rằng:
a) tanA+tanB+tanC=tanA.tanB.tanC
(với điều kiện tam giác ABC không vuông)
b) tanA2.tanB2+tanB2.tanC2+tanC2.tanA2=1
Sử dụng định lí tổng ba góc trong một tam giác: A+B+C=π.
Sử dụng công thức tan(a+b)=tana+tanb1−tanatanb.
Trong tam giác ABC, ta có A+B+C=π.
a) Do A+B+C=π⇒A+B=π−C⇒tan(A+B)=tan(π−C)
Vì tan(A+B)=tanA+tanB1−tanAtanB, tan(π−C)=tan(−C)=−tanC, nên:
tan(A+B)=tan(π−C)⇒tanA+tanB1−tanAtanB=−tanC
⇒tanA+tanB=−(1−tanAtanB)tanC
⇒tanA+tanB=−tanC+tanAtanBtanC⇒tanA+tanB+tanC=tanAtanBtanC
Bài toán được chứng minh.
b) Ta có:
A+B+C=π⇒A+B+C2=π2⇒A+B2=π2−C2⇒tan(A2+B2)=tan(π2−C2)Do tan(A2+B2)=tanA2+tanB21−tanA2tanB2 và tan(π2−C2)=cotC2=1tanC2, nên:
tan(A2+B2)=tan(π2−C2)⇒tanA2+tanB21−tanA2tanB2=1tanC2
⇒(tanA2+tanB2)tanC2=1−tanA2tanB2⇒tanA2tanB2+tanB2tanC2+tanC2tanA2=1
Bài toán được chứng minh.

Các bài tập cùng chuyên đề
Bài 1 :
Chọn đẳng thức đúng trong các đẳng thức sau:
-
A.
sin(a+b)=sin(a)cos(b)+cos(a)sin(b)
-
B.
sin(a+b)=sin(a)cos(a)+cos(b)sin(b)
-
C.
sin(a−b)=sin(a)cos(a)−cos(b)sin(b)
-
D.
sin(a−b)=sin(b)cos(a)−cos(a)sin(b)
Bài 2 :
Giải bài toán trong tình huống mở đầu:
Một thiết bị trễ kỹ thuật số lặp lại tín hiệu đầu vào bằng cách lặp lại tín hiệu đó trong một khoảng thời gian cố định sau khi nhận được tín hiệu. Nếu một thiết bị như vậy nhận được nốt thuần f1(t)=5sint và phát lại được nốt thuần f2(t)=5cost thì âm kết hợp là f(t)=f1(t)+f2(t), trong đó t là biến thời gian. Chứng tỏ rằng âm kết hợp viết được dưới dạng f(t)=ksin(t+φ), tức là âm kết hợp là một sóng âm hình sin. Hãy xác định biên độ âm k và pha ban đầu φ(−π<φ<π) của sóng âm.
Bài 3 :
Chứng minh rằng:
a) sinx−cosx=√2sin(x−π4);
b) tan(π4−x)=1−tanx1+tanx
(x≠π2+kπ,x≠3π4+kπ,k∈Z).
Bài 4 :
a) Cho a=π3 và b=π6, hãy chứng tỏ cos(a−b)=cosacosb+sinasinb.
b) Bằng cách viết a+b=a−(−b) và từ công thức ở HĐ1a, hãy tính cos(a+b).
c) Bằng cách viết sin(a−b)=cos[π2−(a−b)]=cos[(π2−a)+b]và sử dụng công thức vừa thiết lập ở HĐ1b, hãy tính sin(a−b).
Bài 5 :
Sử dụng 150=450−300, hãy tính các giá trị lượng giác của góc 150.
Bài 6 :
Tính:
a) cos(a+π6), biết sina=1√3 và π2<a<π;
b) tan(a−π4), biết cosa=−13 và π<a<3π2.
Bài 7 :
Chứng minh đẳng thức sau:
sin(a+b)sin(a−b)=sin2a−sin2b=cos2b−cos2a
Bài 8 :
Trong các khẳng định sau, khẳng định nào là sai?
A. cos(a−b)=cosacosb−sinasinb
B. sin(a−b)=sinacosb−cosasinb
C. cos(a+b)=cosacosb−sinasinb
D. sin(a+b)=sinacosb+cosasinb
Bài 9 :
Cho góc α thỏa mãn π2<α<π,cosα=−1√3. Tính giá trị của các biểu thức sau:
a) sin(α+π6);
b) cos(α+π6);
c) sin(α−π3);
d) cos(α−π6).
Bài 10 :
Tính tan165∘
Bài 11 :
a) Sử dụng công thức cộng đối với sin và côsin, hãy tính tan(a+b) theo tan a và tan b khi các biểu thức đều có nghĩa
b) Khi các biểu thức đều có nghĩa, hãy tính tan(a−b) bằng cách biến đổi tan(a−b)=tan[a+(−b)] và sử dụng công thức tan(a+b) có được ở câu a.
Bài 12 :
Tính cos15∘
Bài 13 :
a) Tính cos(a+b) bằng cách biến đổi cos(a+b)=sin[π2−(a+b)]=sin[(π2−a)−b] và sử dụng công thức cộng đối với sin
b) Tính cos(a−b) bằng cách biến đổi cos(a−b)=cos[a+(−b)] và sử dụng công thức cos(a+b) có được ở câu a
Bài 14 :
Tính sinπ12
Bài 15 :
a) Cho a=π6,b=π3. Hãy tính sina, cosa, sinb, cosb và sin(a + b). Từ đó rút ra đẳng thức sin(a + b) = sina cosb + cosa sinb (*).
b) Tính sin(a – b) bằng cách biến đổi sin(a – b) = sin[a + (‒b)] và sử dụng công thức (*).
Bài 16 :
Cho cosa=35 với 0<a<π2. Tính: sin(a+π6),cos(a−π3),tan(a+π4)
Bài 17 :
Tính
A=sin(a−17∘)cos(a+13∘)−sin(a+13∘)cos(a−17∘)
B=cos(b+π3)cos(π6−b)−sin(b+π3)sin(π6−b)
Bài 18 :
Tính sinπ12 và tanπ12
Bài 19 :
Quan sát Hình 1. Từ hai cách tính tích vô hướng của vectơ →OM,→ON sau đây:
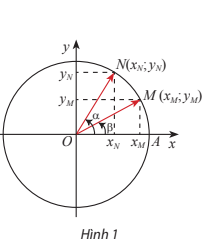
→OM.→ON=|→OM|.|→ON|.cos(→OM,→ON)=cos(→OM,→ON)=cos(α−β)
→OM.→ON=xM.xN+yM.yN
Hãy suy ra công thức tính cos(α – β) theo các giá trị lượng giác của α và β. Từ đó, hãy suy ra công thức cos(α + β) bằng cách thay β bằng – β.
Bài 20 :
Tính sin(α+π6),cos(π4−α) biết sinα=−513,π<α<3π2
Bài 21 :
Chứng minh rằng tam giác ABC, ta có sinA=sinB.cosC+sinC.cosB
Bài 22 :
Trong Hình 3, tam giác ABC vuông tại B và có hai cạnh góc vuông là AB = 4, BC = 3. Vẽ điểm D nằm trên tia đối của tia CB thỏa mãn ^CAD=300. Tính tan^BAD, từ đó tính độ dài cạnh CD.

Bài 23 :
Giá trị lượng giác sin(5π12) bằng?
-
A.
0,9
-
B.
√2(1+√3)2
-
C.
√3(1+√2)4
-
D.
√2(1+√3)4
Bài 24 :
Giá trị lượng giác cos(37π12) bằng?
-
A.
√6+√24
-
B.
√6−√24
-
C.
−√6+√24
-
D.
−√6−√24
Bài 25 :
Rút gọn biểu thức M=sin(x−y)cosy+cos(x−y)siny ta được
-
A.
M=cosx
-
B.
M=sinx
-
C.
M=sinxcos2y
-
D.
M=cosxcos2y
Bài 26 :
Không sử dụng máy tính, tính các giá trị lượng giác của góc 1050.
Bài 27 :
Chứng minh rằng
a) cosa−sina=√2cos(a+π4);
b) sina+√3cosa=2sin(a+π3).
Bài 28 :
Công thức nào sau đây đúng?
-
A.
cosα=−45
-
B.
tan(a+b)=tana+tanb
-
C.
sin(a−b)=sinacosb+cosasinb
-
D.
cos(a+b)=cosacosb−sinasinb
Bài 29 :
Cho hai góc a và b với tana=17 và tanb=34. Khi đó tan(a+b) bằng:
A. 1
B. −1731
C. 1731
D. −1
Bài 30 :
Nếu sinα=1√3 với 0<α<π2 thì giá trị của cos(α+π3) bằng:
A. √66−12
B. √6−3
C. √66−3
D. √6−12












