Nội dung từ Loigiaihay.Com
Cho đường thẳng a nằm trong mặt phẳng \(\left( \alpha \right)\) và đường thẳng b nằm trong mặt phẳng \(\left( \beta \right)\). Biết \(\left( \alpha \right)//\left( \beta \right)\). Trong các khẳng định sau, khẳng định nào sai?
A. a//\(\left( \beta \right)\).
B. b//\(\left( \alpha \right)\).
C. a//b.
D. Nếu có một mặt phẳng \(\left( \gamma \right)\) chứa a và b thì a//b.
Sử dụng kiến thức về hai mặt phẳng song song để tìm khẳng định sai: Nếu \(a \subset \left( \alpha \right),b \subset \left( \beta \right),\) \(\left( \alpha \right)//\left( \beta \right)\) thì a//b hoặc a và b chéo nhau.
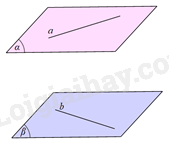
Nếu \(a \subset \left( \alpha \right),b \subset \left( \beta \right),\) \(\left( \alpha \right)//\left( \beta \right)\) thì a//b hoặc a và b chéo nhau nên C sai.
Chọn C

Các bài tập cùng chuyên đề
Bài 1 :
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N, P lần lượt là trung điểm của các cạnh AA’, BB’, CC’. Chứng minh rằng mặt phẳng (MNP) song song với mặt phẳng (ABC).
Bài 2 :
Trong mặt phẳng (P) cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn đường thẳng a, b, c, d đôi một song song với nhau và không nằm trong mặt phẳng (P). Một mặt phẳng cắt a, b, c, d lần lượt tại bốn điểm A’, B’, C’, D’. Chứng minh rằng A’B’C’D’ là hình bình hành.
Bài 3 :
Trong mặt phẳng \(\left( P \right)\) cho hình bình hành \(ABCD\). Ta dựng các nửa đường thẳng song song với nhau và nằm về một phía đối với \(\left( P \right)\) lần lượt đi qua các điểm \(A,B,C,D\). Một mặt phẳng \(\left( Q \right)\) cắt bốn nửa đường thẳng nói trên tại \(A',B',C',D'\). Chứng minh rằng:
\(AA' + CC' = BB' + DD'\).
Bài 4 :
Cho hình chóp \(S.ABCD\), đáy \(ABCD\) là hình bình hành có \(O\) là giao điểm của hai đường chéo. Gọi \(M,N\) lần lượt là trung điểm của \(SA,SD\).
a) Chứng minh rằng \(\left( {OMN} \right)\parallel \left( {SBC} \right)\).
b) Gọi \(E\) là trung điểm của \(AB\) và \(F\) là một điểm thuộc \(ON\). Chứng minh \(EF\) song song với \(\left( {SBC} \right)\).
Bài 5 :
Cho hai hình vuông \(ABCD\) và \(ABEF\) ở trong hai mặt phẳng khác nhau. Trên các đường chéo \(AC\) và \(BF\) lần lượt lấy các điểm \(M,N\) sao cho \(AM = BN\). Các đường thẳng song song với \(AB\) vẽ từ \(M,N\) lần lượt cắt \(AD,AF\) tại \(M',N'\).
a) Chứng minh \(\left( {CBE} \right)\parallel \left( {ADF} \right)\).
b) Chứng minh \(\left( {DEF} \right)\parallel \left( {MNN'M'} \right)\).
Bài 6 :
Cho hình hộp \(ABCD.A'B'C'D'\). Gọi \({G_1}\) và \({G_2}\) lần lượt là trọng tâm của hai tam giác \(BDA'\) và \(B'D'C\). Chứng minh \({G_1}\) và \({G_2}\) chia đoạn \(AC\) thành ba phần bằng nhau.
Bài 7 :
Để làm một khung lồng đèn kéo quân hình lăng trụ lục giác\(ABCDEF.A'B'C'D'E'F'\), Bình gắn hai thanh tre \({A_1}{D_1},{F_1}{C_1}\) song song với mặt phẳng đáy và cắt nhau tại \({O_1}\) (Hình 19).
a) Xác định giao tuyến của \(mp\left( {{A_1}{D_1},{F_1}{C_1}} \right)\) với các mặt bên của lăng trụ.
b) Cho biết \(A'{A_1} = 6A{A_1}\) và \(AA' = 70{\rm{ }}cm\). Tính \(C{C_1}\) và \({C_1}C'\).

Bài 8 :
-
A.
Hai đường thẳng không có điểm chung thì song song với nhau.
-
B.
Hai mặt phẳng phân biệt không song song thì cắt nhau.
-
C.
Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì song song với nhau.
-
D.
Hai đường thẳng chéo nhau thì không cùng thuộc một mặt phẳng.
Bài 9 :
Trong mặt phẳng \(\left( P \right)\) cho tam giác \(ABC\). Qua \(A,{\rm{ }}B,{\rm{ }}C\) lần lượt vẽ các tia \(Ax,{\rm{ }}By,{\rm{ }}Cz\) đôi một song song với nhau và không nằm trong mặt phẳng \(\left( P \right)\). Trên các tia \(Ax,{\rm{ }}By,{\rm{ }}Cz\) lần lượt lấy các điểm \(A',{\rm{ }}B',{\rm{ }}C'\) sao cho \(AA' = BB' = CC'\). Chứng minh rằng \(\left( {ABC} \right)\parallel \left( {A'B'C'} \right)\).
Bài 10 :
Cho hình chóp \(S.ABCD\) có đáy\(ABCD\) là hình thang với đáy lớn \(AD\). Gọi \(M\) là trọng tâm của tam giác \(SAD\), \(N\) là điểm thuộc đoạn thẳng \(AC\) sao cho \(AN = \frac{1}{3}AC\), \(P\) là điểm thuộc đoạn thẳng \(CD\) sao cho \(DP = \frac{1}{3}DC\). Chứng mình rằng \(\left( {MNP} \right)\parallel \left( {SBC} \right)\).
Bài 11 :
Cho hai hình bình hành \(ABCD\) và \(ABEF\) không cùng nằm trong một mặt phẳng. Trên các đường chéo \(AC\), \(BF\) lần lượt lấy các điểm \(M\), \(N\) sao cho \(\frac{{AM}}{{AC}} = \frac{{BN}}{{BF}}\). Qua \(M\) vẽ đường thẳng song song với \(AB\) cắt \(AD\) tại \(M'\), qua \(N\) vẽ đường thẳng song song với \(AB\) cắt \(AF\) tại \(N'\).
a) Chứng minh rằng \(\left( {MNN'} \right)\parallel \left( {CDE} \right)\).
b) Gọi \(\left( P \right)\) là mặt phẳng đi qua \(M\) và song song với mặt phẳng \(\left( {AFD} \right)\). Mặt phẳng \(\left( P \right)\) cắt đường thẳng \(EF\) tại \(I\). Tính \(\frac{{FI}}{{FE}}\), biết \(\frac{{AM}}{{AC}} = \frac{1}{3}\).
Bài 12 :
Cho mặt phẳng (P) và điểm A nằm ngoài mặt phẳng (P). Khẳng định nào sau đây là đúng?
A. Qua A có vô số mặt phẳng song song với (P)
B. Qua A có đúng một mặt phẳng song song với (P)
C. Qua A không có mặt phẳng song song với (P)
D. Qua A có đúng hai mặt phẳng song song với (P)
Bài 13 :
Cho hình hộp ABCD.A’B’C’D’. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AA’, BB’, CC’, DD’. Chứng minh rằng bốn điểm M, N, P, Q đồng phẳng và MNPQ là hình bình hành.
Bài 14 :
Cho hình hộp ABCD.A’B’C’D’. Chứng minh:
a) (BDA’)//(B’D’C).
b) Đường chéo AC’ đi qua trọng tâm G và G’ của hai tam giác BDA’ và B’D’C.
c) G và G’ chia AC’ thành ba phần bằng nhau.
Bài 15 :
Cho hình lăng trụ tam giác \(ABC.A'B'C'\). Gọi \(M,\,N\) lần lượt là trung điểm của \(A'B'\) và \(AB\).
a) Chứng minh \(CB'\,\,{\rm{//}}\,\left( {AMC'} \right)\).
b) Mặt phẳng \(\left( P \right)\) đi qua \(N\) song song với hai cạnh \(AB'\) và \(AC'\). Tìm giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( {BB'C'} \right)\).
Bài 16 :
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành có O là giao điểm của AC và BD, AC = 6, BD = 8; tam giác SBD là tam giác đều. Gọi I là điểm nằm trên đoạn thẳng AC sao cho AI = x (0 < x < 3), (P) là mặt phẳng đi qua điểm I và song song với mặt phẳng (SBD). Diện tích của hình tạo bởi các đoạn giao tuyến của mặt phẳng (P) với các mặt của hình chóp S.ABCD bằng \(\frac{{a{x^2}\sqrt 3 }}{b}\). Tính giá trị của biểu thức P = a + b.
Bài 17 :
Cho hình hộp $ABCD.A'B'C'D'$, gọi $G_{1},G_{2}$ là trọng tâm của các tam giác $A'BD$, $B'D'C$.
a) Chứng minh rằng: $\left( {A'BD} \right)\,\text{//}\,\left( {B'D'C} \right)$.
b) Chứng minh rằng $G_{1},G_{2}$ cùng thuộc $AC'$ và chia $AC'$ thành ba đoạn bằng nhau.












