Nội dung từ Loigiaihay.Com
Trong không gian Oxyz, cho ba điểm A(1;0;9), B(6;1;0) và C(0;0;1). Gọi G là trọng tâm của tam giác ABC. Tìm toạ độ điểm G.
Trọng tâm của tam giác là trung bình cộng tọa độ của ba đỉnh của tam giác. Nếu các đỉnh của tam giác là \(A({x_1},{y_1},{z_1})\), \(B({x_2},{y_2},{z_2})\), và \(C({x_3},{y_3},{z_3})\), tọa độ của trọng tâm G được tính bằng:
\(G\left( {\frac{{{x_1} + {x_2} + {x_3}}}{3},\frac{{{y_1} + {y_2} + {y_3}}}{3},\frac{{{z_1} + {z_2} + {z_3}}}{3}} \right)\)

Toạ độ của điểm trọng tâm G là trung bình cộng của toạ độ các điểm A, B, C.
\({x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{1 + 6 + 0}}{3} = \frac{7}{3}\)
\({y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{0 + 1 + 0}}{3} = \frac{1}{3}\)
\({z_G} = \frac{{{z_A} + {z_B} + {z_C}}}{3} = \frac{{9 + 0 + 1}}{3} = \frac{{10}}{3}\)
Toạ độ của trọng tâm G là: \(G\left( {\frac{7}{3},\frac{1}{3},\frac{{10}}{3}} \right)\)

Các bài tập cùng chuyên đề
Bài 1 :
Trong không gian Oxyz, cho ba điểm \(A\left( {2;9; - 1} \right),B\left( {9;4;5} \right)\) và \(G\left( {3;0;4} \right)\). Tìm tọa độ điểm C sao cho tam giác ABC nhận G là trọng tâm.
Bài 2 :
Trong không gian Oxyz, cho tam giác ABC có \(A\left( {{x_A};{y_A};{z_A}} \right),B\left( {{x_B};{y_B};{z_B}} \right)\) và \(C\left( {{x_C};{y_C};{z_C}} \right)\).
a) Gọi M là trung điểm của đoạn thẳng AB. Tìm tọa độ của M theo tọa độ của A và B.
b) Gọi G là trọng tâm của tam giác ABC. Tìm tọa độ của G theo tọa độ của A và B và C.
Bài 3 :
Trong không gian Oxyz, cho \(A\left( {1;0; - 1} \right),B\left( {0; - 1;2} \right)\) và \(G\left( {2;1;0} \right)\). Biết tam giác ABC có trọng tâm G. Tọa độ của điểm C là
A. \(\left( {5;4; - 1} \right)\).
B. \(\left( { - 5; - 4;1} \right)\).
C. \(\left( {1;2; - 1} \right)\).
D. \(\left( { - 1; - 2;1} \right)\)
Bài 4 :
a) Trong không gian với hệ tọa độ Oxyz, cho hai điểm \(A({x_A};{y_A};{z_A})\) và \(B({x_B};{y_B};{z_B})\). Gọi \(M({x_M};{y_M};{z_M})\)là trung điểm đoạn thẳng AB
- Biểu diễn vecto \(\overrightarrow {OM} \) theo hai vecto \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \)
- Tính tọa độ của điểm M theo tọa độ của các điểm \(A({x_A};{y_A};{z_A})\) và \(B({x_B};{y_B};{z_B})\)
b) Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có trọng tâm G
- Biểu diễn vecto \(\overrightarrow {OG} \) theo ba vecto \(\overrightarrow {OA} \), \(\overrightarrow {OB} \) và \(\overrightarrow {OC} \)
- Tính tọa độ của điểm G theo tọa độ của các điểm \(A({x_A};{y_A};{z_A})\), \(B({x_B};{y_B};{z_B})\) và \(C({x_C};{y_C};{z_C})\)
Bài 5 :
Cho hai điểm M(1;-2;3) và N(3;4;-5). Trung điểm của đoạn thẳng MN có tọa độ là:
A. (-2;1;1)
B (2;1;1)
C. (-2;1;-1)
D. (2;1;-1)
Bài 6 :
Cho tam giác MNP có M(0;2;1), N(-1;-2;3) và P(1;3;2). Trọng tâm của tam giác MNP có tọa độ là:
A. (0;1;2)
B. (0;3;6)
C. (0;-3;-6)
D. (0;-1;-2)
Bài 7 :
Xét hệ tọa độ Oxyz gắn với hình lập phương ABCD.A’B’C’D’ như Hình 39, đơn vị của mỗi trục bằng độ dài cạnh hình lập phương. Biết A(0;0;0), B(1;0;0), D(0;1;0), A’(0;0;1).
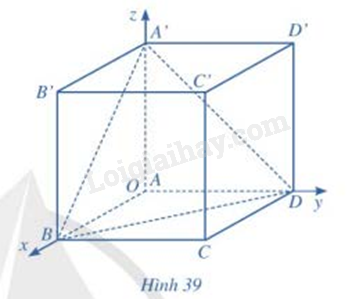
a) Xác định tọa độ các đỉnh còn lại của hình lập phương ABCD.A’B’C’D’
b) Xác định tọa độ trọng tâm G của tam giác A’BD
c) Xác định tọa độ các vecto \(\overrightarrow {OG} \) và \(\overrightarrow {OC'} \). Chứng minh rằng ba điểm O, G, C’ thẳng hàng và \(OG = \frac{1}{3}OC\)
Bài 8 :
Trên phần mềm mô phỏng việc điều khiển drone giao hàng trong không gian Oxyz, một đội gồm ba drone giao hàng A, B, C đang có toạ độ là A(1; 1; 1), B(5; 7; 9), C(9; 11 ; 4). Tính:
a) Các khoảng cách giữa mỗi cặp drone giao hàng.
b) Góc \(\widehat {BAC}\)
Bài 9 :
Cho tam giác MNP có M(0; 1; 2), N(5; 9; 3), P(7; 8; 2).
a) Tìm toạ độ điểm K là chân đường cao kẻ từ M của tam giác MNP.
b) Tìm độ dài cạnh MN và MP.
c) Tính góc M
Bài 10 :
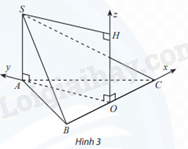
Cho hình chóp S.ABC có \(SA \bot (ABC)\), SA = a và đáy ABC là tam giác đều cạnh a, O là trung điểm của BC. Bằng cách thiết lập hệ toạ độ như hình vẽ, hãy tìm toạ độ:
a) Các điểm A, S, B, C
b) Trung điểm M của SB và trung điểm N của SC;
c) Trọng tâm G của tam giác SBC
Bài 11 :
Cho tam giác MNP có M(2; 1; 3), N(1; 2; 3), P(–3; –1; 0). Tìm toạ độ:
a) Các điểm M′, N′, P′ lần lượt là trung điểm của các cạnh NP, MP, MN;
b) Trọng tâm G của tam giác M′N′P′.
Bài 12 :
Cho tam giác ABC có \(A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B}),C({x_C};{y_C};{z_C})\). Gọi \(M({x_M};{y_M};{z_M})\) là trung điểm của đoạn thẳng AB và \(G({x_G};{y_G};{z_G})\) là trọng tâm của tam giác ABC. Sử dụng các hệ thức vectơ \(\overrightarrow {OM} = \frac{1}{2}(\overrightarrow {OA} + \overrightarrow {OB} )\),\(\overrightarrow {OG} = \frac{1}{3}(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} )\), tìm toạ độ của các điểm M và G.
Bài 13 :
Cho ba điểm A(2; 1; –1), B(3; 2; 0) và C(2; –1; 3).
a) Chứng minh rằng A, B, C là ba đỉnh của một tam giác. Tính chu vi tam giác ABC.
b) Tìm toạ độ trung điểm của các cạnh của tam giác ABC.
c) Tìm toạ độ trọng tâm G của tam giác ABC.
Bài 14 :
Cho điểm M(1; 2; 3). Hãy tìm toạ độ của các điểm:
a) \({M_1},{M_2},{M_3}\) lần lượt là hình chiếu vuông góc của M trên các mặt phẳng toạ độ (Oxy), (Oyz), (Oxz).
b)
b) Gọi M', M", M"' lần lượt là các điểm thỏa mãn:
+ O là trung điểm của MM';
+ MM" vuông góc với mặt phẳng (Oxy) tại điểm H sao cho H là trung điểm của MM";
+ MM"' vuông góc và cắt trục Oy tại điểm K sao cho K là trung điểm của MM"'.
Bài 15 :
Cho ba điểm A(3;3;3), B(1;1;2) và C(5;3;1).
a) Tìm điểm M trên trục Oy cách đều hai điểm B, C.
b) Tìm điểm N trên mặt phẳng (Oxy) cách đều ba điểm A, B, C.
Bài 16 :
Cho hai điểm A(3; –2; 3) và B(–1; 2; 5). Toạ độ trung điểm I của đoạn thẳng AB là
A. I(–2; 2; 1).
B. I(1; 0; 4).
C. I(2; 0; 8).
D. I(2; –2; –1)
Bài 17 :
Cho ba điểm A(1; 3; 5), B(2; 0; 1), C(0; 9; 0). Toạ độ trọng tâm G của tam giác ABC là
A. G(3; 12; 6).
B. G(1; 5; 2).
C. G(1; 0; 5).
D. G(1; 4; 2).
Bài 18 :
Cho ba điểm A(0; 2; -1), B(-5; 4; 2), C(-1; 0; 5). Tìm tọa độ trọng tâm G của tam giác ABC.
Bài 19 :
Cho sáu điểm \(A\left( {1;2;3} \right),B\left( {2; - 1;1} \right),C\left( {3;3; - 3} \right)\) và \(A',B',C'\) thoả mãn \(\overrightarrow {A'A} + \overrightarrow {B'B} + \overrightarrow {C'C} = \overrightarrow 0 \). Tìm toạ độ trọng tâm \(G\) của tam giác \(A'B'C'\).
Bài 20 :
Cho tam giác \(ABC\) có đỉnh \(C\left( { - 2;2;2} \right)\) và trọng tâm \(G\left( { - 1;1;2} \right)\). Tìm toạ độ các đỉnh \(A,B\) của tam giác \(ABC\), biết điểm \(A\) thuộc mặt phẳng \(\left( {Oxy} \right)\) và điểm \(B\) thuộc \(Oz\).
Bài 21 :
Cho tứ diện \(ABCD\). Lấy \(G\) là trọng tâm tam giác \(BCD\). Phát biểu nào sau đây là sai?
A. \(\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \)
B. \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \)
C. \(\overrightarrow {CB} + \overrightarrow {CD} = 3\overrightarrow {CG} \)
D. \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AG} \).
Bài 22 :
Cho hai điểm \(A\left( {2;2; - 1} \right)\) và \(B\left( {4;6; - 3} \right)\). Toạ độ trung điểm \(M\) của đoạn thẳng \(AB\) là:
A. \(\left( {3;4; - 2} \right)\)
B. \(\left( {6;8; - 4} \right)\)
C. \(\left( {1;2; - 1} \right)\)
D. \(\left( { - 1; - 2;1} \right)\)
Bài 23 :
Cho tam giác \(ABC\) có \(A\left( {1;3;2} \right),B\left( {2; - 1;1} \right)\) và \(C\left( {3;1;0} \right)\). Toạ độ trọng tâm \(G\) của tam giác \(ABC\) là:
A. \(\left( {6;3;3} \right)\)
B. \(\left( {2;1;1} \right)\)
C. \(\left( {3;\frac{3}{2};\frac{3}{2}} \right)\)
D. \(\left( {2;\frac{5}{3};1} \right)\)
Bài 24 :
Cho hai điểm \(M\left( {5;2; - 3} \right)\) và \(N\left( {1; - 4;5} \right)\). Trung điểm của đoạn thẳng \(MN\) có toạ độ là:
A. \(\left( {4;6; - 8} \right)\)
B. \(\left( {2;3; - 4} \right)\)
C. \(\left( {6; - 2;2} \right)\)
D. \(\left( {3; - 1;1} \right)\)
Bài 25 :
Cho tam giác \(MNP\) có \(M\left( {1; - 2;1} \right),N\left( { - 1; - 2;3} \right)\) và \(P\left( {3;1;2} \right)\). Trọng tâm của tam giác \(MNP\) có toạ độ là:
A. \(\left( {1; - 1;2} \right)\)
B. \(\left( {3; - 3;6} \right)\)
C. \(\left( { - 1;1; - 2} \right)\)
D. \(\left( { - 3;3; - 6} \right)\)
Bài 26 :
Trong không gian \(Oxyz\), cho tứ diện \(ABCD\) với \(A\left( {1;3; - 3} \right)\), \(B\left( {2;0;5} \right)\), \(C\left( {6;9; - 5} \right)\) và
\(D\left( { - 1; - 4;3} \right)\).
a) Tìm tọa độ trọng tâm \(I\) của tam giác \(ABC\).
b) Tìm tọa độ của điểm \(G\) thuộc đoạn thẳng \(DI\) sao cho\(DG = 3IG\).
Bài 27 :
Cho tứ diện \(ABCD\). Trọng tâm \(G\) của tứ diện là điểm duy nhất thỏa mãn đẳng thức
\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \). Chứng minh rằng tọa độ của điểm \(G\) được cho bởi công thức:
\({x_G} = \frac{{{x_A} + {x_B} + {x_C} + {x_D}}}{4};{y_G} = \frac{{{y_A} + {y_B} + {y_C} + {y_D}}}{4};{z_G} = \frac{{{z_A} + {z_B} + {z_C} + {z_D}}}{4}.\)
Bài 28 :
Trong không gian \(Oxyz\), cho ba điểm \(A\left( {1;3;5} \right)\), \(B\left( {0;6; - 2} \right)\), \(C\left( {5;3;6} \right)\). Tọa độ trọng tâm của tam giác \(ABC\) là
A. \(\left( {2;3;4} \right)\)
B. \(\left( {2;4;3} \right)\)
C. \(\left( {3;4;2} \right)\)
D. \(\left( {3;2;4} \right)\)
Bài 29 :
Trong không gian Oxyz, cho ba điểm \(A(1;3; - 5)\), \(M\left( {\frac{3}{2};2; - \frac{1}{2}} \right)\), \(G\left( {2;\frac{2}{3}; - \frac{2}{3}} \right)\).
a) Tìm tọa độ điểm B sao cho M là trung điểm của đoạn thẳng AB.
b) Tìm tọa độ điểm C sao cho G là trọng tâm của tam giác ABC.
Bài 30 :
Trong không gian Oxyz, tam giác ABC có \(A\left( {{x_A},{y_A},{z_A}} \right)\), \(B\left( {{x_B},{y_B},{z_B}} \right)\), và \(C\left( {{x_C},{y_C},{z_C}} \right)\)
a) Gọi M là trung điểm của đoạn thẳng A B. Tìm tọa độ điểm M.
b) Gọi G là trọng tâm tam giác ABC. Tìm tọa độ điểm G.












