Nội dung từ Loigiaihay.Com
Cho hình bình hành ABCD. Gọi M, N, P lần lượt là trung điểm của các đoạn thẳng AB, BC, AN và Q là giao điểm của AN và DM. Chứng minh:
a) \(MP\parallel AD,\,\,MP = \frac{1}{4}AD\)
b) \(AQ = \frac{2}{5}AN\)
c) Gọi R là trung điểm của CD. Chứng minh ba điểm M, P, R thẳng hàng và \(PR = \frac{3}{4}AD\).
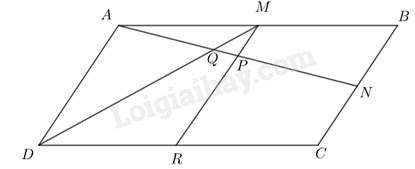
a) Chứng minh MP là đường trung bình của tam giác ABN.
b) Từ \(MP\parallel AD\), sử dụng định lý Thales để chứng minh đẳng thức.
c) Chứng minh \(MR\parallel AD\) và sử dụng các tỉ lệ đã có để chứng minh yêu cầu đề bài.

Vì M và P lần lượt là trung điểm của AB và AN nên MP là đường trung bình của tam giác ABN.
\( \Rightarrow MP\parallel BN\) hay \(MP\parallel BC\).
Mà ABCD là hình bình hành nên \(AD\parallel BC\)
\( \Rightarrow MP\parallel AD\)
Ta có: \(MP = \frac{1}{2}NB\)
Mà N là trung điểm BC nên \(NB = \frac{1}{2}BC\)
\( \Rightarrow MP = \frac{1}{4}BC \Rightarrow MP = \frac{1}{4}AD\)
b) Vì \(MP\parallel AD\) nên \(\frac{{MP}}{{AD}} = \frac{{QP}}{{AQ}}\) (hệ quả của định lý Thales)
\( \Rightarrow \frac{{QP}}{{AQ}} = \frac{1}{4} \Rightarrow AQ = 4QP\,\,\left( 1 \right)\)
Ta có: \(QP = AP - AQ = \frac{1}{2}AN - AQ\) (P là trung điểm AN)
Thay vào (1) ta được \(AQ = 4.\left( {\frac{1}{2}AN - AQ} \right)\)
\( \Rightarrow AQ = 2AN - 4AQ \Rightarrow 5AQ = 2AN \Rightarrow AQ = \frac{2}{5}AN\) (đpcm)
c) Vì M và R lần lượt là trung điểm của AB và CD nên \(MR\parallel AD,\,\,MR = AD\)
Mà ta đã chứng minh \(MP\parallel AD\) nên ba điểm M, P, R thẳng hàng.
Theo câu a) ta có \(MP = \frac{1}{4}AD \Rightarrow MP = \frac{1}{4}MR\)
\( \Rightarrow PR = \frac{3}{4}MR \Rightarrow PR = \frac{3}{4}AD\).

Các bài tập cùng chuyên đề
Bài 1 :
Cho tam giác ABC, các đường trung tuyến BD, CE. Gọi M, N theo thứ tự là trung điểm của BE, CD. Gọi I, K theo thứ tự là giao điểm của MN với BD và CE. Chứng minh \(MI = IK = KN\).
Bài 2 :
Cho hình bình hành ABCD, AC cắt BD tại O. Đường phân giác góc A cắt BD tại M, đường phân giác góc D cắt AC tại N. Chứng minh MN//AD.
Bài 3 :
Cho \(\Delta ABC\) cân tại A, trung tuyến AM. Gọi I là trung điểm của AC. Trên tia MI lấy điểm N sao cho I là trung điểm của MN.
a) Tứ giác AMCN là hình gì? Vì sao?
b) Gọi E là trung điểm của AM. Chứng minh E là trung điểm của BN.
c) Gọi K là trung điểm của AB. Tìm điều kiện để AKMI là hình vuông.
Bài 4 :
a) Cho tam giác ABC có AB = 6 cm, AC = 8 cm. Đường phân giác của góc A cắt BC tại D. Biết DB = 3 cm. Tính DC.
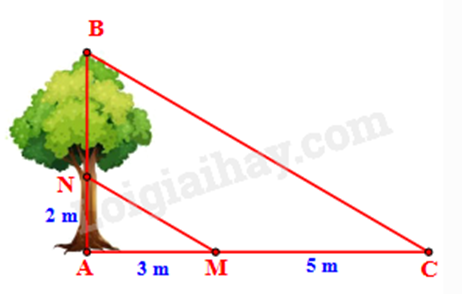
b) Độ cao AN và chiều dài bóng nắng của các đoạn thẳng AN, BN trên mặt đất được ghi lại như trong hình vẽ bên. Tìm chiều cao AB của cây.
Bài 5 :
Cho tam giác ABC, trung tuyến AM. Các tia phân giác của góc AMB, AMC cắt AB, AC lần lượt tại D và E. Cho BC = 12cm, AM = 8cm, AB = 7cm. Gọi I là giao điểm của DE và AM.
a) \(\frac{{AD}}{{DB}} = \frac{2}{3}\).
b) \(DE//BC\)
c) \(DE = \frac{{36}}{7}\).
d) \(DI = IE\)












