Nội dung từ Loigiaihay.Com
Một phân xưởng có hai loại máy chuyên dụng \({M_1}\) và \({M_2}\) để sản xuất hai loại sản phẩm A và B theo đơn đặt hàng. Nếu sản xuất được một tấn sản phẩm loại A thì phân xưởng nhận được số tiền lãi là 2 triệu đồng. Nếu sản xuất được một tấn sản phẩm loại B thì phân xưởng nhận được số tiền lãi là 1,6 triệu đồng. Muốn sản xuất một tấn sản phẩm loại A, người ta phải dùng máy \({M_1}\) trong 3 giờ và máy \({M_2}\) trong 1 giờ. Muốn sản xuất một tấn sản phẩm loại B, người ta phải dùng máy \({M_1}\) trong 1 giờ và máy \({M_2}\) trong 1 giờ. Một máy không thể dùng sản xuất đồng thời hai loại sản phẩm. Máy \({M_1}\) làm việc không quá 6 giờ một ngày và máy \({M_2}\) làm việc không quá 4 giờ một ngày. Hỏi số tiền lãi lớn nhất mà phân xưởng này có thể thu được trong một ngày là bao nhiêu?
- Viết hệ bất phương trình của bài toán nói trên
- Xác định miền nghiệm của hệ bất phương trình
- Viết biểu thức biểu thị số tiền lại phân xưởng thu được đạt giá trị lớn nhất
- Gọi \(x\) và \(y\) là số tấn sản phẩm loại A và loại B mà phân xưởng sản xuất được.
Điều kiện: \(x \ge 0;\,\,y \ge 0.\)
Thời gian máy \({M_1}\) làm việc không quá 6 giờ một ngày là: \(3x + y \le 6.\)
Thời gian máy \({M_2}\) làm việc không quá 4 giờ một ngày là: \(x + y \le 4.\)
Ta có hệ bất phương trình: \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{3x + y \le 6}\\{x + y \le 4}\end{array}.} \right.\)
Số tiền lãi phân xưởng này thu được trong một ngày là: \(F\left( {x;y} \right) = 2x + 1,6y \to \max \)
- Xác định miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{3x + y \le 6}\\{x + y \le 4}\end{array}.} \right.\)
Miền nghiệm của bất phương trình \(d:x \ge 0\) là nửa mặt phẳng bờ \(d\) chứa điểm \(\left( {1;0} \right).\)
Miền nghiệm của bất phương trình \({d_1}:y \ge 0\) là nửa mặt phẳng bờ \({d_1}\) chứa điểm \(\left( {0;1} \right).\)
Miền nghiệm của bất phương trình \(3x + y \le 6\) là nửa mặt phẳng bờ \({d_2}:3x + y = 6\) chứa gốc tọa độ \(O\left( {0;0} \right).\)
Miền nghiệm của bất phương trình \(x + y \le 4\) là nửa mặt phẳng bờ \({d_3}:x + y = 4\) chứa gốc tọa độ \(O\left( {0;0} \right).\)
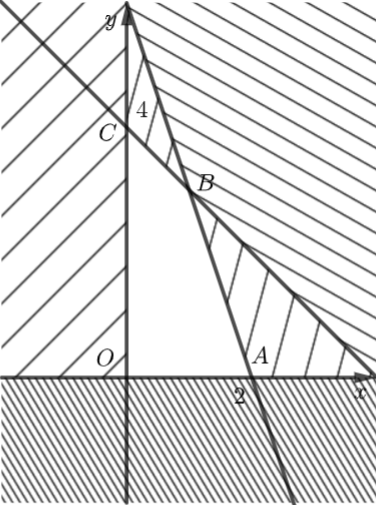
Miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{3x + y \le 6}\\{x + y \le 4}\end{array}} \right.\) là tứ giác \(OABC\) với \(A\left( {2;0} \right),\) \(B\left( {1;3} \right),\,\,C\left( {0;4} \right).\)
- Ta có: \(F\left( {2;0} \right) = 2.2 + 1,6.0 = 4;\,\,F\left( {0;0} \right) = 2.0 + 1,6.0 = 0;\)
\(F\left( {1;3} \right) = 2.1 + 1,6.3 = 6,8;\) \(F\left( {0;4} \right) = 2.0 + 1,6.4 = 6,4.\)
Vậy số tiền lãi lớn nhất phân xưởng này thu được trong một ngày là: 6,8 triệu đồng.

Các bài tập cùng chuyên đề
Bài 1 :
Bạn An kinh doanh hai mặt hàng handmade là vòng tay và vòng đeo cổ. Mỗi vòng tay làm trong 4 giờ, bán được 40 ngàn đồng. Mỗi vòng đeo cổ làm trong 6 giờ, bán được 80 ngàn đồng. Mỗi tuần bạn An bán được không quá 15 vòng tay và 4 vòng đeo cổ. Tính số giờ tối thiểu trong tuần An cần dùng để bán được ít nhất 400 ngàn đồng?
-
A.
32 giờ
-
B.
84 giờ
-
C.
60 giờ
-
D.
40 giờ
Bài 2 :
Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24 g hương liệu, 9 lít nước và 210 g đường để pha chế nước cam và nước táo.
- Để pha chế 1 lít nước cam cần 30 g đường, 1 lít nước và 1 g hương liệu;
- Để pha chế 1 lít nước táo cần 10 g đường, 1 lít nước và 4 g hương liệu.
Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để đạt được số điểm thưởng cao nhất?
-
A.
5 lít nước cam và 4 lít nước táo.
-
B.
6 lít nước cam và 5 lít nước táo.
-
C.
4 lít nước cam và 5 lít nước táo.
-
D.
4 lít nước cam và 6 lít nước táo.
Bài 3 :
Một cửa hàng có kế hoạch nhập về hai loại máy tính A và B, giá mỗi chiếc lần lượt là 10 triệu đồng và 20 triệu đồng với số vốn ban đầu không vượt quá 4 tỉ đồng. Loại máy A mang lại lợi nhuận 2,5 triệu đồng cho mỗi máy bán được và loại máy B mang lại lợi nhuận là 4 triệu đồng mỗi máy. Cửa hàng ước tính rằng tổng nhu cầu hàng tháng sẽ không vượt quá 250 máy. Giả sử trong một tháng cửa hàng cần nhập số máy tính loại A là x và số máy tính loại B là y.
a) Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương
trình rồi xác định miền nghiệm của hệ đó.
b) Gọi F (triệu đồng) là lợi nhuận mà cửa hàng thu được trong tháng đó khi bán x máy tính loại A và y máy tính loại B. Hãy biểu diễn F theo x và y.
c) Tìm số lượng máy tính mỗi loại cửa hàng cần nhập về trong tháng đó đề lợi nhuận thu được là lớn nhất.
Bài 4 :
Xét biểu thức F(x, y) = 2x + 3y với (x; y) thuộc miền tam giác OAB ở HĐ2. Toạ độ ba đình là O(0, 0), A(150, 0) và B(0; 150) (H.2.5).
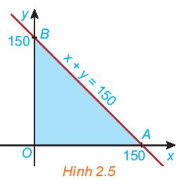
a) Tính giá trị của biểu thức F(x; y) tại mỗi đỉnh O, A và B.
b) Nêu nhận xét về dấu của hoành độ x và tung độ y của điểm (x; y) nằm trong miền tam giác OAB. Từ đó suy ra giá trị nhỏ nhất của F(x; y) trên miền tam giác OAB.
c) Nêu nhận xét về tổng x + y của điểm (X; y) nằm trong miền tam giác OAB. Từ đó suy ra giá trị lớn nhất của F(x, y) trên miền tam giác OAB.
Bài 5 :
c) Tìm số kilôgam thịt mỗi loại mà gia đình cần mua để chi phí là ít nhất.
Bài 6 :
b) Gọi F (nghìn đồng) là số tiền phải trả cho x kilôgam thịt bò và y kilôgam thịt lợn. Hãy
biểu diễn F theo x và y.
Bài 7 :
a) Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương
trình rồi xác định miền nghiệm của hệ đó.
Bài 8 :
Bác An đầu tư 1,2 tỉ đồng vào ba loại trái phiếu, trái phiếu chính phủ với lãi suất 7% một năm, trái phiếu ngân hàng với lãi suất 8% một năm và trái phiếu doanh nghiệp rủi ro cao với lãi suất 12% một năm. Vì lí do giảm thuế, bác An muốn số tiền đầu tư trái phiếu chính phủ gấp ít nhất 3 lần số tiền đầu tư trái phiếu ngân hàng. Hơn nữa, để giảm thiểu rủi ro, bác An đầu tư không quá 200 triệu đồng cho trái phiếu doanh nghiệp. Hỏi bác An nên đầu tư mỗi loại trái phiếu bao nhiêu tiền để lợi nhuận thu được sau một năm là lớn nhất?
Bài 9 :
Một công ty dự định chi tối đa 160 triệu đồng cho quảng cáo một sản phẩm mới trong một tháng trên các đài phát thanh và truyền hình. Biết cùng một thời lượng quảng cáo, số người mới quan tâm đến sản phẩm trên truyền hình gấp 8 lần trên đài phát thanh, tức là quảng cáo trên truyền hình có hiệu quả gấp 8 lần trên đài phát thanh.
Đài phát thanh chỉ nhận các quảng cáo có tổng thời lượng trong một tháng tối đa là 900 giây với chi phí là 80 nghìn đồng/giây. Đài truyền hình chỉ nhận các quảng cáo có tổng thời lượng trong một tháng tối đa là 360 giây với chi phí là 400 nghìn đồng/giây.
Công ty cần đặt thời gian quảng cáo trên các đài phát thanh và truyền hình như thế nào để hiệu quả nhất?
Gợi ý. Nếu coi hiệu quả khi quảng cáo 1 giây trên đài phát thanh là 1 (đơn vị) thì hiệu quả khi quảng cáo 1 giây trên đài truyền hình là 8 (đơn vị). Khi đó hiệu quả quảng cáo x (giây) trên đài phát thanh và y (giây) trên truyền hình là F(x, y) = x + 8y. Ta cần tìm giá trị lớn nhất của hàm F(x, y) với x, y thoả mãn các điều kiện trong đề bài.
Bài 10 :
Trong năm nay, một cửa hàng điện lạnh dự định kinh doanh hai loại máy điều hoà điều hoà hai chiều và điều hoà một chiều với số vốn ban đầu không vượt quá 1,2 tỷ đồng.
|
|
Điều hòa hai chiều |
Điều hòa một chiều |
|
Giá mua vào |
20 triệu đồng/1 máy |
10 triệu đồng/1 máy |
|
Lợi nhuận dự kiến |
3,5 triệu đồng/1 máy |
2 triệu đồng/1 máy |
Cửa hàng ước tính rằng tổng nhu cầu của thị trường sẽ không vượt quá 100 máy cả hai loại. Nếu là chủ cửa hàng thì em cần đầu tư kinh doanh mỗi loại bao nhiêu máy đề lợi nhuận thu được là lớn nhất?
Bài 11 :
Một phân xưởng sản xuất hai kiểu mũ. Thời gian để làm ra một chiếc mũ kiểu thứ nhất nhiều gấp hai lần thời gian làm ra một chiếc mũ kiểu thứ hai. Nếu chỉ sản xuất toàn kiểu mũ thứ hai thì trong 1 giờ phân xưởng làm được 60 chiếc. Phân xưởng làm việc 8 tiếng mỗi ngày và thị trường tiêu thụ tối đa trong một ngày là 200 chiếc mũ kiểu thứ nhất và 240 chiếc mũ kiểu thứ hai. Tiền lãi khi bán một chiếc mũ kiểu thứ nhất là 24 nghìn đồng, một chiếc mũ kiểu thứ hai là 15 nghìn đồng. Tính số lượng mũ kiểu thứ nhất và kiểu thứ hai trong một ngày mà phân xưởng cần sản xuất để tiền lãi thu được là cao nhất.
Bài 12 :
Quảng cáo sản phẩm trên truyển hình là một hoạt động quan trong trong kinh doanh của các doanh nghiêp. Theo Thông báo số 10/2019, giá quảng cáo trên VTV1 là 30 triệu đồng cho 15 giây/1 lần quảng cáo vào khoảng 20h30; là 6 triệu đồng cho 15 giây/1 lần quảng cáo vào khung giờ 16h00 - 17h00. Môt công ty dự định chi không quá 900 triệu đồng để quảng cáo trên VTV1 với yêu cầu quảng cáo về số lần phát như sau: ít nhất 10 lần quảng cáo vào khoảng 20h30 và không quá 50 lần quảng cáo vào khung giờ 16h00 - 17h00. Gọi x, y lần luợt là số lần phát quảng cáo vào khoảng 20h30 và vào khung giờ 16h00 - 17h00.
Trong toán học, các điều kiện ràng buộc đối với x và y để đáp ứng nhu cầu trên của công ty đuợc thể hiện như thế nào?
Bài 13 :
Một người bán nước giải khát đang có 24 g bột cam, 9 l nước và 210 g đường để pha chế hai loại nước cam A và B. Để pha chế 1 l nước cam loại A cần 30 g đường, 1 l nước và 1 g bột cam; để pha chế 1 l nước cam loại B cần 10 g đường, 1 l nước và 4 g bột cam. Mỗi lít nước cam loại A bán được 60 nghìn đồng, mỗi lít nước cam loại B bán được 80 nghìn đồng. Người đó nên pha chế bao nhiêu lít nước cam mỗi loại để có doanh thu cao nhất?
Bài 14 :
Một nhà máy sản xuất hai loại thuốc trừ sâu nông nghiệp là A và B. Cứ sản xuất mỗi thùng loại A thì nhà máy thải ra 0,25 kg khí carbon dioxide (\(C{O_2}\)) và 0,60 kg khí sulful dioxide (\(S{O_2}\)), sản xuất mỗi thùng loại B thì thải ra 0,50 kg \(C{O_2}\) và 0,20 kg \(S{O_2}\). Biết rằng, quy định hạn chế sản lượng \(C{O_2}\) của nhà máy tối đa là 75 kg và \(S{O_2}\)tối đa là 90 kg mỗi ngày.
a) Tìm hệ bất phương trình mô tả số thùng của mỗi loại thuốc trừ sâu mà nhà máy có thể sản xuất mỗi ngày để đáp ứng các điều kiện hạn chế trên. Biểu diễn miền nghiệm của hệ bất phương trình đó trên mặt phẳng toạ độ.
b) Việc nhà máy sản xuất 100 thùng loại A và 80 thùng loại B mỗi ngày có phù hợp với quy định không?
c) Việc nhà máy sản xuất 60 thùng loại A và 160 thùng loại B mỗi ngày có phù hợp với quy định không?
Bài 15 :
Bạn Lan thu xếp được không quá 10 giờ để làm hai loại đèn trung thu tặng cho các trẻ em khuyết tật. Loại đèn hình con cá cần 2 giờ để làm xong 1 cái, còn loại đèn ông sao chỉ cần 1 giờ để làm xong 1 cái. Gọi x, y lần lượt là số đèn hình con cá và đèn ông sao bạn Lan sẽ làm. Hãy lập hệ bất phương trình mô tả điều kiện của x, y và biểu diễn miền nghiệm của hệ bất phương trình đó.
Bài 16 :
Một học sinh dự định vẽ các tấm thiệp xuân làm bằng tay để bán trong một hội chợ Tết. Cần 2 giờ để vẽ một tấm thiệp loại nhỏ có giá 10 nghìn đồng và 3 giờ để vẽ một tấm thiệp loại lớn có giá 20 nghìn đồng. Học sinh này chỉ có 30 giờ để vẽ và ban tổ chức hội chợ yêu cầu phải vẽ ít nhất 12 tấm. Hãy cho biết bạn ấy cần vẽ bao nhiêu tấm thiệp mỗi loại để có được nhiều tiền nhất.
Bài 17 :
Trong một tuần, bạn Mạnh có thể thu xếp được tối đa 12 giờ để tập thể dục giảm cân bằng hai môn: đạp xe và tập cử tạ tại phòng tập. Cho biết mỗi giờ đạp xe sẽ tiêu hao 350 calo và không tốn chi phí, mỗi giờ tập cử tạ sẽ tiêu hao 700 calo với chi phí 50 000 đồng/giờ. Mạnh muốn tiêu hao nhiều calo nhưng không được vượt quá 7 000 calo một tuần. Hãy giúp bạn Mạnh tính số giờ đạp xe và số giờ tập tạ một tuần trong hai trường hợp sau:
a) Mạnh muốn chi phí luyện tập là ít nhất.
b) Mạnh muốn số calo tiêu hao là nhiều nhất.
Bài 18 :
Nhà cô Minh có mảnh vườn rộng \(8{m^2}\). Cô dự định trồng cà chua và cải bắp trên toàn bộ mảnh vườn đó. Nếu trồng cà chua thì cần 20 công và thu được 300 nghìn đồng trên mỗi \({m^2}\). Nếu trồng cải bắp thì cần 30 công và thu được 400 nghìn đồng trên mỗi \({m^2}\). Hỏi cần cần trồng mỗi loại cây trên diện tích bao nhiêu để tthu được nhiều tiền nhất mà tổng số công không quá 180?Bài 19 :
Một xưởng nhỏ sản xuất hai loại sản phẩm A và B, mỗi cân sản phẩm loại A cần 2 cân nguyên liệu và 30 giờ sản xuất, mức lợi nhuận đem lại là 400 nghìn đồng/kg. Một cân sản phẩm loại B cần 4 cân nguyên liệu và 15 giờ sản xuất, mức lợi nhuận đem lại là 300 nghìn đồng. Mỗi ngày xưởng có 200 cân nguyên liệu và 1200 giờ làm việc. Vậy mỗi ngày xưởng đó nên sản xuất mỗi loại sản phẩm bao nhiêu kg để thu về mức lợi nhuận cao nhất?
Bài 20 :
Công ty X trong đợt hỗ trợ người dân cần thuê xe để chở ít nhất 120 người và 6,5 tấn hàng. Nơi thuê có 2 loại xe là A và B, loại xe A có 8 chiếc và xe B có 9 chiếc. Một chiếc xe loại A cho thuê với giá 3 triệu đồng, loại xe B thuê với giá 4 triệu đồng. Biết rằng mỗi chiếc xe loại A có thể chở tối đa 10 người và 2 tấn hàng. Mỗi chiếc xe loại B có thể chở tối đa 20 người và 0,5 tấn hàng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí là thấp nhất?Bài 21 :
Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24g hương liệu, 9 lít nước và 210g đường để pha chế nước cam và nước táo.
Để pha chế 1 lít nước cam cần 30g đường, 1 lít nước và 1g hương liệu.
Để pha chế 1 lít nước táo cần 10g đường, 1 lít nước và 4g hương liệu.
Gọi x, y lần lượt là số lít nước cam, nước táo được tạo thành.
a) Biểu thức biểu diễn số gam đường cần dùng là 30x + 10y.
b) Biểu thức biểu diễn số gam hương liệu cần dùng là x + y.
c) Cặp (x; y) thỏa mãn bài toán thuộc miền nghiệm của hệ \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{3x + y \le 21}\\{x + y \le 9}\\{x + 4y \le 24}\end{array}} \right.\).
d) Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Để điểm thưởng lớn nhất thì cần pha chế 4 lít nước cam và 5 lít nước táo.
Bài 22 :
Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 100 kg chất A và 9 kg chất B. Từ mỗi tấn nguyên liệu loại I giá 5 triệu đồng, có thể chiết xuất được 20 kg chất A. Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng có thể chiết xuất được 1,5 kg chất B. Biết mỗi kg chất A có giá 0,5 triệu đồng, mỗi kg chất B có giá 5 triệu đồng. Hỏi phải dùng bao nhiêu tấn nguyên liệu loại I để lợi nhuận thu về là lớn nhất, biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 8 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II.
Bài 23 :
Trong một cuộc thi gói bánh vào dịp năm mới, mỗi đội chơi được sử dụng tối đa 20 kg gạo nếp, 2 kg thịt ba chỉ, 5 kg đậu xanh để gói bánh chưng và bánh tét. Để gói một cái bánh chưng cần 0,4 kg gạo nếp, 0,05 kg thịt và 0,1 kg đậu xanh. Để gói một cái bánh tét cần 0,6 kg gạo nếp, 0,075 kg thịt và 0,15 kg đậu xanh. Gọi số bánh chưng gói được là x, số bánh tét gói được là y.
a) Biểu thức biểu diễn số kg gạo nếp cần dùng là 0,4x + 0,6y.
b) Biểu thức biểu diễn số thịt ba chỉ cần dùng là 0,05x + 0,1y.
c) Cặp (x; y) thỏa mãn bài toán thuộc miền nghiệm của hệ \(\left\{ {\begin{array}{*{20}{c}}{2x + 3y \le 80}\\{x,y \ge 0}\end{array}} \right.\).
d) Mỗi cái bánh chưng nhận được 5 điểm thưởng, mỗi cái bánh tét nhận được 7 điểm thưởng. Để điểm thưởng lớn nhất thì gói 35 cái bánh chưng và 5 cái bánh tét.
Bài 24 :
Một phân xưởng có hai máy đặc chủng \({M_1}\), \({M_2}\) sản xuất hai loại sản phẩm kí hiệu là A và B. Một tấn sản phẩm loại A lãi 2 triệu đồng, một tấn sản phẩm loại B lãi 1,6 triệu đồng. Muốn sản xuất một tấn sản phẩm loại A phải dùng máy \({M_1}\) trong 3 giờ và máy \({M_2}\) trong 1 giờ. Muốn sản xuất một tấn sản phẩm loại B phải dùng máy
\({M_1}\) trong 1 giờ và máy \({M_2}\) trong 1 giờ. Một máy không thể dùng để sản xuất đồng thời hai loại sản phẩm. Máy \({M_1}\) làm việc không quá 6 giờ một ngày, máy \({M_2}\) làm việc không quá 4 giờ một ngày. Hỏi số tiền lãi lớn nhất mà phân xưởng này có thể thu được trong một ngày là bao nhiêu (đơn vị: triệu đồng)?
Bài 25 :
Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140 kg chất A và 9 kg chất B. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20 kg chất A và 0,6 kg chất B. Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng có thể chiết xuất được 10 kg chất A và 1,5 kg chất B. Cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II. Gọi x, y lần lượt là số tấn nguyên liệu loại I và loại II cần dùng.
a) Biểu thức biểu diễn số kg chất A chiết xuất được là 20x + 10y.
b) Biểu thức biểu diễn số kg chất B chiết xuất được là 1,5x + 0,6y.
c) Cặp (x; y) thỏa mãn bài toán thuộc miền nghiệm của hệ \(\left\{ {\begin{array}{*{20}{c}}{2x + y \ge 14}\\\begin{array}{l}5x + 2y \ge 30\\0 \le x \le 9\\0 \le y \le 10\end{array}\end{array}} \right.\).
d) Phải dùng 5 tấn nguyên liệu loại I và 4 tấn nguyên liệu loại II để chi phí nguyên liệu là rẻ nhất.
Bài 26 :
Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit thức ăn mỗi ngày. Mỗi kg thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kg thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua tối đa 1,6 kg thịt bò và 1,1 kg thịt lợn; giá tiền 1 kg thịt bò là 45 nghìn đồng, 1 kg thịt lợn là 35 nghìn đồng. Hỏi gia đình đó phải bỏ ra ít nhất bao nhiêu tiền (đơn vị: nghìn đồng) để đạt các yêu cầu trên?
Bài 27 :
Trong một cuộc thi pha chế, mỗi đợi chơi được sử dụng tối đa 12g hương liệu, 9 lít nước và 315g đường để pha chế hai loại nước A và B. Để pha chết 1 lít nước A cần 45g đường, 1 lít nước và 0,5g hương liệu; để pha chế 1 lít nước B cần 15g đường, 1 lít nước và 2g hương liệu. Mỗi lít nước A nhận được 60 điểm thưởng, mỗi lít nước B nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước mỗi loại để đội chơi được số điểm thưởng là lớn nhất?
Bài 28 :
Một hợp tác xã chăn nuôi dự định trộn hai loại thức ăn gia súc \(X\) và gia súc \(Y\) để tạo thành thức ăn hỗn hợp cho gia súc. Giá một bao loại \(X\) là 250 nghìn đồng, giá một bao loại \(Y\) là 200 nghìn đồng. Mỗi bao loại \(X\) chứa 2 đơn vị chất dinh dưỡng A, 2 đơn vị chất dinh dưỡng B và 2 đơn vị chất dinh dưỡng C. Mỗi bao loại \(Y\) chứa 1 đơn vị chất dinh dưỡng A, 9 đơn vị chất dinh dưỡng B và 3 đơn vị chất dinh dưỡng C. Tìm chi phí nhỏ nhất để mua hai loại thức ăn gia súc \(X\) và \(Y\) sao cho hỗn hợp thu được tối thiểu 12 đơn vị chất dinh dưỡng A, 36 đơn vị chất dinh dưỡng B và 24 đơn vị chất dinh dưỡng C.
A. \(1,95\) triệu đồng.
B. \(4,5\) triệu đồng.
C. \(1,85\) triệu đồng.
D. \(1,7\) triệu đồng.
Bài 29 :
Giả sử một người ăn kiêng cần được cung cấp ít nhất 300 calo, 36 đơn vị vitamin A và 90 đơn vị vitamin C mỗi ngày từ hai loại đồ uống / và //. Mỗi cốc đồ uống / cung cấp 60 calo, 12 đơn vị vitamin A và 10 đơn vị vitamin C.
Mỗi cốc đồ uống // cung cấp 60 calo, 6 đơn vị vitamin A và 30 đơn vị vitamin C. Biết rằng một cốc đồ uống / có giá 12 nghìn đồng và một cốc đồ uống // có giá 15 nghìn đồng.
a) Gọi x và y tương ứng là số cốc đồ uống / và //. Viết các phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình và xác định miền nghiệm của hệ đó.
b) Gọi F (nghìn đồng) là số tiền phải trả cho x cốc đồ uống / và y là số tiền phải trả cho y cốc đồ uống //. Hãy biểu diễn F theo x và y.
c) Biết rằng F đạt giá trị nhỏ nhất trên miền nghiệm tìm được ở câu a tại một trong các đỉnh của miền nghiệm, tìm giá trị nhỏ nhất đó. Từ đó suy ra người đó cần uống bao nhiêu cốc loại / và loại // để chi phí là nhỏ nhất. mà vẫn đáp ứng được yêu cầu hằng ngày.
Bài 30 :
Anh Trung có kế hoạch đầu tư 400 triệu đồng vào hai khoản X và Y. Để đạt được lợi nhuận thì khoản X phải đầu tư ít nhất 100 triệu đồng và số tiền đầu tư cho khoản Y không nhỏ hơn số tiền cho khoản X. Viết hệ bất phương trình bậc nhất hai ẩn để mô tả hai khoản đầu tư đó và biểu diễn miền nghiệm của hệ bất phương trình vừa tìm được.












