Cho hai vectơ $\overrightarrow a$ và $\overrightarrow b$ thỏa mãn $\left| {\overrightarrow a } \right| = 6,\,\,\left| {\overrightarrow b } \right| = 8$ và $\left| {\overrightarrow a  + \overrightarrow b } \right| = 10.$

a) Tính tích vô hướng $\overrightarrow a .\left( {\overrightarrow a  + \overrightarrow b } \right).$

b) Tính số đo của góc giữa hai vectơ $\overrightarrow a$ và $\overrightarrow a  + \overrightarrow b .$

Bài 1 :

Tích vô hướng và góc giữa hai vectơ $\overrightarrow u  = \left( {0; - 5} \right),\;\overrightarrow v  = \left( {\sqrt 3 ;1} \right)$

Bài 2 :

Trong mặt phẳng tọa độ Oxy, cho hai vectơ không cùng phương $\overrightarrow u  = \left( {x;y} \right)$ và $\overrightarrow v  = \left( {x';y'} \right)$.

a) Xác định tọa độ của các điểm A và B sao cho $\overrightarrow {OA}  = \overrightarrow u ,\;\overrightarrow {OB}  = \overrightarrow v .$

b) Tính $A{B^2},O{A^2},O{B^2}$ theo tọa độ của A và B.

c) Tính $\overrightarrow {OA} .\overrightarrow {OB}$ theo tọa độ của A, B.

Bài 3 :

Cho hai vectơ cùng phương $\overrightarrow u  = \left( {x;y} \right)$ và $\overrightarrow v  = \left( {kx;ky} \right)$. Hãy kiểm tra công thức $\overrightarrow u .\overrightarrow v  = k\left( {{x^2} + {y^2}} \right)$ theo từng trường hợp sau:

a) $\overrightarrow u  = \overrightarrow 0$

b) $\overrightarrow u  \ne \overrightarrow 0$ và $k \ge 0$

c) $\overrightarrow u  \ne \overrightarrow 0$ và $k < 0$

Bài 4 :

Cho tam giác ABC. Giá trị của biểu thức $\overrightarrow {BA} .\overrightarrow {CA}$ bằng:

A. AB. AC. cos$\widehat {BAC}$   

B. – AB. AC. cos$\widehat {BAC}$            

C. AB. AC. cos$\widehat {ABC}$   

D. AB. AC. cos$\widehat {ACB}$

Bài 5 :

Cho tam giác ABC. Giá trị của biểu thức $\overrightarrow {AB} .\overrightarrow {BC}$ bằng:

A. AB. BC. cos$\widehat {ABC}$   

B. AB. AC. cos$\widehat {ABC}$               

C. – AB. BC. cos$\widehat {ABC}$

D. AB. BC. cos$\widehat {BAC}$

Bài 6 :

Cho đoạn thẳng AB. Tập hợp các điểm M nằm trong mặt phẳng thoả mãn $\overrightarrow {MA} .\overrightarrow {MB}  = 0$ là:

A. Đường tròn tâm A bán kính AB                

B. Đường tròn tâm B bán kính AB                

C. Đường trung trực của đoạn thẳng AB       

D. Đường tròn đường kính AB

Bài 7 :

Nếu hai điểm M, N thoả mãn $\overrightarrow {MN} .\overrightarrow {NM}  =  - 9$ thì:

A. MN = 9                  

B. MN = 3                  

C. MN = 81                

D. MN = 6

Bài 8 :

Cho hình thoi ABCD cạnh a và $\widehat A$= 120°. Tính $\overrightarrow {AC} .\overrightarrow {BC}$.

Bài 9 :

Cho các vectơ $\overrightarrow a ,\overrightarrow b  \ne \overrightarrow 0$. Phát biểu nào sau đây là đúng?

A. $\overrightarrow a .\overrightarrow b  = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\left| {\cos \left( {\overrightarrow a ,\overrightarrow b } \right)} \right|$

B. $\left| {\overrightarrow a .\overrightarrow b } \right| = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)$

C. $\overrightarrow a .\overrightarrow b  = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\sin \left( {\overrightarrow a ,\overrightarrow b } \right)$

D. $\overrightarrow a .\overrightarrow b  = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)$

Bài 10 :

Trong mặt phẳng Oxy, cho hai đường thẳng $\Delta$ đi qua điểm ${M_0}\left( {{x_0};{y_0}} \right)$ và vectơ $\overrightarrow n  = \left( {a;b} \right)$ và $\overrightarrow u  = \left( {b; - a} \right)$ khác vectơ 0. Cho biết $\overrightarrow u$ có giá song song hoặc trùng với $\Delta$.

a) Tính tích vô hướng $\overrightarrow n \overrightarrow {.u}$ và nêu nhận xét về phương của hai vectơ $\overrightarrow n ,\overrightarrow u$

b) Gọi $M\left( {x;y} \right)$ là điểm di động trên $\Delta$. Chứng tỏ rằng vectơ $\overrightarrow {{M_0}M}$ luôn cùng phương với vectơ $\overrightarrow u$ và luôn vuông góc với vectơ $\overrightarrow n$

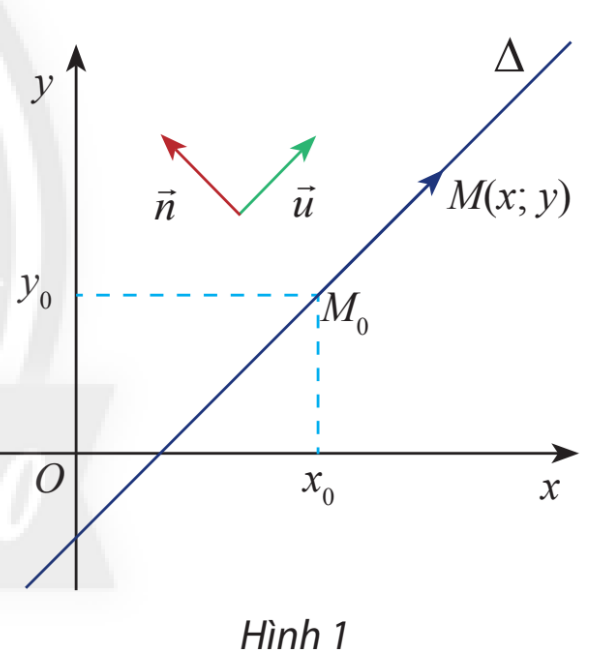
Bài 11 :

Trong mặt phẳng toạ độ Oxy, cho $\overrightarrow i$và $\overrightarrow j$  là vectơ đơn vị trên trục hoành Ox và ở trên trục tung Oy.

a) Tính ${\overrightarrow i ^2};{\overrightarrow j ^2};\overrightarrow i .\overrightarrow j$.

b) Cho $\overrightarrow u  = \left( {{x_1},{y_1}} \right)$, $\overrightarrow v  = \left( {{x_2},{y_2}} \right)$. Tính tích vô hướng $\overrightarrow u .\overrightarrow v$.

Bài 12 :

Trong mặt phẳng Oxy cho tam giác ABC, biết A(0;5), B(-2;8) và C(6;9). Giả sử điểm H(a;b) là chân đường cao vẽ từ đỉnh A của tam giác ABC. Tính $b + \frac{1}{2}a$?