Cho $P = \frac{1}{{x - 1}} + \frac{x}{{{x^2} + x + 1}} + \frac{{2x + 1}}{{1 - {x^3}}}$ với $x \ne 1.$

a) Rút gọn biểu thức $P.$

b) Tính giá trị của biểu thức $P$ tại $x = 2.$

c) Chứng minh $P > 0$ với $x > 0,\,x \ne 1.$

Bài 1 :

Cho biểu thức $A = \left( {\frac{1}{{x - 2}} - \frac{{2x}}{{4 - {x^2}}} + \frac{1}{{2 + x}}} \right).\left( {\frac{2}{x} - 1} \right)$

a) Rút gọn A.

b) Tính giá trị của biểu thức A tại x thỏa mãn: ${x^2} + 3x = 0$.

c) Tìm x để $A = \frac{1}{2}$.

d) Tìm x nguyên để A nguyên dương.

Bài 2 :

Cho các biểu thức $P = \frac{1}{{x + 5}} + \frac{2}{{x - 5}} - \frac{{2x + 10}}{{\left( {x + 5} \right)\left( {x - 5} \right)}}$; $Q = \frac{{x - 4}}{{{x^2} - 25}}$ với $x \ne  \pm 5$.

a) Tính giá trị Q với $x = 6$.

b) Rút gọn biểu thức P.

c) Đặt $A = \frac{P}{Q}$. Tìm các giá trị nguyên của x để A nhận giá trị nguyên.

Bài 3 :

Thực hiện các phép tính sau:

a) $\dfrac{{{x^2} - 9}}{{x - 2}}:\dfrac{{x - 3}}{x}$                       

b) $\dfrac{x}{{{z^2}}} \cdot \dfrac{{xz}}{{{y^3}}}:\dfrac{{{x^3}}}{{yz}}$                   

c) $\dfrac{2}{x} - \dfrac{2}{x}:\dfrac{1}{x} + \dfrac{4}{x} \cdot \dfrac{{{x^2}}}{2}$   

Bài 4 :

Tính:

a) $\left( {\dfrac{{1 - x}}{x} + {x^2} - 1} \right):\dfrac{{x - 1}}{x}$       

b) $\left( {\dfrac{1}{{{x^2}}} - \dfrac{1}{x}} \right) \cdot \dfrac{{{x^2}}}{y} + \dfrac{x}{y}$                

c) $\dfrac{3}{x} - \dfrac{2}{x}:\dfrac{1}{x} + \dfrac{1}{x} \cdot \dfrac{{{x^2}}}{3}$

Bài 5 :

Trên một dòng sông, một con thuyền đi xuôi dòng với tốc độ $x + 3$ km/h và đi ngược dòng với tốc độ $x - 3$ km/h ($x > 3)$.

a) Xuất phát từ bến A, thuyền đi xuôi dòng trong 4 giờ, rồi đi ngược dòng trong 2 giờ. Tính quãng đường thuyền đã đi. Lúc này thuyền cách bến A bao xa?

b) Xuất phát từ bến A, thuyền đi xuôi dòng đến bến B cách bến A $15$km, nghỉ $30$ phút, rồi quay về bến A. Sau bao lâu kể từ lúc xuất phát thì thuyền quay về đến bến A?

Bài 6 :

Thực hiện phép tính:

$a)\dfrac{x}{{xy + {y^2}}} - \dfrac{y}{{{x^2} + xy}}$                            

$b)\dfrac{{{x^2} + 4}}{{{x^2} - 4}} - \dfrac{x}{{x + 2}} - \dfrac{x}{{2 - x}}$

$c)\dfrac{{{a^2} + ab}}{{b - a}}:\dfrac{{a + b}}{{2{{\rm{a}}^2} - 2{b^2}}}$                          

$d)\left( {\dfrac{{2{\rm{x}} + 1}}{{2{\rm{x}} - 1}} - \dfrac{{2{\rm{x}} - 1}}{{2{\rm{x}} + 1}}} \right):\dfrac{{4{\rm{x}}}}{{10{\rm{x}} - 5}}$

Bài 7 :

Cho biểu thức:

$A = \left( {\dfrac{{x + 1}}{{2{\rm{x}} - 2}} + \dfrac{3}{{{x^2} - 1}} - \dfrac{{x + 3}}{{2{\rm{x}} + 2}}} \right).\dfrac{{4{{\rm{x}}^2} - 4}}{5}$

a) Viết điều kiện xác định của biểu thức A

b) Chứng minh giá trị của biểu thức A không phụ thuộc vào giá trị của biến.

Bài 8 :

Cho biểu thức:

$B = \left( {\dfrac{{5{{x}} + 2}}{{{x^2} - 10{{x}}}} + \dfrac{{5{{x}} - 2}}{{{x^2} + 10{{x}}}}} \right).\dfrac{{{x^2} - 100}}{{{x^2} + 4}}$

a) Viết điều kiện xác định của biểu thức B

b) Rút gọn B và tính giá trị của biểu thức B tại x = 0,1

c) Tìm số nguyên x để biểu thức B nhận giá trị nguyên.

Bài 9 :

Số tiền hằng năm A (triệu đô la Mỹ) mà người Mỹ chi cho việc mua đồ ăn, đồ uống khi ra khỏi nhà và dân số P (triệu người) hằng năm của nước Mỹ từ năm 2000 đến năm 2006 lần lượt cho bởi công thức sau:

$A = \dfrac{{ - 8242,58t + 348299,6}}{{ - 0,06t + 1}}$ với $0 \le t \le 6;P = 2,71t + 282,7$ với $0 \le t \le 6$

Trong đó, t là số năm tính từ năm 2000, t = 0 tương ứng với năm 2000

(Nguồn: U.S Bureau of Economic Analysis and U.S Census Bureau)

Viết phân thức biểu thị (theo t) số tiền bình quân hằng năm mà mỗi người Mỹ đã chi cho việc mua đồ ăn, đồ uống khi ra khỏi nhà.

Bài 10 :

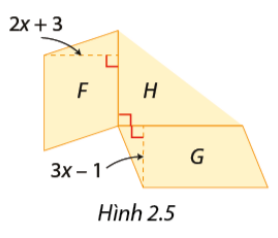
Trong Hình 2.5, hình bình hành F có diện tích là $8{x^2} + 14x + 3$ mét vuông và chiều cao là $2x + 3$ mét. Hình bình hành G có diện tích là $12{x^2} - 4x$ mét vuông và chiều cao là $3x - 1$ mét. Tính diện tích của tam giác vuông H theo x.

Bài 11 :

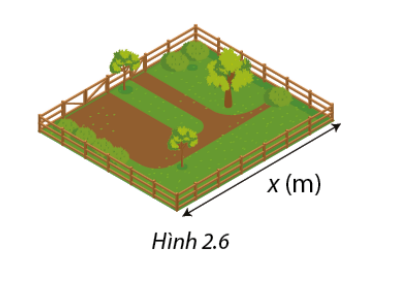
Một hàng rào được dựng bao quanh một mảnh đất hình chữ nhật diện tích $500{m^2}$. Gọi $x$ (m) là độ dài một cạnh của hàng rào.

a)     Viết một phân thức theo $x$ biểu diễn chu vi của hàng rào.

b)    Tính chu vi đó khi $x = 25\left( m \right)$.

Bài 12 :

Tính:

a) $\left( {a + 1 + \frac{{1 - 2{a^2}}}{{a - 1}}} \right):\left( {1 - \frac{1}{{1 - a}}} \right)$;

b) $\left( {\frac{a}{{{b^2}}} - \frac{1}{a}} \right):\left( {\frac{1}{b} + \frac{1}{a}} \right)$;

c) $\left( {a - \frac{{4ab}}{{a + b}} + b} \right).\left( {a + \frac{{4ab}}{{a - b}} - b} \right)$;

d) $ab + \frac{{ab}}{{a + b}}\left( {\frac{{a + b}}{{a - b}} - a - b} \right)$.

Bài 13 :

Rút gọn rồi tính giá trị của biểu thức:

a)     $A = \left( {\frac{{{x^2} + {y^2}}}{{{x^2} - {y^2}}} - 1} \right).\frac{{x - y}}{{2y}}$ tại $x = 5;y = 7$

b)    $B = \frac{{2x + y}}{{2{x^2} - xy}} + \frac{{8y}}{{{y^2} - 4{x^2}}} + \frac{{2x - y}}{{2{x^2} + xy}}$ tại $x =  - \frac{1}{2};y = \frac{3}{2}$

c)     $C = \left( {\frac{{{x^2}}}{y} - \frac{{{y^2}}}{x}} \right)\left( {\frac{{x + y}}{{{x^2} + xy + {y^2}}} + \frac{1}{{x - y}}} \right) - \frac{x}{y}$ tại $x =  - 15;y = 5$

Bài 14 :

Cho biểu thức: $D = \left( {\frac{{x + 2}}{{3x}} + \frac{2}{{x + 1}} - 3} \right):\frac{{2 - 4x}}{{x + 1}} - \frac{{3x - {x^2} + 1}}{{3x}}$

a)     Viết điều kiện xác định của biểu thức $D$

b)    Tính giá trị của biểu thức $D$ tại $x = 5947$

c)     Tìm giá trị của $x$ để $D$ nhận giá trị nguyên.

Bài 15 :

Cho biểu thức: $S = \frac{{{{\left( {x + 2} \right)}^2}}}{x}.\left( {1 - \frac{{{x^2}}}{{x + 2}}} \right) - \frac{{{x^2} + 6x + 4}}{x}$

a)     Rút gọn rồi tính giá trị của biểu thức $S$ tại $x = 0,1$

b)    Tìm giá trị lớn nhất của biểu thức $S$

Bài 16 :

Thực hiện phép tính:

$\begin{array}{l}a)\frac{{4{{\rm{x}}^2} - 1}}{{16{{\rm{x}}^2} - 1}}.\left( {\frac{1}{{2{\rm{x}} + 1}} + \frac{1}{{2{\rm{x}} - 1}} + \frac{1}{{1 - 4{{\rm{x}}^2}}}} \right)\\b)\left( {\frac{{x + y}}{{xy}} - \frac{2}{x}} \right).\frac{{{x^3}{y^3}}}{{{x^3} - {y^3}}}\end{array}$

Bài 17 :

Tìm đa thức P trong các đẳng thức sau:

a) $P + \frac{1}{{x + 2}} = \frac{x}{{{x^2} - 2{\rm{x}} + 4}}$

b) $P - \frac{{4\left( {x - 2} \right)}}{{x + 2}} = \frac{{16}}{{x - 2}}$

c) $P.\frac{{x - 2}}{{x + 3}} = \frac{{{x^2} - 4{\rm{x}} + 4}}{{{x^2} - 9}}$

d) $P:\frac{{{x^2} - 9}}{{2{\rm{x}} + 4}} = \frac{{{x^2} - 4}}{{{x^2} + 3{\rm{x}}}}$

Bài 18 :

Rút gọn biểu thức sau:

a) $\frac{2}{{3{\rm{x}}}} + \frac{x}{{x - 1}} + \frac{{6{{\rm{x}}^2} - 4}}{{2{\rm{x}}\left( {1 - x} \right)}}$

b) $\frac{{{x^3} + 1}}{{1 - {x^3}}} + \frac{x}{{x - 1}} - \frac{{x + 1}}{{{x^2} + x + 1}}$

c) $\left( {\frac{2}{{x + 2}} - \frac{2}{{1 - x}}} \right).\frac{{{x^2} - 4}}{{4{{\rm{x}}^2} - 1}}$

d) $1 + \frac{{{x^3} - x}}{{{x^2} + 1}}\left( {\frac{1}{{1 - x}} - \frac{1}{{1 - {x^2}}}} \right)$

Bài 19 :

Bài 20 :

Cho biểu thức $N = \left( {\frac{1}{{x + 1}} + \frac{x}{{x - 1}} + \frac{{{x^2}}}{{{x^2} - 1}}} \right).\frac{{x - 1}}{{2 + x}}$.

a) Viết điều kiện xác định của biểu thức $N$

b) Rút gọn biểu thức $N$

c) Tính giá trị của biểu thức $N$ khi $\left| x \right| = 2$

Bài 21 :

Cho $\frac{1}{x} + \frac{1}{y} + \frac{1}{z} = \frac{1}{{x + y + z}}$. Chứng minh rằng $\frac{1}{{{x^{2023}}}} + \frac{1}{{{y^{2023}}}} + \frac{1}{{{z^{2023}}}} = \frac{1}{{{x^{2023}} + {y^{2023}} + {z^{2023}}}}$

Bài 22 :

Cho $A = \frac{{x + 1}}{{x - 2}} + \frac{{x - 1}}{{x + 2}} + \frac{{{x^2} + 4x}}{{4 - {x^2}}}$ với $x \ne  \pm 2.$

a) Rút gọn biểu thức $A$.

b) Tính giá trị của $A$ khi $x = 4$.

c) Tìm giá trị nguyên của $x$ để $A$ nhận giá trị nguyên dương.

Bài 23 :

Cho biểu thức $A = \frac{{5x - 2}}{{{x^2} - 4}} - \frac{3}{{x + 2}} + \frac{x}{{x - 2}}$.

a) Tìm điều kiện xác định của biểu thức $A.$

b) Rút gọn biểu thức $A.$

c) Tính giá trị của biểu thức $A$ với $x$ thỏa mãn $\left| {x + 3} \right| = 5.$

Bài 24 :

Giải phương trình

a) $2\left( {x + 3} \right)\left( {x - 4} \right) = \left( {2x - 1} \right)\left( {x + 2} \right) - 27$

b) ${x^2} - 4 - \left( {x + 5} \right)\left( {2 - x} \right) = 0$

c) $\frac{{x + 2}}{{x - 2}} - \frac{{x - 2}}{{x + 2}} = \frac{4}{{{x^2} - 4}}$

d) $\frac{{x + 1}}{{x - 1}} - \frac{{x - 2}}{{x + 3}} + \frac{4}{{{x^2} + 2x - 3}} = 0$

Bài 25 :

Thực hiện các phép tính sau:

a) $\left( {\frac{1}{{{x^2} + x}} - \frac{{2 - x}}{{x + 1}}} \right):\left( {\frac{1}{x} + x - 2} \right)$;

b) $\left( {\frac{{3x}}{{1 - 3x}} + \frac{{2x}}{{3x + 1}}} \right):\frac{{6{x^2} + 10x}}{{1 - 6x + 9{x^2}}}$

Bài 26 :

Rút gọn các biểu thức sau:

a) $\left( {\frac{9}{{{x^3} - 9x}} + \frac{1}{{x + 3}}} \right):\left( {\frac{{x - 3}}{{{x^2} + 3x}} - \frac{x}{{3x + 9}}} \right)$;

b) $\frac{{x + 1}}{{x + 2}}\left( {\frac{{x + 2}}{{x + 3}}:\frac{{x + 3}}{{x + 1}}} \right)$.

Bài 27 :

Cho biểu thức $P = \left( {\frac{1}{{x - 1}} - \frac{x}{{1 - {x^3}}}.\frac{{{x^2} + x + 1}}{{x + 1}}} \right):\frac{{2x + 1}}{{{x^2} + 2x + 1}}$

a) Viết điều kiện xác định của P.

b) Rút gọn biểu thức P.

c) Tính giá trị của P khi $x = \frac{1}{2}$.

Bài 28 :

a) Rút gọn biểu thức $P = \frac{{{{\left( {x + 2} \right)}^2}}}{x}.\left( {1 - \frac{{{x^2}}}{{x + 2}}} \right) - \frac{{{x^2} + 6x + 4}}{x}$

b) Tìm giá trị lớn nhất của P. 

Bài 29 :

Một bể nước có hai vòi thoát. Biết rằng khi bể chứa đầy nước thì thời gian cần thiết để xả hết nước trong bể mà chỉ dùng vòi thứ nhất là x (giờ) và thời gian cần thiết để xả hết nước trong bể mà chỉ dùng vòi thứ hai là y (giờ).

a) Viết phân thức biểu thị thời gian cần thiết để xả hết nước trong bể (khi bể chứa đầy nước) nếu mở cả hai vòi.

b) Tính thời gian cần thiết để xả hết nước trong bể (khi bể chứa đầy nước) nếu mở cả hai vòi, biết rằng khi chỉ mở một vòi, vòi thứ nhất xả hết nước trong 2 giờ, vòi thứ hai xả hết nước trong 3 giờ.

Bài 30 :

Hãy thực hiện các phép tính đã chỉ ra.

a) $\frac{{4{{\rm{x}}^2} - 1}}{{16{{\rm{x}}^2} - 1}}.\left( {\frac{1}{{2{\rm{x}} + 1}} + \frac{1}{{2{\rm{x}} - 1}} + \frac{1}{{1 - 4{{\rm{x}}^2}}}} \right)$;

b) $\left( {\frac{{x + y}}{{xy}} - \frac{2}{x}} \right).\frac{{{x^3}{y^3}}}{{{x^3} - {y^3}}}$.