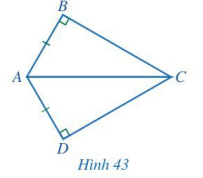
Cho Hình 43 có AB = AD, \(\widehat {ABC} = \widehat {ADC} = 90^\circ \). Chứng minh \(\widehat {ACB} = \widehat {ACD}\).

Bài 1 :

Cho tam giác ABC cân tại A. Từ A kẻ AH vuông góc với BC tại H, trên đoạn thẳng AH lấy điểm M tùy ý (M khác A và H). Chứng minh rằng:

a) BH = CH.

b) BA > BM.

Bài 2 :

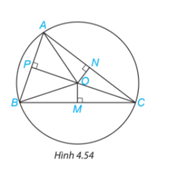
Cho ba điểm A, B, C nằm trên đường tròn tâm O và các điểm M, N, P như Hình 4.54. Hãy chỉ ra ba cặp tam giác vuông bằng nhau trong hình.

Bài 3 :

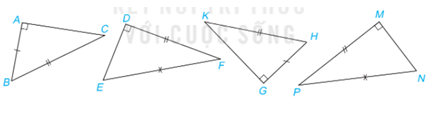
Hãy chỉ ra các cặp tam giác vuông bằng nhau dưới đây.

Bài 4 :

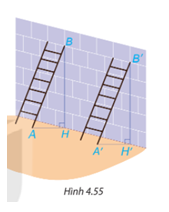
Có hai chiếc thang dài như nhau được dựa vào một bức tường với cùng độ cao BH = B’H’ như Hình 4.55. Các góc BAH và B'A'H có bằng nhau không? Vì sao?

Bài 5 :

Tương tự, vẽ thêm tam giác ABC có A = 90°, AB = 3 cm, BC = 5 cm.

a) Dùng thước thẳng có vạch chia hoặc compa kiểm tra xem AC có bằng A'C' không?

b) Hai tam giác ABC và A'B'C' có bằng nhau không?

Bài 6 :

Vẽ tam giác vuông ABC có A = 90°, AB = 3 cm, BC = 5 cm theo các bước sau:

• Dùng thước thẳng có vạch chia vẽ đoạn thẳng AB = 3 cm.

• Vẽ tia Ax vuông góc với AB và cung tròn tâm B bán kính 5 cm như Hình 4.51.

Cung tròn cắt tia Ax tại điểm C.

•Vẽ đoạn thẳng BC ta được tam giác ABC.

Bài 7 :

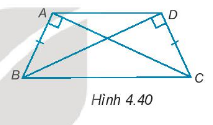
Cho 4 điểm A, B, C, D như hình 4.40 trong đó AB = DC. Chứng minh rằng:

a) AC = BD

b) \(AD\parallel BC\)

Bài 8 :

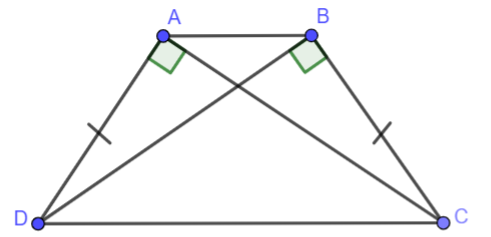
Cho hình vẽ bên. Biết \(\widehat {DAC} = \widehat {CBD} = {90^o},AD = BC\), hãy chứng minh rằng \(\widehat {BAD} = \widehat {ABC}\).

Bài 9 :

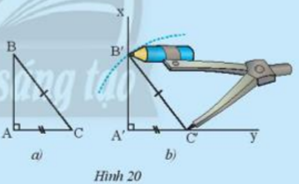
Cho tam giác ABC vuông tại A trong Hình 20a. Vẽ lên tờ giấy tam giác vuông A’B’C’có cạnh huyền và một cạnh góc vuông bằng với cạnh huyền và một cạnh góc vuông của tam giác ABC như sau:

- Vẽ góc vuông xA’ý, trên cạnh A’y vẽ đoạn A’C’= AC.

- Vẽ cung tròn tâm C’ bán kính bằng BC cắt A’x tại B’

Cắt rời tam giác A’B’C’. Em hãy cho biết có thể đặt chồng khít tam giác này lên tam giác kia không.

Bài 10 :

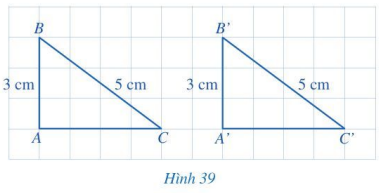
Cho hai tam giác vuông ABC và A’B’C’ có: \(\widehat A = \widehat {A'} = 90^\circ ,AB = A'B' = 3\)cm,\(BC = B'C' = 5\)cm (Hình 39). So sánh độ dài các cạnh AC và A’C’. 

Bài 11 :

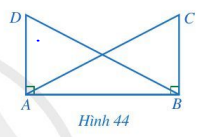
Cho Hình 44 có AC = BD, \(\widehat {ABC} = \widehat {BAD} = 90^\circ \). Chứng minh AD = BC.

Bài 12 :

Ở Hình 17 có ba điểm A, B, C thẳng hàng; AD và BE vuông góc với AB; AD = BC; DC = CE. Chứng minh:

a) ΔDAC = ΔCBE;

b) \(\widehat {DCE} = 90^\circ \).

Bài 13 :

a) Chứng minh \(\Delta AMB = \Delta DMC\).

b) Trên tia đối của tia \(CD\), lấy điểm \(I\) sao cho \(CI = CA\), qua điểm \(I\) vẽ đường thẳng song song với \(AC\) cắt \(AB\) tại \(E\). Chứng minh \(\Delta ACE = \Delta ICE\), từ đó suy ra \(\Delta ACE\) là tam giác vuông cân.

Bài 14 :

A. \(BA = PM\).

B. $BA = PN$.

C. $CA = MN$.

D. $\angle A = \angle N$.