Một bể nước dạng hình hộp chữ nhật có chiều dài $2m$ ; chiều rộng $1,2m$ và chiều cao $1,4m$. Hiện tại, lượng nước trong bể chiếm \(\dfrac{2}{5}\) thể tích của bể. Hỏi cần phải đổ thêm vào bể bao nhiêu lít nước để được đầy bể nước?

Bài 1 :

Người ta làm một cái hộp dạng hình hộp chữ nhật bằng bìa. Biết hộp đó có chiều dài \(5dm\), chiều rộng \(3dm\) và chiều cao \(3dm\). Hỏi có thể xếp được bao nhiêu hình lập phương \(1d{m^3}\) để đầy cái hộp đó?

Bài 2 :

Muốn tính thể tích hình hộp chữ nhật ta lấy chiều dài nhân với chiều rộng rồi cộng với chiều cao (cùng đơn vị đo). Đúng hay sai?

Bài 3 :

Một hình hộp chữ nhật có chiều dài là \(a\), chiều rộng là \(b\), chiều cao là \(c\). Công thức tính thể tích \(V\) của hình hộp chữ nhật đó là:

Bài 4 :

Tính thể tích hình hộp chữ nhật có chiều dài là \(17cm\), chiều rộng là \(9cm\), chiều cao là \(11cm\).

Bài 5 :

Điền số thích hợp vào ô trống:

Bài 6 :

Điền số thích hợp vào ô trống:

Bài 7 :

Một bể nước hình hộp chữ nhật có các kích thước trong lòng bể là chiều dài $3m$ ; chiều rộng kém chiều dài \(1,8m\); chiều cao $1,5m$. Hỏi bể đó chứa được nhiều nhất bao nhiêu lít nước? (\(1\) lít \( = 1d{m^3}\))

Bài 8 :

Một bể cá cảnh hình hộp chữ nhật có chiều dài $1,8m$; chiều rộng $0,6m$ và chiều cao \(0,9m\) . Hỏi người ta phải đổ vào trong bể cá cảnh đó bao nhiêu lít nước để lượng nước trong bể cao $0,6m$?

Bài 9 :

Điền số thích hợp vào ô trống:

Bài 10 :

Một bể nước dạng hình hộp chữ nhật có thể tích là $30d{m^3}$, chiều cao là $0,4m$ . Biết đáy bể có chiều rộng là $1,5dm$. Tính chiều dài của đáy bể.

Bài 11 :

Điền số thích hợp vào ô trống (dạng thu gọn nhất có thể):

Bài 12 :

Điền số thích hợp vào ô trống:

Bài 13 :

Một bể cá dạng hình hộp chữ nhật có chiều dài \(90cm\), chiều rộng \(50cm\) và chiều cao \(75cm\). Mực nước ban đầu trong bể cao \(45cm\). Người ta cho vào bể một hòn đá có thể tích \(18d{m^3}\). Hỏi mực nước trong bể lúc này cao bao nhiêu xăng-ti-mét?

Bài 14 :

Một cái bể hình hộp chữ nhật có chiều dài là $1,5m$ , chiều rộng là $1,2m$ và chiều cao $0,9m$ . Bể đã hết nước. Người ta đổ vào đó 30 gánh nước, mỗi gánh 45 lít. Hỏi mặt nước còn cách miệng bể bao nhiêu xăng-ti-mét?

Bài 15 :

Điền số thích hợp vào ô trống:

Bài 16 :

Một cái bể hình hộp chữ nhật có chiều dài là $2,5m$; chiều rộng kém chiều dài $1,3m$; chiều cao gấp $1,5$ lần chiều rộng. Hiện tại, lượng nước trong bể chiếm \(45\% \) thể tích của bể. Hỏi cần phải cho thêm vào bể bao nhiêu lít nước để được đầy bể nước?

Bài 17 :

Một bể nước dạng hình hộp chữ nhật có các kích thước đo ở trong lòng bể là: chiều dài là $1,5m$; chiều rộng $1,2m$, chiều cao \(2m\). Mặt nước cách miệng bể \(0,5m\). Người ta mở khóa cho nước chảy ra khỏi bể, sau \(5\) giờ thì bể cạn. Hỏi nước chảy ra khỏi bể mỗi phút được bao nhiêu lít?

Bài 18 :

Điền số thích hợp vào các ô trống:

Bài 19 :

Đáy của một hình hộp chữ nhật có chiều dài \(6dm\), chiều rộng \(45cm\). Tính chiều cao của hình hộp chữ nhật đó, biết diện tích xung quanh của hình hộp đó là \(378d{m^2}\).

Bài 20 :

Điền số thích hợp vào ô trống:

Bài 21 :

Tính thể tích hình hộp chữ nhật có chiều dài 8 cm, chiều rộng 5 cm và chiều cao 6 cm.

Bài 22 :

Bố của Mai vừa làm một bể cá dạng hình chữ nhật với kích thước như hình dưới đây.

Tính thể tích của bể cá đó.

Bài 23 :

Số?

Việt tạo một khối hình bằng cách ghép 6 hình hộp chữ nhật như hình dưới đây. Biết mỗi hình hộp chữ nhật có chiều dài 10 cm, chiều rộng 5 cm và chiều cao 2 cm.

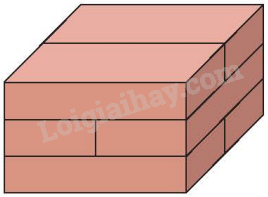
Thể tích khối hình đó là ? cm³

Bài 24 :

Chọn câu trả lời đúng.

Nam muốn xếp các khối gỗ dạng hình hộp chữ nhật có chiều dài 4 cm, chiều rộng 1 cm và chiều cao 1 cm vào một chiếc hộp. Chiếc hộp đó có dạng hình hộp chữ nhật với chiều dài 8 cm, chiều rộng 4 cm và chiều cao 4 cm.

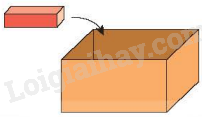
Hỏi Nam có thể xếp được nhiều nhất bao nhiêu khối gỗ như vậy vào hộp?

A. 8 khối

B. 16 khối

C. 32 khối

D. 64 khối

Bài 25 :

Tính thể tích của khối gỗ có hình dạng và kích thước như hình dưới đây.

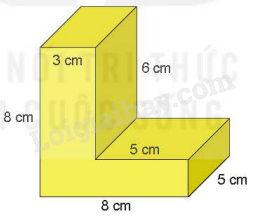
Bài 26 :

Quan sát hình vẽ và tính thể tích của tảng đá nằm trong bể nước.

Bài 27 :

Một bể cá có kích thước như hình dưới đây.

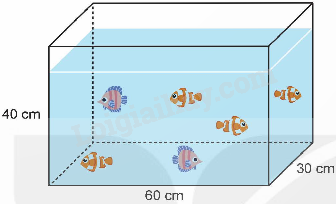
a) Tính thể tích bể cá.

b) Lúc đầu, mực nước trong bể bằng $\frac{3}{4}$chiều cao của bể. Sau đó Nam cho vào bể một viên đá cảnh thì mực nước lúc này cao 32,5 cm. Hỏi thể tích của viên đá cảnh đó là bao nhiêu xăng-ti-mét khối?

Bài 28 :

Một bể cá dạng hình hộp chữ nhật có chu vi đáy là 320 m, chiều rộng của đáy bằng $\frac{3}{5}$ chiều dài của đáy, chiều cao bể cá là 50 cm.

a) Tính chiều dài và chiều rộng đáy bể cá.

b) Biết mực nước ở bể cá là 40 cm. Hỏi lượng nước hiện có trong bể chiếm bao nhiêu phần trăm so với lượng nước khi đầy bể?

Bài 29 :

Quan sát hình vẽ:

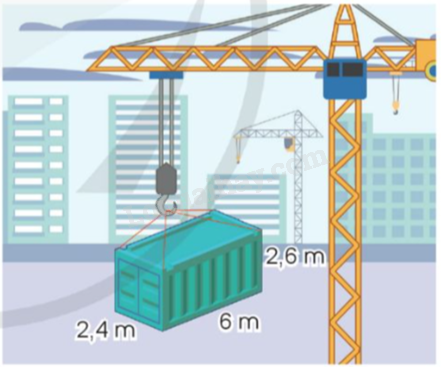
a) Tính thể tích thùng hàng.

b) Tính diện tích toàn phần của thùng hàng.

Bài 30 :

Ước lượng rồi lựa chọn số đo thể tích phù hợp: