Nội dung từ Loigiaihay.Com
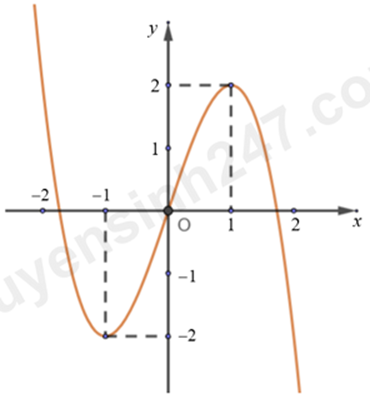
Cho hàm số bậc ba \(f\left( x \right)\) có đồ thị như hình vẽ. Số nghiệm thực của phương trình \({f^2}\left( x \right) - 3f\left( x \right) = - 2\) là:
-
A.
3
-
B.
4
-
C.
5
-
D.
6
Sử dụng tương giao đồ thị.
Ta có: \({f^2}\left( x \right) - 3f\left( x \right) = - 2 \Leftrightarrow {f^2}\left( x \right) - 3f\left( x \right) + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = 1\\f\left( x \right) = 2\end{array} \right..\)
Nhìn hình vẽ ta thấy:
Đồ thị hàm số \(y = f\left( x \right)\) cắt đường thẳng \(y = 1\) tại 3 điểm \( \Rightarrow \) Phương trình \(f\left( x \right) = 1\) có 3 nghiệm.
Đồ thị hàm số \(y = f\left( x \right)\) cắt đường thẳng \(y = 2\) tại 2 điểm \( \Rightarrow \) Phương trình \(f\left( x \right) = 1\) có 2 nghiệm.
Vậy phương trình đã cho có tất cả 5 nghiệm.
Đáp án : C

Các bài tập cùng chuyên đề
Bài 1 :
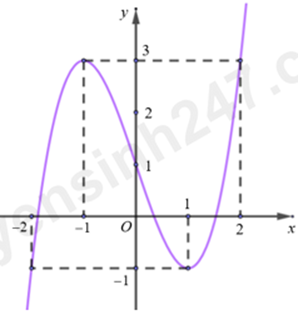
Cho hàm số bậc ba \(f(x)\) có đồ thị như hình vẽ. Hỏi có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left[ {f\left( x \right)} \right] = m\) có đúng \(4\) nghiệm phân biệt thuộc đoạn \(\left[ { - 1;2} \right]\)?
-
A.
1
-
B.
2
-
C.
3
-
D.
4
Bài 2 :
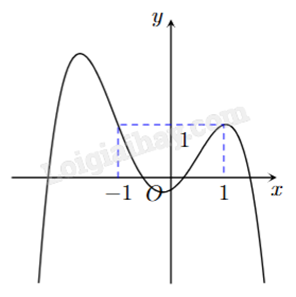
Cho hàm số đa thức bậc bốn y = f(x) có đồ thị như hình vẽ bên. Phương trình f(x) − 1 = 0 có bao nhiêu nghiệm thực phân biệt?
-
A.
3
-
B.
1
-
C.
2
-
D.
4
Bài 3 :
Trong mặt phẳng tọa độ Oxy cho đường thẳng (d): y = x + m – 1 và parabol (P): \(y = {x^2}\). Tìm m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có hoành độ lần lượt là \({x_1}\), \({x_2}\) thỏa mãn: \(4\left( {\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}}} \right) - {x_1}{x_2} + 3 = 0\).
Bài 4 :
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số \(y = 2{x^3} - 3{x^2} + 2\) cắt đồ thị hàm số \(y = {x^3} - 6{x^2} + 9x + m\) tại 3 điểm phân biệt?












