Nội dung từ Loigiaihay.Com
Viện Hàn Lâm Nhi khoa Mĩ (AAP) khuyến nghị, khối lượng cặp sách của học sinh tiểu học và trung học cơ sở không nên vượt quá 10% khối lượng cơ thể. Bạn Đức học lớp 7 có cân nặng 46 kg. Hằng ngày, bạn Đức đi học mang một chiếc cặp sách nặng 3,5 kg. Hôm nay, bạn Đức cần đem thêm một số quyển vở mới, mỗi quyển vở nặng \(\frac{4}{{25}}\) kg để tặng học sinh vùng lũ lụt. Bạn Đức có thể mang theo nhiều nhất bao nhiêu quyển vở để khối lượng cặp sách phù hợp với khuyến nghị trên?
Tính khối lượng cặp sách của bạn Đức khi biết cân nặng và tỉ số phần trăm khối lượng cặp sách so với cân nặng.
Từ đó tính khối lượng vở mới bạn Đức có thể mang nhiều nhất = khối lượng cặp sách – khối lượng chiếc cặp.
Tính số quyển vở tương ứng với \(\frac{4}{{25}}kg\).
Theo khuyến nghị, khối lượng cặp sách bạn Đức nên mang không vượt quá là:
46 . 10% = 4,6 (kg).
Khối lượng vở mới Đức có thể mang thêm nhiều nhất theo khuyến nghị là:
4,6 – 3,5 = 1,1 (kg).
1,1kg ứng với số quyển vở nặng \(\frac{4}{{25}}\)kg là: \(1,1:\frac{4}{{25}} = 1,1.\frac{{25}}{4} = 6,875\)
Do đó bạn Đức có thể mang theo nhiều nhất 6 quyển vở để khối lượng cặp sách phù hợp với khuyến nghị trên.

Các bài tập cùng chuyên đề
Bài 1 :
Tính:
\(\frac{5}{9}:\left( {\frac{1}{{11}} - \frac{5}{{22}}} \right) + \frac{7}{4}.\left( {\frac{1}{{14}} - \frac{2}{7}} \right)\)
-
A.
\(\frac{{ - 799}}{{216}}\)
-
B.
\(\frac{{ - 113}}{{35}}\)
-
C.
\( - 1\)
-
D.
\(\frac{{ - 961}}{{216}}\)
Bài 2 :
Tính: T = [ (-43,57) . 40 – 40. 26,43] : [ -72 . 63,6 – 4,9 . 64]
-
A.
0
-
B.
\(\frac{6}{7}\)
-
C.
\(\frac{{40}}{{49}}\)
-
D.
1
Bài 3 :
Em hãy nhắc lại thứ tự thực hiện phép tính đối với số tự nhiên rồi tính:
\(\begin{array}{l}a)10 + 36:2.3;\\b)[5 + 2.(9 - {2^3})]:7\end{array}\)
Bài 4 :
Tính giá trị của các biểu thức sau:
\(\begin{array}{l}a)\left( {\frac{2}{3} + \frac{1}{6}} \right):\frac{5}{4} + \left( {\frac{1}{4} + \frac{3}{8}} \right):\frac{5}{2}\\b)\frac{5}{9}:\left( {\frac{1}{{11}} - \frac{5}{{22}}} \right) + \frac{7}{4}.\left( {\frac{1}{{14}} - \frac{2}{7}} \right)\end{array}\)
Bài 5 :
Tính một cách hợp lí
\(\begin{array}{l}a) - 1,2 + ( - 0,8) + 0,25 + 5,75 - 2021\\b) - 0,1 + \frac{{16}}{9} + 11,1 + \frac{{ - 20}}{9}\end{array}\)
Bài 6 :
Để làm một cái bánh, cần \(2\frac{3}{4}\) cốc bột. Lan đã có \(1\frac{1}{2}\) cốc bột. Hỏi Lan cần thêm bao nhiêu cốc bột nữa?
Bài 7 :
Tính một cách hợp lí:
a) \(A = 32,125 - (6,325 + 12,125) - (37 + 13,675)\)
b) \(B = 4,75 + {\left( {\frac{{ - 1}}{2}} \right)^3} + 0,{5^2} - 3.\frac{{ - 3}}{8}\)
c) \(C = 2021,2345.2020,1234 + 2021,2345.( - 2020,1234)\)
Bài 8 :
Đặt một cặp dấu ngoặc “( )” để được biểu thức đúng.
2,2 – 3,3 + 4,4 – 5,5 = 0.
Bài 9 :
Tính:
a)\(1\frac{1}{2} + \frac{1}{5}.\left[ {\left( { - 2\frac{5}{6} + \frac{1}{3}} \right)} \right];\)
b)\(\frac{1}{3}.\left( {\frac{2}{5} - \frac{1}{2}} \right):{\left( {\frac{1}{6} - \frac{1}{5}} \right)^2}.\)
Bài 10 :
Tính nhanh:
a)\(\frac{{13}}{{23}}.\frac{7}{{11}} + \frac{{10}}{{23}}.\frac{7}{{11}};\)
b) \(\frac{5}{9}.\frac{{23}}{{11}} - \frac{1}{{11}}.\frac{5}{9} + \frac{5}{9}\)
c)\(\left[ {\left( { - \frac{4}{9}} \right) + \frac{3}{5}} \right]:\frac{{13}}{{17}} + \left( {\frac{2}{5} - \frac{5}{9}} \right):\frac{{13}}{{17}};\)
d) \(\frac{3}{{16}}:\left( {\frac{3}{{22}} - \frac{3}{{11}}} \right) + \frac{3}{{16}}:\left( {\frac{1}{{10}} - \frac{2}{5}} \right)\)
Bài 11 :
a) Tính diện tích hình thang ABCD có các kích thước như hình sau:
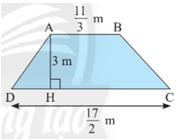
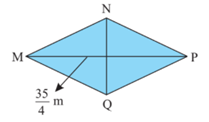
b) Hình thoi MNPQ có diện tích bằng diện tích hình thang ABCD ở câu a, đường chéo MP= \(\frac{{35}}{4}\)m. Tính độ dài NQ.
Bài 12 :
Tìm số hữu tỉ a, biết rằng lấy a nhân với \(\frac{1}{2}\) rồi cộng với \(\frac{3}{4}\), sau đó chia kết quả cho \(\frac{{ - 1}}{4}\) thì được số \( - 3\frac{3}{4}\).
Bài 13 :
Tính giá trị của mỗi biểu thức sau:
a) \(0,2 + 2,5:\frac{7}{2}\)
b) \(9.{\left( {\frac{{ - 1}}{3}} \right)^2} - {\left( { - 0,1} \right)^3}:\frac{2}{{15}}\)
Bài 14 :
Tính giá trị của mỗi biểu thức sau:
a) \(\left( {0,25 - \frac{5}{6}} \right).1,6 + \frac{{ - 1}}{3}\)
b) \(3 - 2.\left[ {0,5 + \left( {0,25 - \frac{1}{6}} \right)} \right]\)
Bài 15 :
Tính
a) \(\frac{1}{9} - 0,3.\frac{5}{9} + \frac{1}{3};\)
b) \({\left( {\frac{{ - 2}}{3}} \right)^2} + \frac{1}{6} - {\left( { - 0,5} \right)^3}.\)
Bài 16 :
Tính
a) \(\left( {\frac{4}{5} - 1} \right):\frac{3}{5} - \frac{2}{3}.0,5\)
b) \(1 - {\left( {\frac{5}{9} - \frac{2}{3}} \right)^2}:\frac{4}{{27}}\)
c)\(\left[ {\left( {\frac{3}{8} - \frac{5}{{12}}} \right).6 + \frac{1}{3}} \right].4\)
d) \(0,8:\left\{ {0,2 - 7.\left[ {\frac{1}{6} + \left( {\frac{5}{{21}} - \frac{5}{{14}}} \right)} \right]} \right\}\)
Bài 17 :
Một mảnh vườn có dạng hình chữ nhật với độ dài hai cạnh là 5,5 m và 3,75 m. Dọc theo các cạnh của mảnh vườn, người ta trồng các khóm hoa, cứ \(\frac{1}{4}\)m trồng một khóm hoa. Tính số khóm hoa cần trồng.
Bài 18 :
Cho miếng bìa có kích thước như hình vẽ bên (các số đo trên hình tính theo đơn vị đề-xi-mét).
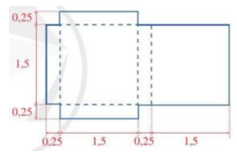
a) Tính diện tích của miếng bìa.
b) Từ miếng bìa đó, người ta gấp thành một hình hộp chữ nhật. Tính thể tích của hình hộp chữ nhật đó.
Bài 19 :
Tính:
a)\(0,3 - \frac{4}{9}:\frac{4}{3} \cdot \frac{6}{5} + 1\);
b)\({\left( {\frac{{ - 1}}{3}} \right)^2} - \frac{3}{8}:{(0,5)^3} - \frac{5}{2} \cdot ( - 4)\);
c)\(1 + 2:\left( {\frac{2}{3} - \frac{1}{6}} \right) \cdot ( - 2,25)\)
d)\(\left[ {\left( {\frac{1}{4} - 0,5} \right) \cdot 2 + \frac{8}{3}} \right]:2\).
Bài 20 :
Tính \(A = \left[ {\left( {\dfrac{1}{{81}} - \dfrac{3}{{162}}} \right).\dfrac{{81}}{{17}} + \dfrac{{35}}{{34}}} \right]:\left[ {\left( {\dfrac{9}{{51}} + \dfrac{7}{{102}}} \right).\dfrac{{102}}{5} + 2017} \right]\)
Bài 21 :
Tính
a)\(\left( { - 0,5} \right) - \left( { - 1 + \dfrac{2}{3}} \right):1,5 + \left( {\dfrac{{ - 1}}{4}} \right)\)
b)\(\left[ {\left( {\dfrac{{ - 7}}{8}} \right):\dfrac{{21}}{{16}}} \right] - \dfrac{5}{3}.\left( {\dfrac{1}{3} - \dfrac{7}{{10}}} \right)\)
c)\({\left[ {\left( {\dfrac{{ - 2}}{3}} \right) + \dfrac{3}{4}} \right]^2}.\dfrac{{12}}{5} - \dfrac{1}{5}\)
d)\({\left( {\dfrac{1}{{25}} - 0,4} \right)^2}:\dfrac{9}{{125}} - \left[ {\left( {1\dfrac{1}{3} - \dfrac{2}{5}} \right).\dfrac{3}{7}} \right]\)
e)\(\left\{ {3\dfrac{{17}}{{18}}.\left[ {\dfrac{5}{2} - \left( {\dfrac{1}{3} + \dfrac{2}{9}} \right)} \right]} \right\}:{\left[ {\left( {\dfrac{{ - 1}}{2}} \right) + 0,25} \right]^2}\)
Bài 22 :
Tính giá trị của mỗi biểu thức sau:
a) \(12.{\left( {\dfrac{2}{3} - \dfrac{5}{6}} \right)^2}\);
b) \(4.{\left( { - \dfrac{1}{2}} \right)^3} - 2.{\left( { - \dfrac{1}{2}} \right)^2} + 3.\left( { - \dfrac{1}{2}} \right) + 1\).
Bài 23 :
Tính giá trị của mỗi biểu thức sau:
a) \(\dfrac{{45}}{4} - \left( {2\dfrac{5}{7} + 5,25} \right)\);
b) \(\dfrac{5}{9}:2,4 - \dfrac{{41}}{9}:2,4\);
c) \(\left( { - \dfrac{3}{4} + \dfrac{5}{{13}}} \right).\dfrac{7}{2} - \left( {\dfrac{9}{4} - \dfrac{8}{{13}}} \right).\dfrac{7}{2}\).
Bài 24 :
Cho \(A = \dfrac{{13}}{{50}}.( - 15,5) - \dfrac{{13}}{{50}}.84\dfrac{1}{2};{\rm{ }}B = \dfrac{{{{( - 0,7)}^2}.{{( - 5)}^3}}}{{{{\left( { - \dfrac{7}{3}} \right)}^3}.{{\left( {\dfrac{3}{2}} \right)}^4}.{{( - 1)}^5}}}\).
Bạn An tính được giá trị của các biểu thức trên: \(A = - 26;{\rm{ }}B = \dfrac{{ - 20}}{{21}}\). Theo em, bạn An tính đúng hay sai?
Bài 25 :
Cho \(A = \dfrac{{\dfrac{{ - 1}}{2} - 5.{{\left( {\dfrac{3}{2}} \right)}^2}}}{{15\dfrac{2}{9} + {{\left( { - \dfrac{2}{3}} \right)}^2}}};{\rm{ }}B = \dfrac{7}{{12}}.3,4 - \dfrac{7}{{12}}.8,8\).
Tính \(A - 5B\).
Bài 26 :
Chọn dấu “<”, “>”, “=” thích hợp cho ?:
a) \(\dfrac{5}{6} - {\left( {\dfrac{1}{6}} \right)^2}\) ? \({\left( {\dfrac{5}{6} - \dfrac{1}{6}} \right)^2}\);
b) \(250.{\left( {\dfrac{1}{5} - \dfrac{1}{6}} \right)^2}\) ? \(250.{\left( {\dfrac{1}{5}} \right)^2} - \dfrac{1}{6}\);
c) \(3\dfrac{1}{5}:1,5 + 4\dfrac{2}{5}:1,5\) ? \(\left( {3\dfrac{1}{5} + 4\dfrac{2}{5}} \right):1,5\);
d) \(\left( {\dfrac{9}{{25}} - 2,18} \right):\left( {3\dfrac{4}{5} + 0,2} \right)\) ? \(\dfrac{9}{{25}}:3\dfrac{4}{5} - 2,18:0,2\).
Bài 27 :
Cho \(A = \left( {17,81:1,37 - \dfrac{{59}}{3}:\dfrac{{11}}{6}} \right) + \dfrac{{{{(0,8)}^3}}}{{{{(0,4)}^3}.11}}\).
Chứng minh rằng A + 1 là bình phương của một số tự nhiên.
Bài 28 :
Một vườn trường có dạng hình chữ nhật với độ dài hai cạnh là 26 m và 14 m. Người ta muốn rào xung quanh vườn, cứ cách 2 m đóng một cọc rào, mỗi góc vườn đều đóng một cọc rào và chỉ để một cửa ra vào vườn rộng 4 m. Tính số cọc rào cần dùng, biết rằng hai cạnh bên của cửa đồng thời cũng là hai cọc rào.
Bài 29 :
Quan sát biển báo giao thông ở Hình 7.
a) Tính diện tích của biển báo, biết rằng đường kính của biển báo là 87,5 cm (lấy \(\pi = 3,14\)).
b) Ở chính giữa của biển báo là hình chữ nhật được sơn màu trắng có chiều dài là 70,3 cm và chiều rộng là 12,3 cm. Phần còn lại của biển báo được sơn màu đỏ. Tính diện tích phần được sơn màu đỏ của biển báo.

Bài 30 :
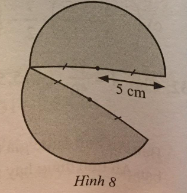
Người ta cắt một tấm tôn có dạng hình tròn bán kính 5 cm thành hai phần bằng nhau như Hình 8. Tính chu vi tấm tôn sau khi bị cắt (lấy \(\pi = 3,14\)).