Nội dung từ Loigiaihay.Com
Chứng tỏ rằng với mọi \(n \in \mathbb{N}\) thì \(2n + 1\) và \(3n + 1\) là hai số nguyên tố cùng nhau.
Hai số nguyên tố cùng nhau nếu ước chung lớn nhất của chúng bằng 1.
Giả sử ƯCLN(2n+1;3n+1) = d (d \( \in \mathbb{N}\)).
Chứng minh d = 1 nên \(2n + 1\) và \(3n + 1\) là hai số nguyên tố cùng nhau.
Gọi ƯCLN(2n+1;3n+1) = d (d \( \in \mathbb{N}\)).
Suy ra \(2n + 1 \vdots d\); \(3n + 1 \vdots d\).
Do đó \(3\left( {2n + 1} \right) \vdots d\); \(2\left( {3n + 1} \right) \vdots d\)
hay \(6n + 3 \vdots d\); \(6n + 2 \vdots d\)
Suy ra \(\left( {6n + 3} \right) - \left( {6n + 2} \right) \vdots d\) hay \(1 \vdots d\) suy ra d \( \in \) Ư(1) = {1; -1}
Mà \(d \in \mathbb{N}\) nên d = 1.
Do đó ƯCLN(2n+1;3n+1) = 1
Vậy \(2n + 1\) và \(3n + 1\) là hai số nguyên tố cùng nhau.

Các bài tập cùng chuyên đề
Bài 1 :
Số nguyên tố nhỏ hơn 30 là:
-
A.
23
-
B.
31
-
C.
27
-
D.
32
Bài 2 :
Hai số nguyên tố được gọi là sinh đôi nếu chúng hơn kém nhau hai đơn vị. Ví dụ 17 và 19 là hai số nguyên tố sinh đôi. Em hãy liệt kê các cặp số nguyên tố sinh đôi nhỏ hơn 40.
Bài 3 :
Tìm các ước và số ước của các số trong bảng bên.

Bài 4 :
Hãy chia các số cho trong bảng 2.1 thành hai nhóm: nhóm A gồm các số chỉ có hai ước, nhóm B gồm các số có nhiều hơn hai ước.
Bài 5 :
Suy nghĩ và trả lời câu hỏi:
a) Số 1 có bao nhiêu ước?
b) Số 0 có chia hết cho 2, 5, 7, 2017, 2018 không? Em có nhận xét gì về số ước của 0?
Bài 6 :
Lớp của bạn Hoàng có 37 học sinh. Trong một lần thi đồng diễn thể dục, các bạn lớp Hoàng muốn xếp thành các hàng có cùng số bạn để được một khối hình chữ nhật có ít nhất là hai hàng. Hỏi các bạn có thực hiện được không? Em hãy giải thích.
Bài 7 :
Hãy cho ví dụ về :
a) Hai số tự nhiên liên tiếp đều là số nguyên tố.
b) Ba số lẻ liên tiếp đều là số nguyên tố.
Bài 8 :
Mỗi khẳng định sau đúng hay sai?
a) Tích của hai số nguyên tố luôn là một số lẻ.
b) Tích của hai số nguyên tố có thể là một số chẵn.
c) Tích của hai số nguyên tố có thể là một số nguyên tố.
Bài 9 :
Lập bảng các số nguyên tố không vượt quá 100.
a) Hãy lập bảng các số nguyên tố không vượt quá 100 theo các hướng dẫn sau:
Lập bảng các số tự nhiên từ 1 đến 100 gồm 10 hàng, 10 cột như dưới đây.
- Gạch số 1.
- Giữ lại (đóng khung) số 2, gạch tất cả các số là bội của 2 mà lớn hơn 2.
- Giữ lại số 3, gạch tất cả các số là bội của 3 mà lớn hơn 3.
- Giữ lại số 5, gạch tất cả các số là bội của 5 mà lớn hơn 5.
- Giữ lại số 7, gạch tất cả các số là bội của 7 mà lớn hơn 7.
- Tiếp tục quá trình này cho đến khi tất cả các số được giữ lại hoặc bị gạch.
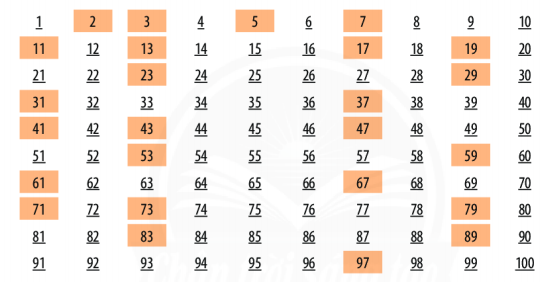
- Các số được giữ lại là tất cả các số nguyên tố bé hơn 100. Hãy liệt kê các số này.
b) Trả lời các câu hỏi sau:
Số nguyên tố nhỏ nhất là số nào?
Số nguyên tố lớn nhất trong phạm vi 100 là số nào?
Có phải mọi số nguyên tố đều là số lẻ không? Vì sao?
Có phải mọi số chẵn đều là hợp số không? Vì sao?
Bài 10 :
Dùng bảng các số nguyên tố ở cuối chương này (trang 48), em hãy tìm các số nguyên tố trong các số sau: 113; 143; 217; 529.
Bài 11 :
Hãy chỉ ra một số nguyên tố lớn hơn 40 và nhỏ hơn 50
Bài 12 :
a) Tìm các ước của mỗi số sau: 2,3,4,5,6,7,17,34.
b) Trong các số trên, những số nào có hai ước, những số nào có nhiều hơn hai ước?
Bài 13 :
Cho các số 11, 29, 35, 38. Trong các số đó:
a) Số nào là số nguyên tố? Vì sao?
b) Số nào là hợp số? Vì sao?
Bài 14 :
Tìm các ước nguyên tố của 23, 24, 26, 27.
Bài 15 :
Viết hai số chỉ có ước nguyên tố là 3.
Bài 16 :
Tìm một ước nguyên tố của 187.
Bài 17 :
a) Hãy nêu các số nguyên tố nhỏ hơn 30.
b) Tìm một ước nguyên tố của 91
Bài 18 :
Trong các số tự nhiên sau số nào là số nguyên tố?
-
A.
39
-
B.
27
-
C.
35
-
D.
2
Bài 19 :
Gọi P là tập hợp các số nguyên tố. Điền kí hiệu \( \in , \notin \)thích hợp vào chỗ chấm.
41 … P;
57 … P;
83 … P;
95 … P.
Bài 20 :
Dùng bảng nguyên tố tìm các số nguyên tố trong các số sau:
117;
131;
313;
469;
647
Bài 21 :
a) Viết mỗi số sau thành tổng của hai số nguyên tố:
16; 18; 20.
b) Viết 15 thành tổng của 3 số nguyên tố.
Bài 22 :
Tìm số nguyên tố p sao cho p +1 và p + 5 đều là số nguyên tố
Bài 23 :
a) Tìm số tự nhiên k để 3.k là số nguyên tố.
b) Tìm số tự nhiên k để 7.k là số nguyên tố.
Bài 24 :
-
A.
9 số
-
B.
10 số
-
C.
11 số
-
D.
12 số
Bài 25 :
Số 2 021 có thể viết thành tổng của hai số nguyên tố được không? Vì sao?
Bài 26 :
a) Năm 1742, nhà toán học người Đức Goldbach gửi cho nhà toán học Thụy Sĩ Euler một bức thư viết rằng: Mọi số tự nhiên lớn hơn 5 đều viết được thành tổng của ba số nguyên tố, ví dụ 7 = 2 + 2 + 3; 8 = 2 + 3 + 3.
Em hãy viết các số 17; 20 thành tổng của ba số nguyên tố.
b) Trong thư trả lời Goldbach, Euler nói rằng: Mọi số chẵn lớn hơn 2 đều viết được dưới dạng tổng của hai số nguyên tố.
Em hãy viết các số 36; 50 thành tổng của hai số nguyên tố.
Cả hai bài toán Goldbach và Euler nêu ra đến nay vẫn chưa có lời giải.
Bài 27 :
a) Tìm các ước nguyên tố của các số sau: 12, 36, 43.
b) Tìm các ước không phải là số nguyên tố của các số sau:21, 35, 47.
Bài 28 :
Hai bạn Ân, và Huệ tranh luận tính đúng, sai của các phát biểu sau:
a) Có ba số lẻ liên tiếp đều là số nguyên tố;
b) Có hai số nguyên tố mà tổng của chúng là số lẻ;
c) Mọi số nguyên tố đều là số lẻ;
d) Tổng của hai số nguyên tố bất kì là một số chẵn.
Bài 29 :
Ba số nguyên tố phân biệt có tổng là 106. Số lớn nhất trong ba số nguyên tố đó có thể lớn nhất bằng bao nhiêu?
Bài 30 :
Phân tích 225 và 1 200 ra thừa số nguyên tố rồi cho biết mỗi số đó chia hết cho những số nguyên tố nào












