Nội dung từ Loigiaihay.Com
Cho hàm số f(x) = x – sin2x.
a) \(f\left( 0 \right) = 0\); \(f\left( \pi \right) = \pi \).
b) Đạo hàm của hàm số đã cho là f’(x) = 1 + cos2x.
c) Nghiệm của phương trình f’(x) = 0 trên đoạn \(\left[ {0;\pi } \right]\) là \(\frac{\pi }{6}\) hoặc \(\frac{{5\pi }}{6}\).
d) Giá trị nhỏ nhất của f(x) trên đoạn \(\left[ {0;\pi } \right]\) là \(\frac{\pi }{6} - \frac{{\sqrt 3 }}{2}\).
a) \(f\left( 0 \right) = 0\); \(f\left( \pi \right) = \pi \).
b) Đạo hàm của hàm số đã cho là f’(x) = 1 + cos2x.
c) Nghiệm của phương trình f’(x) = 0 trên đoạn \(\left[ {0;\pi } \right]\) là \(\frac{\pi }{6}\) hoặc \(\frac{{5\pi }}{6}\).
d) Giá trị nhỏ nhất của f(x) trên đoạn \(\left[ {0;\pi } \right]\) là \(\frac{\pi }{6} - \frac{{\sqrt 3 }}{2}\).
a) Thay 0, \(\pi \) vào x rồi tính giá trị biểu thức.
b) Áp dụng công thức đạo hàm của hàm hợp lượng giác: (sinu)’ = u’.cosu.
c) Nếu \(\cos \alpha = m\) thì \(\cos x = m \Leftrightarrow \cos x = \cos \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = - \alpha + k2\pi \end{array} \right.\) \((k \in \mathbb{Z})\).
Dựa vào khoảng hoặc đoạn đề bài cho, tìm các giá trị k thỏa mãn rồi thay vào công thức nghiệm và kết luận.
d) Thay giá trị hai đầu mút của đoạn và các giá trị sao cho f’(x) = 0 vào f(x) và tìm giá trị nhỏ nhất.
a) Đúng. \(f\left( 0 \right) = 0 - \sin (2.0) = 0\) và \(f\left( \pi \right) = \pi - \sin (2\pi ) = \pi \).
b) Sai. f’(x) = 1 – 2cos2x.
c) Đúng. \(1 - 2\cos 2x = 0 \Leftrightarrow \cos 2x = \frac{1}{2} \Leftrightarrow \left[ \begin{array}{l}2x = \frac{\pi }{3} + k2\pi \\2x = - \frac{\pi }{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + k\pi \\x = - \frac{\pi }{6} + k\pi \end{array} \right.\) \((k \in \mathbb{Z})\).
+) \(0 \le x \le \pi \Leftrightarrow 0 \le \frac{\pi }{6} + k\pi \le \pi \Leftrightarrow - \frac{\pi }{6} \le k\pi \le \frac{{5\pi }}{6} \Leftrightarrow - \frac{1}{6} \le k \le \frac{5}{6} \Rightarrow k = 0\) (vì \(k \in \mathbb{Z}\)).
Suy ra \(x = \frac{\pi }{6} + 0.\pi = \frac{\pi }{6}\).
+) \(0 \le x \le \pi \Rightarrow 0 \le - \frac{\pi }{6} + k\pi \le \pi \Leftrightarrow \frac{\pi }{6} \le k\pi \le \frac{{7\pi }}{6} \Leftrightarrow \frac{1}{6} \le k \le \frac{7}{6} \Rightarrow k = 1\) (vì \(k \in \mathbb{Z}\)).
Suy ra \(x = - \frac{\pi }{6} + 1.\pi = \frac{{5\pi }}{6}\).
Vậy trên đoạn \(\left[ {0;\pi } \right]\) thì f’(x) = 0 có hai nghiệm là \(x = \frac{\pi }{6}\); \(x = \frac{{5\pi }}{6}\).
d) Đúng. f(x) = x – sin2x;
f’(x) = 1 – 2cos2x có nghiệm \(x = \frac{\pi }{6}\); \(x = \frac{{5\pi }}{6}\) thuộc \(\left[ {0;\pi } \right]\).
\(f\left( 0 \right) = 0\); \(f\left( \pi \right) = \pi \); \(f\left( {\frac{\pi }{6}} \right) = \frac{\pi }{6} - \frac{{\sqrt 3 }}{2}\); \(f\left( {\frac{{5\pi }}{6}} \right) = \frac{{5\pi }}{6} + \frac{{\sqrt 3 }}{2}\).
Vậy giá trị nhỏ nhất của f(x) trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) là \(\frac{\pi }{6} - \frac{{\sqrt 3 }}{2}\).

Các bài tập cùng chuyên đề
Bài 1 :
Cho hàm số \(y = {x^2} - 4x + 3\). Thực hiện lần lượt các yêu cầu sau:
a) Tính y’ và tìm các điểm tại đó \(y' = 0\).
b) Xét dấu y’ để tìm các khoảng đồng biến, khoảng nghịch biến và cực trị của hàm số.
c) Tính \(\mathop {\lim }\limits_{x \to - \infty } y\), \(\mathop {\lim }\limits_{x \to + \infty } y\) và lập bảng biến thiên của hàm số.
d) Vẽ đồ thị của hàm số và nhận xét về tính đối xứng của đồ thị.
Bài 2 :
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a) \(y = - {x^3} + 6{x^2} - 9x + 12\);
b) \(y = \frac{{2x - 1}}{{x + 1}}\);
c) \(y = \frac{{{x^2} - 2x}}{{x - 1}}\).
Bài 3 :
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a) \(y = {x^3} - 3{x^2}\);
b) \(y = \frac{{2x + 1}}{{x + 2}}\);
c) \(y = \frac{{2{x^2} + x - 2}}{{x - 1}}\).
Bài 4 :
Một tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm ở độ cao 250km so với bề mặt của Mặt Trăng.
Trong khoảng 50 giây đầu tiên kể từ khi đốt cháy các tên lửa hãm độ cao hát của con tàu so với bề mặt của mặt trăng được tính gần đúng bởi hàm:
\(h\left( t \right) = - 0,01{t^3} + 1,1{t^2} - 30t + 250\)
Trong đó t là thời gian tính bằng giây và h là độ cao tính bằng kilômét.
a) Tìm thời điểm t (0 ≤ t ≤ 70) sao cho con tàu đạt khoảng cách nhỏ nhất so với bề mặt của Mặt Trăng. Khoảng cách nhỏ nhất này là bao nhiêu?
b) Vẽ đồ thị của hàm số y = h(t) với 0 ≤ t ≤ 70 (đơn vị trên trục hoành là 10 giây, đơn vị trên trục tung là 50 km).
c) Gọi v(t) là vận tốc tức thời của con tàu ở thời điểm t (giây) kể từ khi đốt cháy các tên lửa hãm với 0 ≤ t ≤ 70. Xác định hàm số v(t).
d) Vận tốc tức thời của con tàu lúc bắt đầu hãm phanh là bao nhiêu? Tại thời điểm t = 25 (giây) là bao nhiêu?
e) Tại thời điểm t = 25 (giây), vận tốc tức thời của con tàu vẫn giảm hay đang tăng trở lại?
Bài 5 :
Xét phản ứng hoá học tạo ra chất C từ hai chất A và B:
\(A+ B\to C\).
Giả sử nồng độ của hai chất A và B bằng nhau [A] = [B] = a (mol/l). Khi đó, nồng độ của chất C theo thời gian t (t > 0) được cho bởi công thức: \(\left[ C \right] = \frac{{{a^2}Kt}}{{aKt + 1}}\) (mol/l), trong đó K là hằng số dương.
a) Tìm tốc độ phản ứng ở thời điểm t > 0.
b) Chứng minh nếu \(x = \left[ C \right]\) thì \(x'(t) = K{(a - x)^2}\).
c) Nêu hiện tượng xảy ra với nồng độ các chất khi \(t \to + \infty \).
d) Nêu hiện tượng xảy ra với tốc độ phản ứng khi \(t \to + \infty \).
Bài 6 :
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau
a,\(y = {x^3} - 3{x^2} + 2\)
\(b,\;y = - {x^3} + 3{x^2} - 6x\)
\(c,y = \frac{{3x - 2}}{{x - 2}}\)
\(d,y = \frac{x}{{2x + 3}}\)
\(e,y = \frac{{{x^2} + 2x + 4}}{x}\)
\(g,y = \frac{{{x^2} + 4x + 3}}{{x + 2}}\;\)
Bài 7 :
Trong một nhà hàng, mỗi tuần để chế biến x phần ăn (x lấy giá trị trong khoảng từ 30 đến 120) thì chi phí trung bình (đơn vị: nghìn đồng) của một phần ăn được cho bởi công thức:
\(\overline C (x) = 2x - 230 + \frac{{7200}}{x}\)
a) Khảo sát và vẽ đồ thị hàm số \(\overline C (x)\) trên [30; 120].
b) Từ kết quả trên, tìm số phần ăn sao cho chi phí trung bình của một phần ăn là thấp nhất.
Bài 8 :
Điện trở R (\(\Omega \)) của một đoạn dây dẫn hình trụ được làm từ vật liệu có điện trở suất \(\rho \)(\(\Omega \)m), chiều dài \(\ell \)(m) và tiết diện S (\({m^2}\)) được cho bởi công thức
\(R = \rho \frac{\ell }{S}\)

(Vật lí 11 – Chân trời sáng tạo, Nhà xuất bản Giáo dục Việt Nam, 2023, trang 104)
Giả sử người ta khảo sát sự biến thiên của điện trở R theo tiết diện S (ở nhiệt độ \(20^\circ C\)) của một sợi dây điện dài 10m làm từ kim loại có điện trở suất \(\rho \) và thu được đồ thị hàm số như Hình 6.
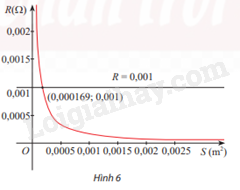
a) Có nhận xét gì về sự biến thiên của điện trở R theo tiết diện S?
b) Từ đồ thị, hãy giải thích ý nghĩa của toạ độ giao điểm của đồ thị hàm số với đường thẳng R = 0,001.
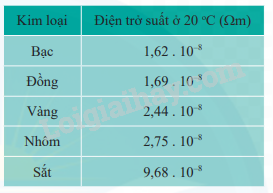
c) Tính điện trở suất \(\rho \) của dây điện. Từ đó, hãy cho biết dây điện được làm bằng kim loại nào trong số các kim loại được cho ở bảng sau:
Bài 9 :
Đường cong dưới đây là đồ thị hàm số nào?
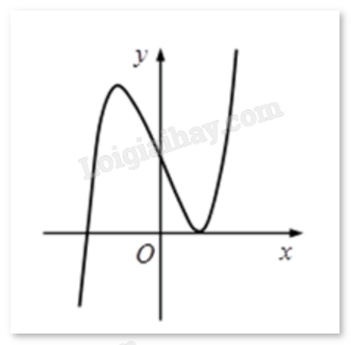
-
A.
\(y = {x^3} - 3x + 2\)
-
B.
\(y = - {x^3} - {x^2} + 1\)
-
C.
\(y = {x^2} + x + 1\)
-
D.
\(y = - {x^3} - 3x + 2\)
Bài 10 :
Quan sát bảng biến thiên và cho biết bảng biến thiên đó là của hàm số nào.
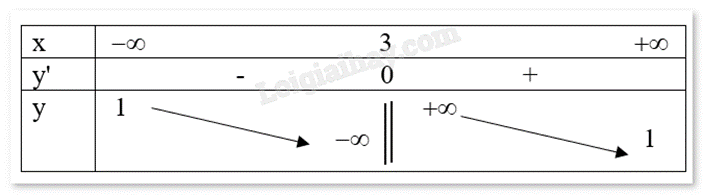
-
A.
\(y = \frac{{x - 2}}{{x - 3}}\)
-
B.
\(y = \frac{{x - 3}}{{x - 2}}\)
-
C.
\(y = \frac{{x - 2}}{{x + 3}}\)
-
D.
\(y = \frac{{3x - 2}}{{x - 1}}\)
Bài 11 :
Đồ thị dưới đây là của hàm số nào?
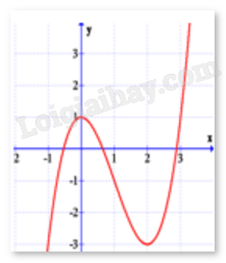
-
A.
\(y = - \frac{{{x^3}}}{3} + {x^2} + 1\)
-
B.
\(y = - {x^3} - 3{x^2} + 1\)
-
C.
\(y = 2{x^3} - 6{x^2} + 1\)
-
D.
\(y = {x^3} - 3{x^2} + 1\)
Bài 12 :
Cho hàm số \({e^x} - 2x + 3\).
a) Hàm số đã cho nghịch biến trên R
b) Hàm số đã cho đạt cực tiểu tại x = ln2
c) Đồ thị hàm số cắt trục tung tại điểm có tọa độ (0;4)
d) Đồ thị hàm số đã cho không đi qua gốc tọa độ
Bài 13 :
Đồ thị của hàm số nào dưới đây có dạng như trong hình dưới?
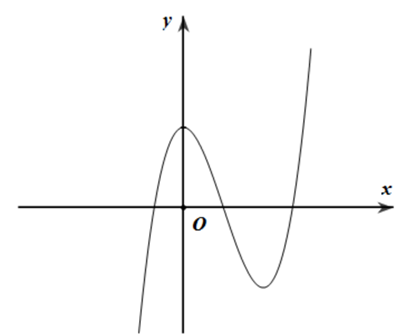
-
A.
\(y = {x^3} - 3{x^2} + 2\)
-
B.
\(y = - {x^3} + 3{x^2} + 2\)
-
C.
\(y = {x^3} + 3{x^2} + 2\)
-
D.
\(y = - {x^3} - 3{x^2} + 2\)
Bài 14 :
Cho hàm số \(f(x) = a{x^3} + b{x^2} + cx + d\) có bảng biến thiên như hình vẽ:

Xác định công thức của hàm số.
-
A.
\(y = {x^3} - 3{x^2} + 1\)
-
B.
\(y = - {x^3} - 3{x^2} + 1\)
-
C.
\(y = {x^3} - 3{x^2} + 2\)
-
D.
\(y = - {x^3} - 3{x^2} - 1\)
Bài 15 :
Cho hàm số f(x) xác định trên R có bảng biến thiên như sau:
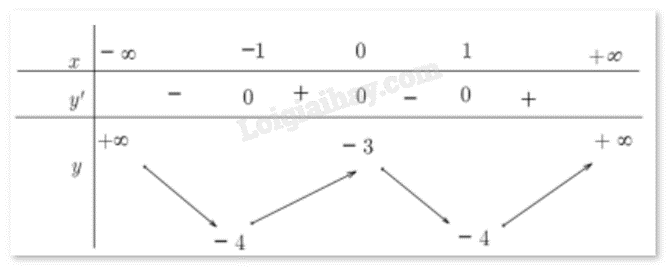
a) Hàm số f(x) đồng biến trên mỗi khoảng (-1;0) và (0;1)
b) Số điểm cực trị của hàm số đã cho là 3
c) Hàm số f(x) có giá trị lớn nhất bằng -3
d) Đồ thị hàm số không có đường tiệm cận
Bài 16 :
Cho hàm số \(y=x - \sqrt {{x^2} + 1} \).
a) Hàm số đã cho nghịch biến trên R
b) Đồ thị hàm số đã cho có cực tiểu
c) Đồ thị hàm số đã cho có 1 tiệm cận ngang
d) Đồ thị hàm số đã cho không đi qua gốc tọa độ
Bài 17 :
Đường cong hình bên là đồ thị của hàm số nào trong bốn hàm số dưới đây?
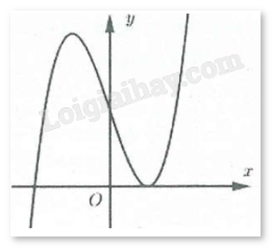
-
A.
\(y = {x^3} - 3{x^2} + 2\)
-
B.
\(y = {x^2} - x + 1\)
-
C.
\(y = \frac{{x + 3}}{{x - 2}}\)
-
D.
\(y = - {x^3} + 3{x^2} + 2\)
Bài 18 :
Cho hàm số f(x) xác định trên R có bảng biến thiên như sau:
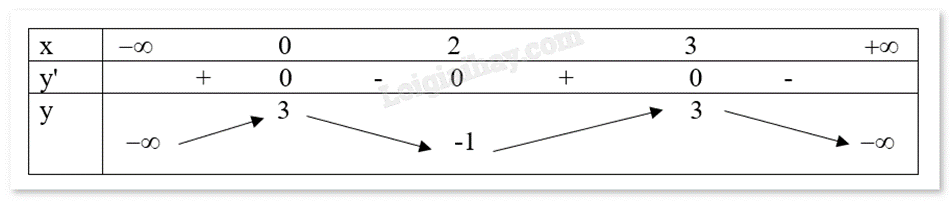
a) Hàm số f(x) đồng biến trên mỗi khoảng (0;2) và (2;3)
b) Số điểm cực trị của hàm số đã cho là 3
c) Hàm số f(x) có giá trị lớn nhất bằng 3
Hàm số đạt cực tiểu tại x = -1
d) Hàm số đạt cực tiểu tại x = -1
Bài 19 :
Cho hàm số \(f(x) = - {x^4} + 12{x^2} + 1\).
a) Hàm số f(x) đồng biến trên khoảng (1;37)
b) Số điểm cực trị của hàm số đã cho là 3
c) Hàm số f(x) có giá trị nhỏ nhất trên đoạn [-1;2] bằng 12
d) Hàm số f(x) có giá trị lớn nhất trên đoạn [-1;2] bằng 33
Bài 20 :
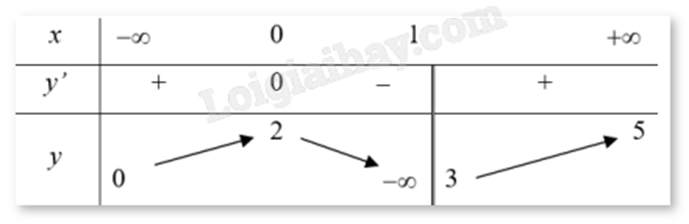
Cho hàm số y = f(x) là hàm số xác định trên R∖{1}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau. Mệnh đề nào dưới đây đúng?
-
A.
Đồ thị hàm số có hai tiệm cận ngang là y = 0, y = 5 và tiệm cận đứng là x = 1
-
B.
Giá trị cực tiểu của hàm số là y = 3
-
C.
Giá trị cực đại của hàm số 5
-
D.
Đồ thị hàm số có 2 đường tiệm cận
Bài 21 :
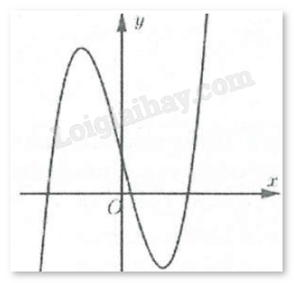
Đường cong hình bên là đồ thị của hàm số nào trong bốn hàm số dưới đây?
-
A.
\(y = {x^3} - 4x + 1\)
-
B.
\(y = {x^3} + 3{x^2} + 1\)
-
C.
\(y = {x^3} - 4x - 1\)
-
D.
\(y = - {x^3} + 4x + 1\)
Bài 22 :
Cho hàm số f(x) xác định trên R có bảng biến thiên như sau:
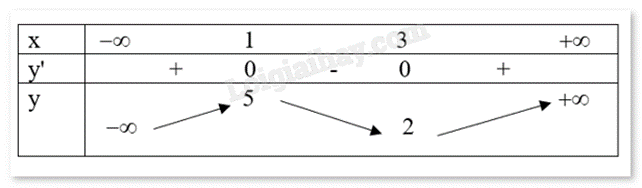
a) Hàm số f(x) đồng biến trên mỗi khoảng \(( - \infty ;1)\) và \((3; + \infty )\)
b) Số điểm cực trị của hàm số đã cho là 2
c) Hàm số f(x) có giá trị lớn nhất bằng 5
d) Hàm số đạt cực tiểu tại x = 2
Bài 23 :
Cho hàm số \(f(x) = {x^3} - 24x\).
a) Hàm số f(x) đồng biến trên khoảng \(( - \infty ;0)\).
b) Đồ thị hàm số có điểm cực tiểu là (16;-2048).
c) Hàm số f(x) có giá trị lớn nhất trên đoạn [2;19] bằng 6403.
d) Hàm số f(x) có giá trị nhỏ nhất trên đoạn [2;19] bằng -40.
Bài 24 :
Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào sau đây?
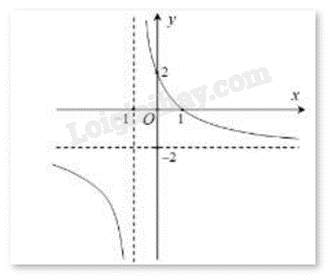
-
A.
\(y = \frac{{2 - 2x}}{{x + 1}}\)
-
B.
\(y = 2{x^3} - x + 1\)
-
C.
\(y = \frac{{ - 2x + 1}}{{x + 2}}\)
-
D.
\(y = {x^4} + 2{x^2} + 2\)
Bài 25 :
Đường cong hình bên là đồ thị của hàm số nào trong bốn hàm số dưới đây?
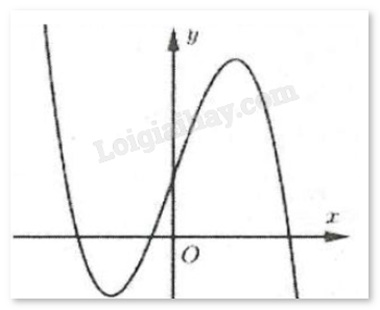
-
A.
\(y = - {x^3} + 3{x^2} + 1\)
-
B.
\(y = - {x^3} + 3x + 1\)
-
C.
\(y = {x^3} - 3x + 1\)
-
D.
\(y = - {x^3} - 3x + 1\)
Bài 26 :
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ sau:
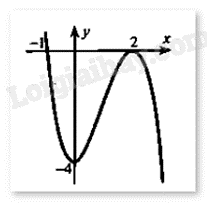
-
A.
\(y = {x^3} + 3{x^2} - 4\)
-
B.
\(y = - {x^3} + 3{x^2} + 4\)
-
C.
\(y = {x^3} + 3{x^2} + 4\)
-
D.
\(y = - {x^3} + 3{x^2} - 4\)
Bài 27 :
Cho hàm số f(x) xác định trên R\{3} có bảng biến thiên như sau:
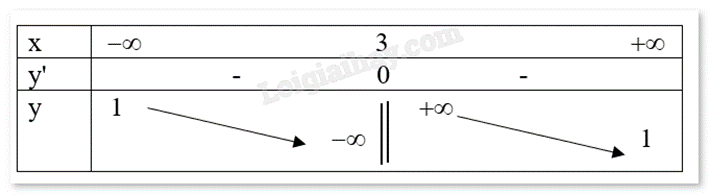
a) Hàm số f(x) đồng biến trên mỗi khoảng xác định
b) Số điểm cực trị của hàm số đã cho là 1
c) Hàm số f(x) có giá trị lớn nhất bằng 1
d) Đồ thị hàm số f(x) có hai đường tiệm cận
Bài 28 :
Cho hàm số \(f(x) = {x^4} - 10{x^2} - 4\).
a) Hàm số f(x) nghịch biến trên khoảng
b) Hàm số có 3 điểm cực trị
c) Hàm số f(x) có giá trị lớn nhất trên đoạn [0;9] bằng -4
d) Hàm số f(x) có giá trị nhỏ nhất trên đoạn [2;19] bằng -29
Bài 29 :
Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào sau đây?
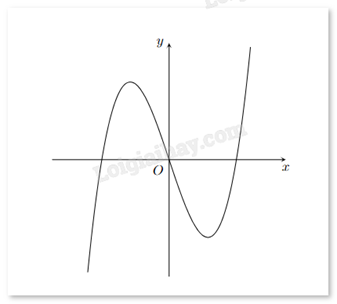
-
A.
\(y = \frac{{2x + 1}}{{x - 1}}\)
-
B.
\(y = {x^3} - 3x\)
-
C.
\(y = - {x^4} + 2{x^2} - 1\)
-
D.
\(y = - {x^3} - 3x\)
Bài 30 :
Tọa độ tâm đối xứng của đồ thị hàm số \(y = {x^3} + 3{x^2} - 9x + 1\) là:
-
A.
(-1;6)
-
B.
(-1;12)
-
C.
(1;4)
-
D.
(-3;28)












