Nội dung từ Loigiaihay.Com
Giả sử tỉ lệ sinh của tỉnh A tuân theo quy luật logistic được mô hình hoá bằng hàm số \(f(t) = \frac{{200}}{{1 + 4{e^{ - t}}}}\), \(t \ge 0\), \(t \in \mathbb{N}\), trong đó thời gian t được tính bằng tháng. Khi đó đạo hàm f’(t) sẽ biểu thị tốc độ tăng dân số của tỉnh A. Hỏi sau bao nhiêu tháng tốc độ tăng trưởng của dân số tỉnh A là lớn nhất?
Đáp án:
Đáp án:
Tính đạo hàm cấp hai của f(t), từ đó tìm giá trị lớn nhất của f’(t).
\(f'(t) = 200.\frac{{ - 4{e^{ - t}}}}{{{{(1 + 4{e^{ - t}})}^2}}} = \frac{{800{e^{ - t}}}}{{{{(1 + 4{e^{ - t}})}^2}}}\);
\(f''(t) = 800.\frac{{ - {e^{ - t}}{{(1 + 4{e^{ - t}})}^2} - {e^{ - t}}.2.( - 4{e^{ - t}}).(1 + 4{e^{ - t}})}}{{{{(1 + 4{e^{ - t}})}^4}}} = 800.\frac{{4{{({e^{ - t}})}^2} - {e^{ - t}}}}{{{{(1 + 4{e^{ - t}})}^3}}} = \frac{{800{e^{ - t}}}}{{{{(1 + 4{e^{ - t}})}^3}}}(4{e^{ - t}} - 1)\).
\(f''(t) = 0 \Leftrightarrow 4{e^{ - t}} - 1 = 0 \Leftrightarrow \ln {e^{ - t}} = \ln \frac{1}{4} \Leftrightarrow - t\ln e = \ln 1 - \ln 4 \Leftrightarrow - t = 0 - \ln 4 \Leftrightarrow t = \ln 4\).
Bảng biến thiên:
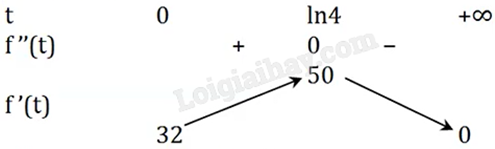
Giá trị lớn nhất của f’(t) là f’(ln4) = 50.
Tốc độ tăng trưởng dân số của tỉnh A lớn nhất bằng 50 khi \(t = \ln 4 \approx 1,38\).
\(f'(1) \approx 48,18\); \(f'(2) \approx 45,57\). Suy ra f’(1) > f’(2).
Vậy sau 1 tháng, tốc độ tăng trưởng dân số của tỉnh A là lớn nhất.

Các bài tập cùng chuyên đề
Bài 1 :
Khi máu di chuyển từ tim qua các động mạch chính rồi đến các mao mạch và quay trở lại qua các tĩnh mạch, huyết áp tâm thu (tức là áp lực của máu lên động mạch khi tim co bóp) liên tục giảm xuống. Giả sử một người có huyết áp tâm thu P (tính bằng mmHg) được cho bởi hàm số \(P\left( t \right) = \frac{{25{t^2} + 125}}{{{t^2} + 1}},0 \le t \le 10\), trong đó thời gian t được tính bằng giây. Tính tốc độ thay đổi của huyết áp sau 5 giây kể từ khi máu rời tim.
Bài 2 :
Giả sử một hạt chuyển động trên một trục thẳng đứng chiều dương hướng lên trên sao cho tọa độ của hạt (đơn vị: mét) tại thời điểm t (giây) là \(y = {t^3} - 12t + 3,t \ge 0\).
a) Tìm các hàm vận tốc và gia tốc.
b) Khi nào thì hạt chuyển động lên trên và khi nào thì hạt chuyển động xuống dưới?
c) Tìm quãng đường hạt đi được trong khoảng thời gian \(0 \le t \le 3\).
d) Khi nào hạt tăng tốc? Khi nào hạt giảm tốc?
Bài 3 :
Giả sử chi phí (tính bằng trăm nghìn đồng) để sản xuất x đơn vị hàng hóa nào đó là: \(C\left( x \right) = 23\;000 + 50x - 0,5{x^2} + 0,00175{x^3}\)
a) Tìm hàm chi phí biên.
b) Tìm C’(100) và giải thích ý nghĩa của nó.
c) So sánh C’(100) với chi phí sản xuất đơn vị hàng hóa thứ 101.
Bài 4 :
Một chất điểm chuyển động có phương trình chuyển động là \(s(t) = - {t^3} + 6{t^2} + 5t\), với t (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong khoảng thời gian đó. Trong khoảng thời gian 5 giây đầu tiên, vận tốc của chất điểm đạt giá trị lớn nhất là bao nhiêu?
-
A.
19
-
B.
5
-
C.
17
-
D.
10
Bài 5 :
Một vật chuyển động theo quy luật \(s = - 2{t^3} + 18{t^2}\) với t (giây) là khoảng thời gian từ khi vật bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển trong thời gian đó. Hỏi trong khoảng thời gian 6 giây kể từ lúc bắt đầu chuyển động, vật đạt vận tốc lớn nhất tại thời điểm nào?
-
A.
2
-
B.
3
-
C.
4
-
D.
6
Bài 6 :
Một chất điểm chuyển động theo phương trình \(s(t) = -\frac{1}{3}{t^3} + 18{t^2} - 35t + 10\), trong đó t tính bằng giây, s tính bằng mét. Trong 40 giây đầu tiên, chất điểm đó có vận tốc tức thời giảm trong khoảng thời gian (a;b). Tính giá trị biểu thức P = a + 9b.
Bài 7 :
Dân số của một quốc gia sau t năm kể từ năm 2023 được ước tính bởi công thức \(N(t) = 100{e^{0,012t}}\) (N(t) được tính bằng triệu người), \(0 \le t \le 50\)). Đạo hàm của hàm số N(t) biểu thị tốc độ tăng trưởng dân số của quốc gia đó (tính bằng triệu người/năm). Vào năm nào tốc độ tăng trưởng dân số của quốc gia đó là 1,5 triệu người/năm?
Bài 8 :
Trong một thí nghiệm y học, người ta cấy 1 000 con vi khuẩn vào môi trường dinh dưỡng. Bằng thực nghiệm, người ta xác định được số lượng vi khuẩn thay đổi theo thời gian bởi công thức:
\(N\left( t \right) = 1000 + \frac{{100t}}{{100 + {t^2}}}\)
trong đó \(t\) là thời gian tính bằng giây \(\left( {t \ge 0} \right)\) (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014). Trong khoảng thời gian nào từ lúc nuôi cấy, số lượng vi khuẩn sẽ tăng lên?
Bài 9 :
Trong 5 giây đầu tiên, một chất điểm chuyển động theo phương trình
\(s\left( t \right) = {t^3} - 6{t^2} + 14t + 1\)
trong đó \(t\) tính bằng giây và \(s\) tính bằng mét. Trong khoảng thời gian nào của 5 giây đầu tiên thì vận tốc tức thời của chất điểm tăng lên?
Bài 10 :
Độ cao (tính bằng mét) của tàu lượn siêu tốc so với mặt đất sau \(t\)(giây) \(\left( {0 \le t \le 20} \right)\) từ lúc bắt đầu được cho bởi công thức
\(h\left( t \right) = - \frac{4}{{255}}{t^3} + \frac{{49}}{{85}}{t^2} - \frac{{98}}{{17}}t + 20\).
Trong khoảng thời gian nào tàu lượn đi xuống, trong khoảng thời gian nào tàu lượn đi lên?
Bài 11 :
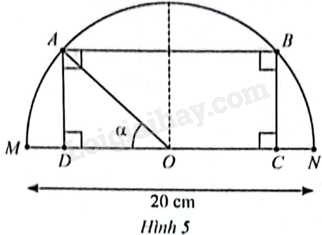
Cho điểm \(A\) di động trên nửa đường tròn tâm \(O\) đường kính \(MN = 20{\rm{ }}cm,\widehat {MOA} = \alpha \) với \(0 \le \alpha \le \pi \). Lấy điểm \(B\) thuộc nửa đường tròn và \(C,D\) thuộc đường kính \(MN\) được xác định sao cho \(ABCD\) là hình chữ nhật. Khi \(A\) di động từ trái sang phải, trong các khoảng nào của \(\alpha \) thì diện tích của hình chữ nhật \(ABCD\) tăng, trong các khoảng nào của \(\alpha \) thì diện tích của hình chữ nhật \(ABCD\) giảm?
Bài 12 :
Một cửa hàng ước tính số lượng sản phẩm \(q\left( {0 \le q \le 100} \right)\) bán được phụ thuộc vào giá bán \(p\) (tính bằng nghìn đồng) theo công thức \(p + 2q = 300\). Chi phí cửa hàng cần chi để nhập về \(q\) sản phẩm là
\(C\left( q \right) = 0,05{q^3} - 5,7{q^2} + 295q + 300\) (nghìn đồng).
a) Viết công thức tính lợi nhuận \(I\) của cửa hàng khi nhập về và bán được \(q\) sản phẩm.
b) Trong khoảng nào của \(q\) thì lợi nhuận sẽ tăng khi \(q\) tăng, trong khoảng nào thì lợi nhuận giảm khi \(q\) tăng?
Bài 13 :
Doanh số bán hệ thống âm thanh nổi mới trong khoảng thời gian dự kiến sẽ tuân theo đường cong logistic \(R = R\left( x \right) = \frac{{5000}}{{1 + 5{e^{ - x}}}},x \ge 0\), trong đó thời gian \(x\) được tính bằng năm. Hỏi tốc độ bán hàng đạt tối đa vào năm nào?
Bài 14 :
Ở \({0^ \circ }C\), sự mất nhiệt \(H\) (tính bằng Kcal/m2h, ở đây Kcal là kilocalories và 1 Kcal=1000 calo) từ cơ thể của một người có thể được mô hình hóa bằng công thức
\(H = 33\left( {10\sqrt v - v + 10,45} \right),\)
Trong đó \(v\) là tốc độ gió (tính bằng m/s) (Theo sách Brief Calculus: An Applied Approach, 8th edition, Cengage Learning, 2009).
a) Xét tính đơn điệu của hàm số \(H\) và giải thích ý nghĩa thực tiễn của kết quả nhận được.
b) Tìm tốc độ thay đổi của \(H\) khi \(v = 2\) m/s. Giải thích ý nghĩa thực tiễn của kết quả này.
Bài 15 :
Thể tích \(V\) của 1 kg nước (tính bằng cm3) ở nhiệt độ \(T\) (đơn vị: oC) khi \(T\) thay đổi từ 0oC đến 30oC được cho xấp xỉ bởi công thức:
\(V = 999,87 - 0.06426T + 0,0085043{T^2} - 0,0000769{T^3}\)
(Nguồn: James Stewart,J(2015).Calculus.Cengage Learning 8th edition, p.284)
Tìm nhiệt độ \({T_0} \in (0;30)\) kể từ nhiệt độ \({T_0}\) trở lên thì thể tích tăng (làm tròn kết quả đến hàng đơn vị).
Bài 16 :
Một công ty tiến hành khai thác 17 giếng dầu trong khi vực được định. Trung bình mỗi giếng dầu chiết xuất đc 245 thùng dầu mỗi ngày. Công ty có thể khai thác nhiều hơn 17 giếng dầu nhưng cứ khai thác thêm một giếng thì lượng dầu mỗi giếng chiết xuất được hằng ngày giảm 9 thùng. Để giám đóc công ty có thể quyết định số giếng cần thêm cho phù hợp với tài chính, hãy chỉ ra số giếng công ty có thể khai thác thêm để sản lượng dầu chiết xuất tăng lên.
Bài 17 :
Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhận đầu tiên đến ngày thứ t là \(f(t) = 45{t^2} - {t^3}\), t = 0, 1, 2, …, 25. Nếu coi f là hàm số xác định trên [0;25] thì f’(t) được xem là tốc độ truyền bệnh (người/ngày) tại thời điểm t. Xác định ngày mà tốc độ truyền bệnh là lớn nhất.
Bài 18 :
Giả sử số lượng của một quần thể nấm X tại môi trường nuôi cấy trong phòng thí nghiệm được mô hình hóa bằng hàm số \(P(t) = 120{e^{0,15t}}\), trong đó thời gian t được tính bằng giờ. Tại thời điểm ban đầu t = 0, tốc độ tăng trưởng của quần thể nấm X là bao nhiêu (đơn vị: tế bào/giờ)?
Bài 19 :
Một vật chuyển động với vận tốc ban đầu là \( v_0 \) (m/s) sau đó dừng lại, phương trình quãng đường của vật là \( s = s(t) = -t^3 + 6t^2 + 15t \) trong đó t tính bằng giây và s tính bằng mét.
Vận tốc của vật tại thời điểm t = 2 s là v = 18 m/s.
Vận tốc của vật tại thời điểm t là \( v(t) = -3t^2 + 12t + 15 \) (m/s).
Vật đạt vận tốc lớn nhất tại thời điểm t = 2(s).
Vật dừng lại sau khoảng thời gian kể từ lúc bắt đầu chuyển động là t = 4s giây.
Bài 20 :
Giả sử lợi nhuận biên (tính bằng triệu đồng) của một sản phẩm được mô hình hóa bằng công thức P'(x) = −0,0004x + 9,3. Ở đây P(x) là lợi nhuận (tính bằng triệu đồng) khi bán được x đơn vị sản phẩm. Khi đó sự thay đổi của lợi nhuận khi doanh số tăng từ 100 lên 125 đơn vị sản phẩm là
-
A.
232,325 triệu đồng
-
B.
230,315 triệu đồng
-
C.
321,385 triệu đồng
-
D.
231,375 triệu đồng
Bài 21 :
Sự ảnh hưởng khi sử dụng một loại độc tố với vi khuẩn X được một nhà sinh học mô tả bởi hàm số \(P(t) = \frac{{t + 1}}{{{t^2} + t + 4}}\), trong đó P(t) là số lượng vi khuẩn sau t giờ sử dụng độc tố. Hỏi sau bao nhiêu giờ thì số lượng vi khuẩn X bắt đầu giảm?
Bài 22 :
Thể tích nước của một bể bơi sau $t$ phút bơm được tính theo công thức $V(t) = \frac{1}{100} (-0,5t^3 + 90t^2)$, $(m^3)$ $(0 \leq t \leq 120)$. Tốc độ bơm nước tại thời điểm $t$ được tính bởi $v(t) = V'(t)$. Xét tính đúng sai các mệnh đề sau:
a) Thể tích nước sau 10 phút là 80 $m^3$.
b) Tốc độ bơm nước tại thời điểm $t = 20$ phút là 30 ($m^3$/phút).
c) Trong 30 phút đầu thể tích nước lớn nhất trong bể là 675 $m^3$.
d) Tốc độ bơm nước cao nhất là 60 ($m^3$/phút).
Bài 23 :
Đậu đỏ là một loại thực phẩm quen thuộc trong bữa ăn của người Việt Nam. Ngoài giá trị dinh dưỡng cao, đậu đỏ còn có nhiều công dụng tuyệt vời cho sức khỏe và sắc đẹp như: chống oxy hóa, giúp cơ bắp con người khỏe mạnh, tăng cường sức khỏe cho tim mạch con người, lợi ích cho hệ tiêu hóa, bổ thận, cung cấp vitamin bổ dưỡng cho cơ thể, đào thải độc tố, giải độc, tốt cho hệ miễn dịch, giúp huyết áp ổn định, da đẹp. Cây đậu đỏ khi trồng có chiều cao 6 centimet. Khảo sát cho thấy độ cao tính bằng centimet của cây đậu đỏ tại thời điểm t kể từ khi được trồng được cho bởi hàm số $h(t) = - 0,005t^{4} + bt^{3} + c$ (trong đó $b,\, c \in {\mathbb{R}}$), với t tính theo tuần. Giả sử h’(t) là tốc độ tăng chiều cao của cây đậu đỏ sau khi trồng (đơn vị của h’(t): centimet/tuần). Biết h’(5) = 5 (Hình bên dưới mô tả hạt và cây đậu đỏ).

a) Hàm số h(t) có công thức $h(t) = - 0,005t^{4} + 0,1t^{3}$.
b) Giai đoạn tăng trưởng của cây đậu đỏ đó kéo dài 15 tuần.
c) Chiều cao tối đa của cây đậu đỏ đó là 90 centimet.
d) Vào thời điểm cây đậu đỏ đó phát triển nhanh nhất thì chiều cao của cây là 56 centimet.












