Nội dung từ Loigiaihay.Com
Cho đường tròn \(\left( O \right)\). Biết \(MA;MB\) là các tiếp tuyến của \(\left( O \right)\) cắt nhau tại \(M\) và \(\widehat {AMB} = 58^\circ \) Khi đó số đo \(\widehat {ABO}\) bằng:
-
A.
\(24^\circ \).
-
B.
\(29^\circ \).
-
C.
\(30^\circ \).
-
D.
\(31^\circ \).
Chứng minh tam giác AMO, BMO nội tiếp đường tròn nên tứ giác AMBO nội tiếp đường tròn.
Sử dụng định lí tổng hai góc đối của tứ giác nội tiếp để tính góc AOB.
Sử dụng định lí tổng ba góc của tam giác bằng \(180^\circ \) và tính chất tam giác cân để tính \(\widehat {ABO}\).
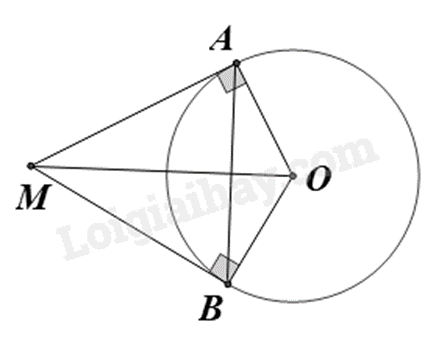
Vì MA; MB là các tiếp tuyến của (O) nên \(MA \bot OA,MB \bot OB\).
Do đó \(\Delta AMO;\Delta BMO\) lần lượt vuông tại A và B, do đó \(\Delta AMO;\Delta BMO\) ngoại tiếp đường tròn đường kính OM hay 4 điểm A, M, B, O thuộc cùng một đường tròn.
Do đó AMBO là tứ giác nội tiếp.
Áp dụng định lí tổng hai góc đối của tứ giác nội tiếp, ta có: \(\widehat {AMB} + \widehat {AOB} = 180^\circ \).
Suy ra \(\widehat {AOB} = 180^\circ - \widehat {AMB} = 180^\circ - 58^\circ = 122^\circ \)
Tam giác AOB cân tại O (do OA = OB) nên \(\widehat {ABO} = \frac{{180^\circ - \widehat {AOB}}}{2} = \frac{{180^\circ - 122^\circ }}{2} = 29^\circ \).
Đáp án B
Đáp án : B

Các bài tập cùng chuyên đề
Bài 1 :
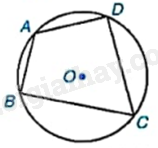
Cho tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) (hình \(1\) ). Chọn khẳng định sai?
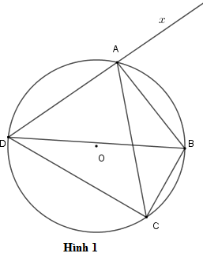
-
A.
\(\widehat {BDC} = \widehat {BAC}\)
-
B.
\(\widehat {ABC} + \widehat {ADC} = 180^\circ \)
-
C.
\(\widehat {DAB} = \widehat {BAx}\)
-
D.
\(\widehat {BCA} = \widehat {BDA}\)
Bài 2 :
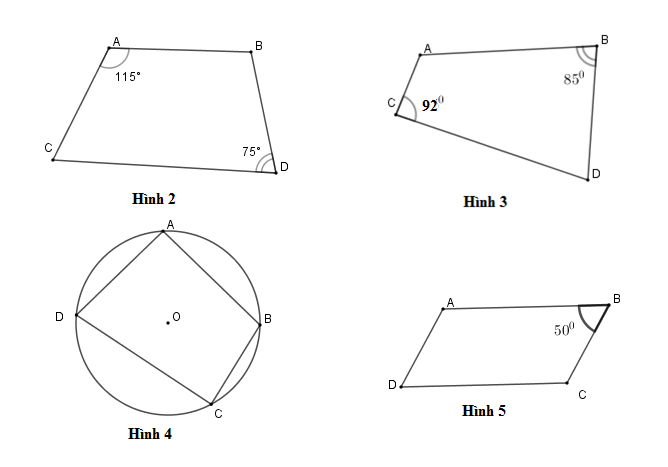
Tứ giác ở hình nào dưới đây là tứ giác nội tiếp?
-
A.
Hình $2$
-
B.
Hình $3$
-
C.
Hình $4$
-
D.
Hình $5$
Bài 3 :
Tứ giác $ABCD$ nội tiếp đường tròn có hai cạnh đối $AB$ và $CD$ cắt nhau tại $M$ và $\widehat {BAD} = {70^0}$ thì $\widehat {BCM} = ?$
-
A.
\({110^0}\)
-
B.
\({30^0}\)
-
C.
\({70^0}\)
-
D.
\({55^0}\)
Bài 4 :
Cho hình vẽ dưới đây
Bài 5 :
Cho tứ giác ABCD nội tiếp. Chọn câu sai:
-
A.
$\widehat {BAD} + \widehat {BCD} = {180^0}$
-
B.
$\widehat {ABD} = \widehat {ACD}$
-
C.
$\widehat A + \widehat B + \widehat C + \widehat D = {360^0}$
-
D.
$\widehat {ADB} = \widehat {DAC}$
Bài 6 :
Cho tứ giác ABCD có số đo các góc A, B, C, D lần lượt như sau. Trường hợp nào thì tứ giác ABCD có thể là tứ giác nội tiếp.
-
A.
${50^0};{60^0};{130^0};{140^0}$
-
B.
${65^0};{85^0};{115^0};{95^0}$
-
C.
${82^0};{90^0};{98^0};{100^0}$
-
D.
Các câu đều sai
Bài 7 :
Tứ giác $ABCD$ nội tiếp đường tròn có hai cạnh đối $AB$ và $CD$ cắt nhau tại $M$ và $\widehat {BAD} = {80^\circ}$ thì $\widehat {BCM} = ?$
-
A.
\({100^0}\)
-
B.
\({40^0}\)
-
C.
\({70^0}\)
-
D.
\({80^0}\)
Bài 8 :
Cho hình vẽ dưới đây
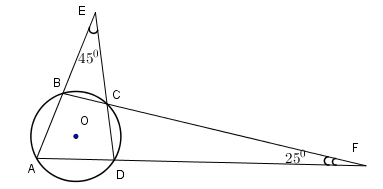
Bài 9 :
Em hãy đo các góc đối nhau A và C của tứ giác ABCD trong HĐ2 và tính tổng \(\widehat A + \widehat C\). So sánh kết quả của em với các bạn.
Bài 10 :
Cho tam giác ABC có các đường cao BE, CF. Biết rằng \(\widehat B = {60^o},\widehat C = {80^o}\).
a) Chứng tỏ rằng tứ giác BCEF nội tiếp một đường tròn có tâm là trung điểm của cạnh BC.
b) Tính số đo của các góc BFE và CEF.
Bài 11 :
Cho ABCD là tứ giác nội tiếp. Tính số đo của các góc còn lại của tứ giác trong mỗi trường hợp sau:
a) \(\widehat A = {60^o},\widehat B = {80^o}\);
b) \(\widehat B = {70^o},\widehat C = {90^o}\);
c) \(\widehat C = {100^o},\widehat D = {60^o}\);
d) \(\widehat D = {110^o},\widehat A = {80^o}\).
Bài 12 :
Cho điểm I nằm ngoài đường tròn (O). Qua I kẻ hai đường thẳng lần lượt cắt (O) tại bốn điểm A, B và C, D sao cho A nằm giữa B và I, C nằm giữa D và I. Chứng minh rằng \(\widehat {IBD} = \widehat {ICA},\widehat {IAC} = \widehat {IDB}\) và \(IA.IB = IC.ID\).
Bài 13 :
Cho hình thang ABCD (AB song song với CD) nội tiếp đường tròn (O). Chứng minh rằng ABCD là hình thang cân.
Bài 14 :
Cho tam giác ABC có các đường cao AD, BE, CF. Chứng minh rằng BCEF, CAFD, ABDE là những tứ giác nội tiếp.
Bài 15 :
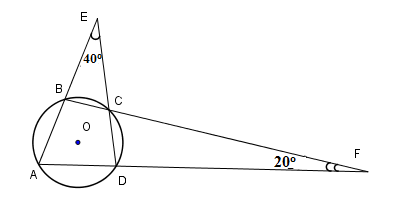
Cho tứ giác ABCD nội tiếp đường tròn (O), AB cắt CD tại E, AD cắt BC tại F như Hình 9.58. Biết \(\widehat {BEC} = {40^o}\) và \(\widehat {DFC} = {20^o}\), tính số đo các góc của tứ giác ABCD.

Bài 16 :
Cho tứ giác ABCD nội tiếp một đường tròn có \(\widehat A - \widehat C = {100^o}\). Khẳng định nào dưới đây là đúng?
A. \(\widehat A = {80^o}\).
B. \(\widehat C = {80^o}\).
C. \(\widehat B + \widehat D = {100^o}\).
D. \(\widehat A = {140^o}\).
Bài 17 :
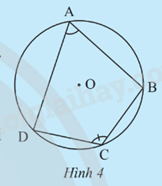
Cho tứ giác ABCD nội tiếp đường tròn (O) (Hình 4).
a) Chỉ ra các cung chắn bởi mỗi góc nội tiếp \(\widehat {DAB}\) và \(\widehat {DCB}\)
b) Tính tổng số đo của các cung vừa tìm được.
c) Nêu kết luận về tổng số đo của hai góc \(\widehat {DAB}\) và \(\widehat {DCB}\).
d) Có nhận xét gì về tổng số đo của hai góc đối diện còn lại của tứ giác ABCD?
Bài 18 :
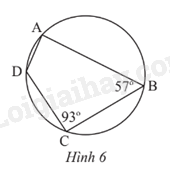
Tìm số đo các góc chưa biết của tứ giác ABCD trong Hình 6.
Bài 19 :
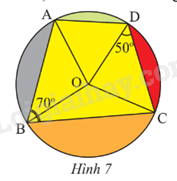
Trong hình vẽ minh họa của học sinh có một tứ giác ABCD nội tiếp đường tròn tâm O (Hình 7). Cho biết \(\widehat {ABC}\) = 70o, \(\widehat {OCD}\) = 50o. Tìm góc \(\widehat {AOD}\).
Bài 20 :
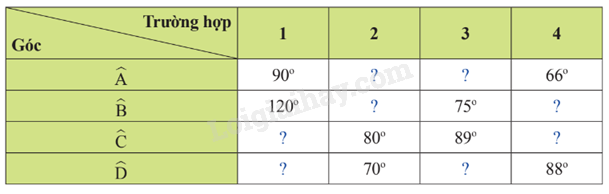
Cho ABCD là tứ giác nội tiếp. Hãy hoàn thành bảng sau vào vở.
Bài 21 :
Từ một điểm M nằm ngoài đường tròn (O), vẽ cát tuyến MBC và tiếp tuyến Mt tiếp xúc với (O) tại A. Gọi I là trung điểm của dây BC. Chứng minh AMIO là một tứ giác nội tiếp.
Bài 22 :
Cho tứ giác MNPQ nội tiếp đường tròn (O; R) và \(\widehat M\) = 60o. Số đo góc của \(\widehat P\) là
A. 30o.
B. 120o.
C. 180o.
D. 90o.
Bài 23 :
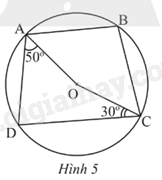
Cho tứ giác ABCD nội tiếp đường tròn (O). Biết \(\widehat {DAO}\) = 50o, \(\widehat {OCD}\) = 30o (Hình 5). Số đo của \(\widehat {ABC}\) là
A. 80o.
B. 90o.
C. 100o.
D. 110o.
Bài 24 :
Cho tứ giác ABDC nội tiếp có \(\widehat {ACD}\) = 60o. Khẳng định nào sau đây luôn đúng?
A. \(\widehat {ADC}\) = 60o.
B. \(\widehat {ADC}\) = 120o.
C. \(\widehat {ABD}\) = 60o.
D. \(\widehat {ABD}\) = 120o.
Bài 25 :
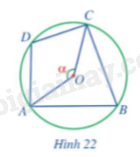
Trong Hình 22, cho biết \(\widehat {AOC} = \alpha.\)
Tính số đo của các cung và góc sau theo \( \alpha\).
a) \(\overset\frown{ADC},\widehat{ABC;}\)
b) \(\overset\frown{ADC},\widehat{ABC;}\)
c) \(\widehat{ADC}+\widehat{ABC.}\)
Bài 26 :
Cho đường tròn (O) ngoại tiếp tam giác đều ABC và điểm M thuộc cung nhỏ BC (M khác B và C). Tính số đo góc BMC.
Bài 27 :
Cho tứ giác ABCD nội tiếp đường tròn. Tính số đo các góc còn lại của tứ giác đó trong mỗi trường hợp sau:
a) \(\widehat A = 60^\circ ,\widehat B = 125^\circ .\)
b) \(\widehat B = 95^\circ ,\widehat C = 67^\circ .\)
c) \(\widehat C = 75^\circ ,\widehat D = 115^\circ .\)
d) \(\widehat D = 103^\circ ,\widehat A = 117^\circ .\)
Bài 28 :
Cho tam giác ABC nội tiếp đường tròn (O) thỏa mãn \(\widehat {ABC} = 60^\circ ,\widehat {ACB} = 70^\circ .\) Giả sử D là điểm thuộc cung BC không chứa A (D khác B và C). Tính số đo góc BDC.
Bài 29 :
Cho hình thang ABCD (AB//CD) nội tiếp đường tròn. Chứng minh rằng hình thang ABCD là hình thang cân.
Bài 30 :
Cho tứ giác nội tiếp ABCD có tam giác ABC là tam giác nhọn. Hai đường cao AM, CN của tam giác ABC cắt nhau tại H (Hình 30). Chứng minh:
a) \(\widehat {MHN} + \widehat {ABC} = 180^\circ .\)
b) \(\widehat {AHC} = \widehat {ADC.}\)
c) \(\widehat {ADC} = \widehat {BAM} + 90^\circ .\)












