Nội dung từ Loigiaihay.Com
Tính giá trị của \(x\), biết: \(x{\left( {x + 3} \right)^2} - 3x = {\left( {x + 2} \right)^3} + 1\).
(Kết quả ghi dưới dạng số thập phân)
Đáp án:
Đáp án:
Đưa phương trình về phương trình bậc nhất một ẩn để tìm x.
Ta có: \(x{\left( {x + 3} \right)^2} - 3x = {\left( {x + 2} \right)^3} + 1\)
\(\begin{array}{l}x\left( {{x^2} + 6x + 9} \right) - 3x = {x^3} + 6{x^2} + 12x + 8 + 1\\{x^3} + 6{x^2} + 9x - 3x - {x^3} - 6{x^2} - 12x - 9 = 0\\\left( {{x^3} - {x^3}} \right) + \left( {6{x^2} - 6{x^2}} \right) + \left( {9x - 3x - 12x} \right) - 9 = 0\\ - 6x = 9\\x = \frac{{ - 3}}{2} = - 1,5\end{array}\)
Vậy \(x = - 1,5\)
Đáp án: -1,5

Các bài tập cùng chuyên đề
Bài 1 :
Nghiệm của phương trình \(\frac{3}{4} + \frac{2}{5}x = 0\) có dạng \(x = - \frac{a}{b},\) trong đó \(b > 0\) và \(\frac{a}{b}\) là phân số tối giản. Khẳng định nào sau đây đúng?
-
A.
\(a + b = 21\)
-
B.
\(a + b = 23\)
-
C.
\(a + b = 20\)
-
D.
\(a + b = 24\)
Bài 2 :
Tìm x, biết rằng nếu lấy x trừ đi \(\frac{1}{4},\) rồi nhân kết quả với \(\frac{1}{2}\) thì được \(\frac{1}{8}\)
-
A.
\(x = \frac{1}{2}\)
-
B.
\(x = - \frac{1}{2}\)
-
C.
\(x = \frac{1}{4}\)
-
D.
\(x = \frac{{ - 1}}{4}\)
Bài 3 :
Gọi \({x_0}\) là nghiệm của phương trình \(3\left( {x - 5} \right) + 9x\left( {x - 3} \right) = 9{x^2}.\)
Hãy chọn đáp án đúng.
-
A.
\({x_0} < 0\)
-
B.
\({x_0} < - 1\)
-
C.
\({x_0} > 0\)
-
D.
\({x_0} > 1\)
Bài 4 :
Cho \(A = \frac{{2\left( {x + 1} \right)}}{3} - \frac{1}{2},B = \frac{{1 + 3x}}{4}\). Tìm x để \(A = B\)
-
A.
\(x = 1\)
-
B.
\(x = - 1\)
-
C.
\(x = - 2\)
-
D.
\(x = 2\)
Bài 5 :
Cho hai phương trình \(8\left( {x - 2} \right) = 14 + 6\left( {x - 1} \right) + 2\left( {x + 5} \right)\,\,\left( 1 \right)\) và \({\left( {x - 2} \right)^2} = {x^2} - 2x - 2\left( {x - 2} \right)\;\;\left( 2 \right)\)
Hãy chọn đáp án đúng.
-
A.
Phương trình (1) vô nghiệm, phương trình (2) có nghiệm duy nhất
-
B.
Phương trình (1) có vô số nghiệm, phương trình (2) vô nghiệm
-
C.
Phương trình (1) vô nghiệm, phương trình (2) có vô số nghiệm
-
D.
Cả phương trình (1) và phương trình (2) đều có một nghiệm
Bài 6 :
Cho phương trình: \(\frac{{x - 11}}{{2011}} + \frac{{x - 10}}{{2012}} = \frac{{x - 74}}{{1948}} + \frac{{x - 72}}{{1950}}\).
Khẳng định nào sau đây đúng?
-
A.
Nghiệm của phương trình là một chia hết cho 5
-
B.
Nghiệm của phương trình là một số chia hết cho 2
-
C.
Nghiệm của phương trình là một chia hết cho 4
-
D.
Nghiệm của phương trình là một số nguyên tố
Bài 7 :
Tìm điều kiện của m để phương trình \(3mx + m - 4x = 3{m^2} + 1\) có nghiệm duy nhất
-
A.
\(m \ne \frac{4}{3}\)
-
B.
\(m = \frac{4}{3}\)
-
C.
\(m = \frac{3}{4}\)
-
D.
\(m \ne \frac{3}{4}\)
Bài 8 :
Hình tam giác và hình chữ nhật ở hình dưới có cùng chu vi. Khi đó, giá trị của x là:

-
A.
\(x = - 2\)
-
B.
\(x = 2\)
-
C.
\(x = 1\)
-
D.
\(x = - 1\)
Bài 9 :
Cho hai phương trình \(\frac{{7x}}{8} - 5\left( {x - 9} \right) = \frac{1}{6}\left( {20x + 1,5} \right)\left( 1 \right)\) và \(2\left( {a - 1} \right)x - a\left( {x - 1} \right) = 2a + 3\;\left( 2 \right)\)
Để phương trình (2) có một nghiệm bằng một phần ba nghiệm của phương trình (1) thì giá trị của a là:
-
A.
\(a = 7\)
-
B.
\(a = - 7\)
-
C.
\(a = \frac{1}{7}\)
-
D.
\(a = \frac{{ - 1}}{7}\)
Bài 10 :
Phương trình \(\frac{{x + 1}}{3} + \frac{{3\left( {2x + 1} \right)}}{4} = \frac{{2x + 3\left( {x + 1} \right)}}{6} + \frac{{7 + 12x}}{{12}}\) có bao nhiêu nghiệm?
-
A.
1 nghiệm
-
B.
2 nghiệm
-
C.
Không có nghiệm nào
-
D.
Có vô số nghiệm
Bài 11 :
Cho phương trình: \(\frac{{2 - x}}{{2001}} - 1 = \frac{{1 - x}}{{2002}} - \frac{x}{{2003}}\;\;\left( 1 \right)\)
Gọi \({x_0}\) là nghiệm của phương trình (1). Chọn đáp án đúng
-
A.
\({x_0} - 3 = 200\)
-
B.
\({x_0} - 3 = - 2000\)
-
C.
\({x_0} - 3 = 2000\)
-
D.
\({x_0} - 3 = - 200\)
Bài 12 :
Cho hình vẽ dưới đây. Biết rằng diện tích của cả hình đó bằng \(168{m^2}.\) Khi đó, giá trị của x (mét) là:
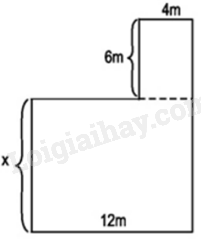
-
A.
11m
-
B.
12m
-
C.
13m
-
D.
14m
Bài 13 :
Một xe máy khởi hành từ Hà Nội đi Hải Phòng với vận tốc trung bình 32km/h. Sau đó 1 giờ, một ô tô cũng khởi hành từ Hà Nội đi Hải Phòng, cùng đường với xe máy và với vận tốc trung bình 48km/h. Phương trình biểu thị việc ô tô gặp xe máy sau x giờ, kể từ khi ô tô khởi hành là:
-
A.
\(48 = 32\left( {x - 1} \right)\)
-
B.
\(48x = 32\left( {1 - x} \right)\)
-
C.
\(48x = 32\left( {x - 1} \right)\)
-
D.
\(48x = 32\left( {x + 1} \right)\)
Bài 14 :
Cho phương trình \(\left( {{m^2} - 3m + 2} \right)x = m - 2,\) với m là tham số. Giá trị của m để phương trình có vô số nghiệm là:
-
A.
\(m = 1\)
-
B.
\(m = 2\)
-
C.
\(m \in \left\{ {1;2} \right\}\)
-
D.
\(m = 0\)
Bài 15 :
Giải các phương trình sau:
a) 5x−(2−4x)=6+3(x−1)
b) \(\frac{{x - 1}}{4}\)+2x=3 - \(\frac{{2{\rm{x}} - 3}}{3}\)
Bài 16 :
Hai bạn Lan và Hương cùng vào hiệu sách. Lan mua 5 quyển vở cùng loại và 1 quyển sách giá 50 nghìn đồng. Hương mua 3 quyển vở cùng loại với loại vở của Lan và 1 quyển sách giá 74 nghìn đồng. Số tiền phải trả của Lan và Hương là bằng nhau
a) Gọi x (nghìn đồng) là giá tiền của mỗi quyển vở. Viết phương trình biểu thị tổng số tiền mua sách và vở của hai bạn Lan và Hương là bằng nhau
b) Giải phương trình nhận được ở câu a để tìm giá tiền của mỗi quyển vở
Bài 17 :
Giải các phương trình sau:
a) 7x−(2x+3)=5(x−2)
b) x + \(\frac{{2{\rm{x}} - 1}}{5}\)=3 + \(\frac{{3 - x}}{4}\)
Bài 18 :
Hiện nay tuổi của bố bạn Nam gấp 3 lần tuổi của Nam. Sau 10 năm nữa thì tổng số tuổi của Nam và bố là 76 tuổi. Gọi x là số tuổi hiện nay của Nam
a) Biểu thị tuổi hiện nay của bố bạn Nam theo tuổi hiện tại của Nam
b) Viết phương trình biểu thị sự kiện sau 10 năm nữa thì tổng số tuổi của nam và bố là 76 tuổi
c) Giải phương trình nhận được ở câu b để tính tuổi của Nam và bố hiện nay
Bài 19 :
Bạn Mai mua cả sách và vở hết 500 nghìn đồng. Biết rằng số tiền mua sách nhiều gấp rưỡi số tiền mua vở, hãy tính số tiền bạn Mai dùng để mua mỗi loại
Bài 20 :
Giải các phương trình sau:
a) x−3(2−x)=2x−4
b) \(\frac{1}{2}\left( {x + 5} \right) - 4 = \frac{1}{3}\left( {x - 1} \right)\)
c) 3(x−2)−(x+1)=2x−4
d) 3x−4=2(x−1)−(2−x)
Bài 21 :
Bạn Nam giải phương trình x(x+1)=x(x+2) như sau:
x+1=x+2
x−x=2−1
0x=1 (vô nghiệm)
Em có đồng ý cách giải của bạn Nam không? Nếu không đồng ý, hãy trình bày cách giải của em.
Bài 22 :
Tập nghiệm S của phương trình 3(x+1)−(x−2)=7−2x là
A. S=0 B. S={\(\frac{1}{2}\)}
C.S=∅ D. S=R
Bài 23 :
Giải các phương trình sau:
a) 5(x−1)−(6−2x)=8x−3
b) \(\frac{{2{\rm{x}} - 1}}{3} - \frac{{5 - 3{\rm{x}}}}{2} = \frac{{x + 7}}{4}\)
Bài 24 :
Giải các phương trình sau:
a) \(15 - 4x = x - 5\);
b) \(\dfrac{{5x + 2}}{4} + \dfrac{{3x - 2}}{3} = \dfrac{3}{2}\).
Bài 25 :
Giải các phương trình sau:
a) \(5x - 30 = 0\);
b) \(4 - 3x = 11\);
c) \(3x + x + 20 = 0\);
d) \(\dfrac{1}{3}x + \dfrac{1}{2} = x + 2\).
Bài 26 :
Giải các phương trình sau:
a) \(8 - \left( {x - 15} \right) = 2.\left( {3 - 2x} \right)\);
b) \( - 6\left( {1,5 - 2u} \right) = 3\left( { - 15 + 2u} \right)\);
c) \({\left( {x + 3} \right)^2} - x\left( {x + 4} \right) = 13\);
d) \(\left( {y + 5} \right)\left( {y - 5} \right) - {\left( {y - 2} \right)^2} = -5\).
Bài 27 :
Giải phương trình: \(\dfrac{{5x - 3}}{4} = \dfrac{{x + 2}}{3}\);
Bài 28 :
Giải phương trình: \(\dfrac{{9x + 5}}{6} = 1 - \dfrac{{6 + 3x}}{8}\);
Bài 29 :
Giải phương trình: \(\dfrac{{2\left( {x + 1} \right)}}{3} - \dfrac{1}{2} = \dfrac{{1 + 3x}}{4}\);
Bài 30 :
Giải phương trình: \( \frac {x+3}{5} - \frac{2}{3}x = \frac{3}{10}\)












