Nội dung từ Loigiaihay.Com
Giá trị của tham số $m$ để đường tiệm cận đứng của đồ thị hàm số $y = \dfrac{{2x + 1}}{{x + m}}$ đi qua điểm $M\left( {2;3} \right)$ là
-
A.
\(3\)
-
B.
$ - 2$
-
C.
$2$
-
D.
$0$
Đồ thị hàm số có dạng $y = \dfrac{{ax + b}}{{cx + d}}$ có tiệm cận ngang $y = \dfrac{a}{c}$ và tiệm cận đứng $x = - \dfrac{d}{c}$
Đồ thị hàm số có tiệm cận đứng $x = - m{\mkern 1mu} {\mkern 1mu} \left( d \right),M \in d \Rightarrow 2 = - m \Rightarrow m = - 2.$
Đáp án : B

Các bài tập cùng chuyên đề
Bài 1 :
Đồ thị hàm số nào sau đây có 3 đường tiệm cận?
-
A.
\(y = \dfrac{{x + 2}}{{{x^2} + 3x + 6}}\)
-
B.
\(y = \dfrac{{x + 1}}{{{x^2} - 9}}\)
-
C.
\(y = \dfrac{{x + 2}}{{x - 1}}\)
-
D.
\(y = \dfrac{{x + 1}}{{\sqrt {{x^2} + 4x + 8} }}\)
Bài 2 :
Giao điểm của hai đường tiệm cận của đồ thị hàm số nào dưới đây nằm trên đường thẳng $d:y = x$?
-
A.
$y = \dfrac{{2x - 1}}{{x + 3}}$
-
B.
$y = \dfrac{{x + 4}}{{x - 1}}$
-
C.
$y = \dfrac{{2x + 1}}{{x + 2}}$
-
D.
$y = \dfrac{1}{{x + 3}}$
Bài 3 :
Trong các hàm số sau, đồ thị hàm số nào không có đường tiệm cận?
-
A.
$y = \dfrac{x}{{\sqrt {{x^2} + 2} }}$
-
B.
$y = \dfrac{1}{{{x^2} - 1}}$
-
C.
$y = \dfrac{{3x + 2}}{{4x - 3}}$
-
D.
$y = {x^4} - 2018$
Bài 4 :
Đồ thị hàm số nào sau đây có 3 đường tiệm cận?
-
A.
\(y = \dfrac{{2 - x}}{x}\).
-
B.
\(y = \dfrac{x}{{{x^2} - x + 1}}\).
-
C.
\(y = \dfrac{1}{{{x^2} - 1}}\).
-
D.
\(y = \dfrac{{x - 1}}{{x + 1}}\).
Bài 5 :
Tìm các tiệm cận ngang và tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right) = \frac{{2x + 1}}{{x - 4}}\).
Bài 6 :
Tìm các tiệm cận đứng và tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right) = \frac{{{x^2} - 4x + 2}}{{1 - x}}\).
Bài 7 :
Hình 1.26 là đồ thị của hàm số \(y = f\left( x \right) = \frac{{2{x^2}}}{{{x^2} - 1}}\)
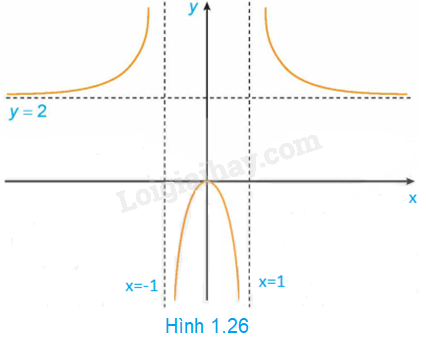
Sử dụng đồ thị này, hãy:
a) Viết kết quả của các giới hạn sau: \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right)\); \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\); \(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right)\); \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right)\)
b) Chỉ ra các tiệm cận của đồ thị hàm số đã cho.
Bài 8 :
Tìm các tiệm cận của đồ thị hàm số sau:
a) \(y = \frac{{3 - x}}{{2x + 1}}\);
b) \(y = \frac{{2{x^2} + x - 1}}{{x + 2}}\).
Bài 9 :
Một mảnh vườn hình chữ nhật có diện tích bằng \(144{m^2}\). Biết độ dài một cạnh của mảnh vườn là x (m).
a) Viết biểu thức tính chu vi P(x) (mét) của mảnh vườn.
b) Tìm các tiệm cận của đồ thị hàm số P(x).
Bài 10 :
Cho hàm số \(y = f\left( x \right)\) thỏa mãn: \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = 1;\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = 1;\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 2\) và \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2\). Khẳng định nào sau đây là đúng?
A. Đường thẳng \(x = 2\) là tiệm cận đứng của đồ thị hàm số.
B. Đường thẳng \(y = 2\) là tiệm cận ngang của đồ thị hàm số.
C. Đường thẳng \(y = 1\) là tiệm cận ngang của đồ thị hàm số.
D. Đường thẳng \(x = 2\) là tiệm cận ngang của đồ thị hàm số.
Bài 11 :
Cho hàm số \(y = f\left( x \right)\) xác định trên \[\mathbb{R}\backslash \left\{ {1;3} \right\}\], liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:

Khẳng định nào sau đây là sai?
A. Đường thẳng \(y = 1\) là tiệm cận ngang của đồ thị hàm số đã cho.
B. Đường thẳng \(y = - 1\) là tiệm cận ngang của đồ thị hàm số đã cho.
C. Đường thẳng \(x = 3\) là tiệm cận đứng của đồ thị hàm số đã cho.
D. Đường thẳng \(x = 1\) là tiệm cận đứng của đồ thị hàm số đã cho.
Bài 12 :
Đồ thị trong Hình 1.37 là đồ thị của hàm số:

A. \(y = \frac{{x + 2}}{{x + 1}}\).
B. \(y = \frac{{2x + 1}}{{x + 1}}\).
C. \(y = \frac{{x - 1}}{{x + 1}}\).
D. \(y = \frac{{x + 3}}{{1 - x}}\).
Bài 13 :
Đồ thị trong Hình 1.38 là đồ thị của hàm số:
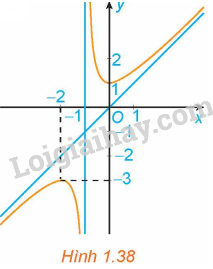
A. \(y = x - \frac{1}{{x + 1}}\).
B. \(y = \frac{{2x + 1}}{{x + 1}}\).
C. \(y = \frac{{{x^2} - x + 1}}{{x + 1}}\).
D. \(y = \frac{{{x^2} + x + 1}}{{x + 1}}\).
Bài 14 :
Tìm các tiệm cận của mỗi đồ thị hàm số sau:
a) \(y = \frac{{3x - 2}}{{x + 1}}\);
b) \(y = \frac{{{x^2} + 2x - 1}}{{2x - 1}}\).
Bài 15 :
Tổng số các đường tiệm cận của đồ thị hàm số \(y = \frac{{\sqrt {{x^2} - 1} }}{x}\) là
A. 0.
B. 1.
C. 2.
D. 3.
Bài 16 :
Tìm tiệm cận đứng, ngang, xiên (nếu có) của đồ thị mỗi hàm số sau:
a) \(y = \frac{x}{{2 - x}}\)
b) \(y = \frac{{2{x^2} - 3x + 2}}{{x - 1}}\)
c) \(y = x - 3 + \frac{1}{{{x^2}}}\)
Bài 17 :
Số đường TCĐ và TCN của hàm số \(y = \frac{{4x + 4}}{{{x^2} + 2x + 1}}\) là:
A. 0.
B.1.
C. 2.
D. 3.
Bài 18 :
Tìm các đường TCN và TCĐ của mỗi hàm số sau:
A. \(y = \frac{{5x + 1}}{{3x - 2}}\)
B. \(y = \frac{{2{x^3} - 3x}}{{{x^3} + 1}}\)
C. \(y = \frac{x}{{\sqrt {{x^2} - 4} }}\)
Bài 19 :
Tìm các đường tiệm cận đứng và tiệm cận xiên của đồ thị mỗi hàm số sau:
\(a,\;y = x - 3 + \frac{1}{{{x^2}}}\)
\(b,\;y = \frac{{2{x^2} - 3x + 2}}{{x - 1}}\)
\(\;c,y = \frac{{2{x^2} - x + 3}}{{2x + 1}}\)
Bài 20 :
Nếu trong một ngày, một xưởng sản xuất được x kilôgam sản phẩm thì chi phí trung bình (tính bằng nghìn đồng) cho một sản phẩm được cho bởi công thức: \(C(x) = \frac{{50x + 2000}}{x}\)
Tìm các đường tiệm cận của hàm số C(x).
Bài 21 :
Tìm các tiệm cận đứng và tiệm cận ngang của đồ thị hàm số sau:
a) \(y = \frac{{4x - 5}}{{2x - 3}}\)
b) \(y = \frac{{ - 2x + 7}}{{4x - 3}}\)
c) \(y = \frac{{5x}}{{3x - 7}}\)
Bài 22 :
Tìm các tiệm cận của đồ thị hàm số sau:
a) \(y = \frac{{2x - 3}}{{5{x^2} - 15x + 10}}\)
b) \(y = \frac{{{x^2} + x - 1}}{x}\)

c) \(y = \frac{{16{x^2} - 8x}}{{16{x^2} + 1}}\)
Bài 23 :
Tìm các tiệm cận đứng và tiệm cận xiên của đồ thị hàm số sau:
a) \(y = \frac{{{x^2} + 2}}{{2x - 3}}\)
b) \(y = \frac{{2{x^2} - 3x - 6}}{{x + 2}}\)
c) \(y = \frac{{2{x^2} + 9x + 11}}{{2x + 5}}\)
Bài 24 :
Tìm tiệm cận của đồ thị hàm số khối lượng hạt \(m(v) = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\) trong Khởi động: Theo thuyết tương đối hẹp, khối lượng m (kg) của một hạt phụ thuộc vào tốc độ di chuyển v (km/s) của nó trong hệ quy chiếu quán tính theo công thức \(m(v) = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\)trong đó \({m_0}\) là khối lượng nghỉ của hạt, c = 300 000 km/s là tốc độ ánh sáng.
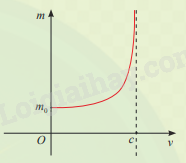
(Theo: https://www.britannica.com/science/relativistic-mass)
Bài 25 :
Cho hàm số f(x) có đồ thị như hình dưới đây:
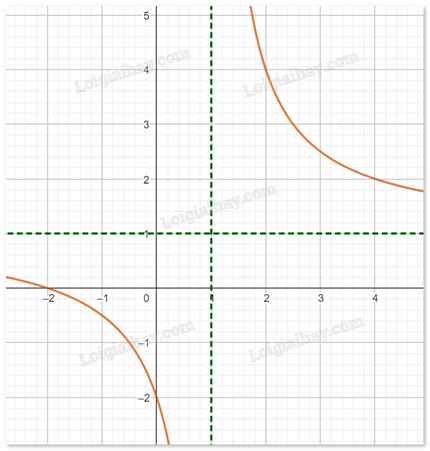
Phát biểu nào sau đây đúng?
-
A.
Đồ thị hàm số có tiệm cận đứng x = -1, tiệm cận ngang y = 1
-
B.
Đồ thị hàm số có tiệm cận đứng x = 1, tiệm cận ngang y = -1
-
C.
Đồ thị hàm số có tiệm cận đứng x = 1, tiệm cận ngang y = 1
-
D.
Đồ thị hàm số có tiệm cận đứng x = -1, tiệm cận ngang y = -1
Bài 26 :
Đồ thị hàm số dưới đây có bao nhiêu đường tiệm cận?
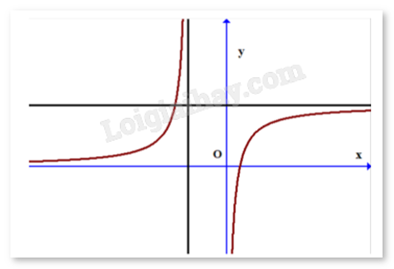
-
A.
0
-
B.
2
-
C.
1
-
D.
4
Bài 27 :
Cho hàm số y = f(x) có bảng biến thiên như sau:

Tổng số tiệm cận ngang và số tiệm cận đứng của đồ thị hàm số đã cho là:
-
A.
4
-
B.
1
-
C.
3
-
D.
2
Bài 28 :
Tìm điều kiện của tham số m để đồ thị của hàm số \(y = \frac{{(2m + 1)x + 3}}{{x + 1}}\) có đường tiệm cận đi qua điểm A(-2;7).
Bài 29 :
Tìm hai số a, b để đồ thị hàm số \(y = \frac{{(4a - b){x^2} + ax + 1}}{{{x^2} + ax + b - 12}}\) nhận trục hoành và trục tung làm hai tiệm cận. Tổng của a và b bằng bao nhiêu?
Bài 30 :
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận?
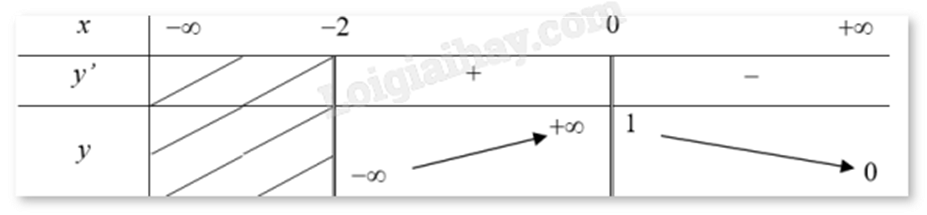
-
A.
1
-
B.
3
-
C.
2
-
D.
4












