Tính bán kính \(r\) của đường tròn nội tiếp tam giác đều cạnh \(a\).

Bài 1 :

Tam giác ABC có ba cạnh là 6, 8, 10. Khi đó, bán kính đường tròn nội tiếp tam giác ABC là

Bài 2 :

Tam giác \(ABC\) vuông tại \(A\) có \(AB = 6\)cm, \(BC = 10\)cm. Tính bán kính \(r\) của đường tròn nội tiếp tam giác đã cho.

Bài 3 :

Tam giác \(ABC\) có \(AB = 5,{\rm{ }}AC = 8\) và \(\widehat {BAC} = {60^0}\). Tính bán kính \(r\) của đường tròn nội tiếp tam giác đã cho.

Bài 4 :

Tam giác \(ABC\) có \(a = 21,{\rm{ }}b = 17,{\rm{ }}c = 10\). Tính bán kính \(r\) của đường tròn nội tiếp tam giác đã cho.

Bài 5 :

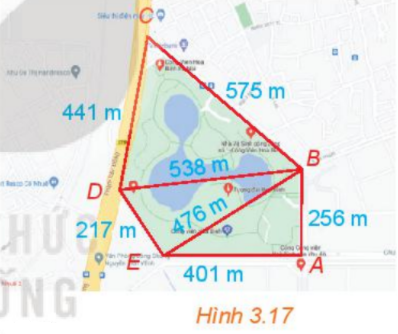
Công viên Hòa Bình (Hà Nội) có dạng hình ngũ giác ABCDE như hình 3.17. Dùng chế dộ tình khoảng cách giữa hai điểm của Google Maps, một người xác định được các khoảng cách như trong hình vẽ. Theo số liệu đó, em hãy tính diện tích của công viên hòa bình.

Bài 6 :

Ta đã biết tính cos A theo độ dài các cạnh của tam giác ABC. Liệu sin A và diện tích S có tính theo độ dài các cạnh của tam giác ABC hay không?

Bài 7 :

Tính diện tích tam giác ABC có \(b = 2,\;\widehat B = {30^o},\;\widehat C = {45^o}\).

Bài 8 :

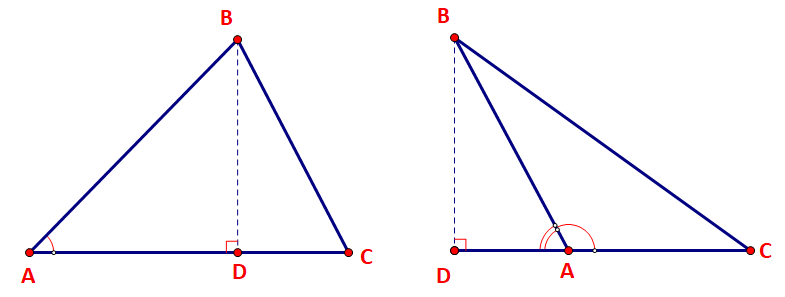
Cho tam giác ABC với đường cao BD.

a) Biểu thị BD theo AB và sinA.

b) Viết công thức tính diện tích S của tam giác ABC theo b,c, sin A.

Bài 9 :

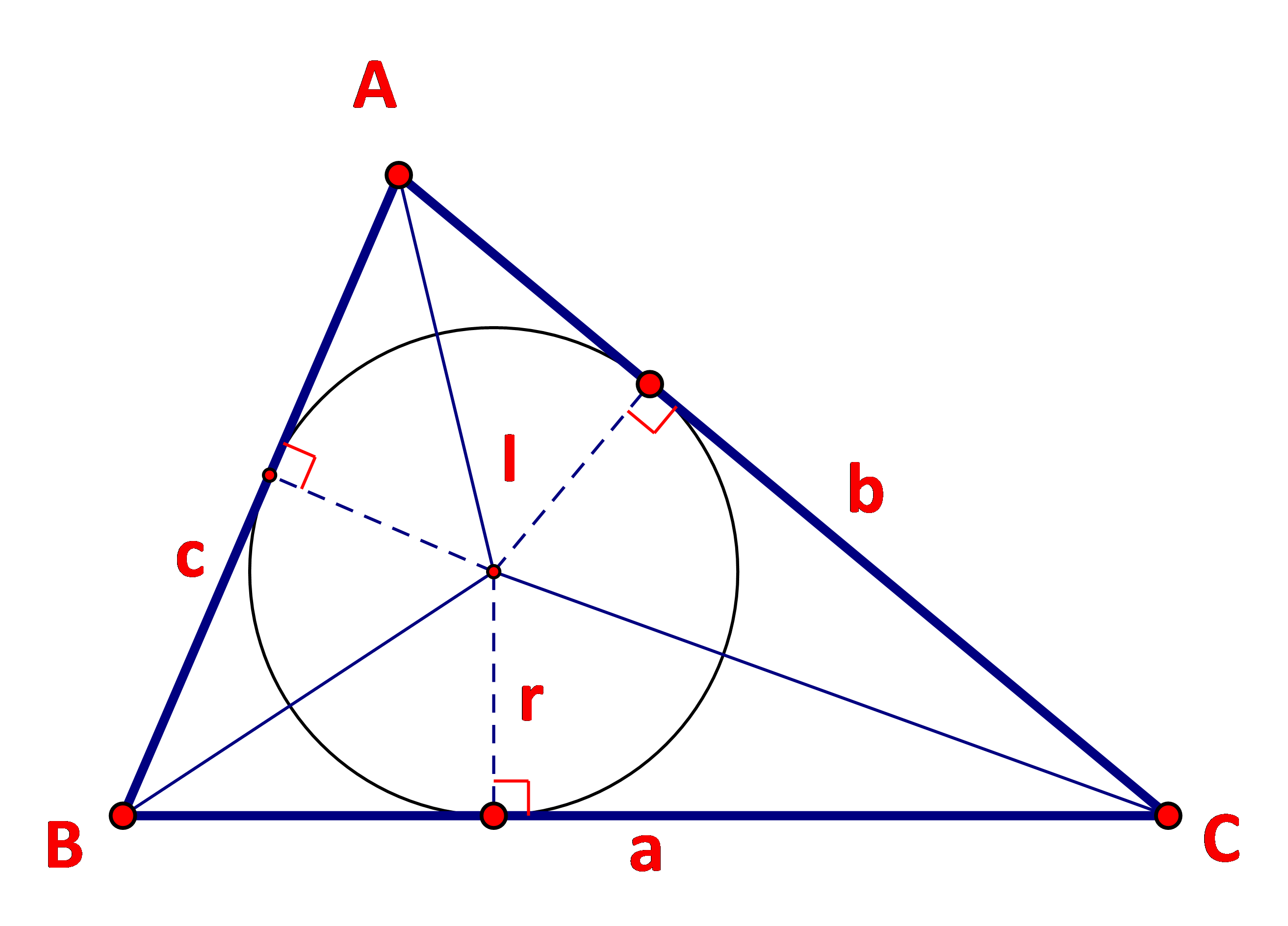
Cho tam giác ABC với I là tâm đường trong nội tiếp tam giác.

a) Nêu mối liên hệ giữa diện tích tam giác ABC và diện tích các tam giác IBC, ICA, IAB.

b) Tính diện tích tam giác ABC theo r,a,b,c.

Bài 10 :

A. \(S = \frac{1}{2}ca\)

B. \(S = \frac{{ - \sqrt 2 }}{4}ac\)

C. \(S = \frac{{\sqrt 2 }}{4}bc\)

D. \(S = \frac{{\sqrt 2 }}{4}ca\)

Bài 11 :

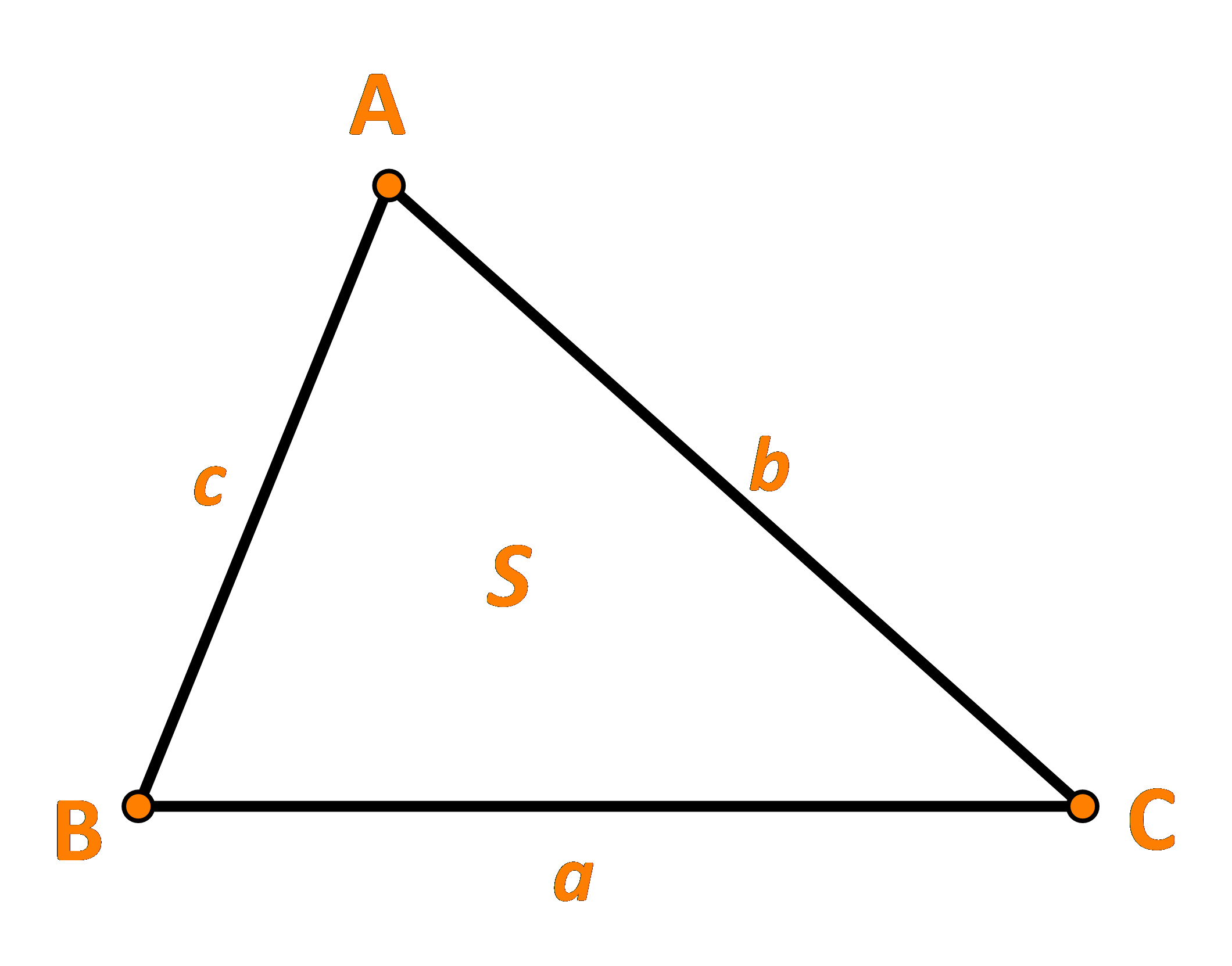
Cho tam giác ABC có BC = a, AC = b, AB =c và diện tích là S. (Hình 24).

a) Từ định lí cosin, chứng tỏ rằng:

\(\sin A = \frac{2}{{bc}}\sqrt {p(p - a)(p - b)(p - c)} \) ở đó \(p = \frac{{a + b + c}}{2}\)

b) Bằng cách sử dụng công thức \(S = \frac{1}{2}bc\sin A\),hãy chứng tỏ rằng: \(S = \sqrt {p(p - a)(p - b)(p - c)} \)

Bài 12 :

Cho tam giác ABC có AB = 12; \(\widehat B = {60^o}\); \(\widehat C = {45^o}\). Tính diện tích của tam giác ABC.

Bài 13 :

Tính diện tích một cánh buồm hình tam giác. Biết cách buồm đó có chiều dài một cạnh là 3,2 m và hai góc kề cách đó có số đo là \({48^o}\) và \({105^o}\) (Hình 12).

Bài 14 :

Tính diện tích tam giác ABC và bán kính đường tròn ngoại tiếp tam giác ABC trong các trường hợp sau:

a) Các cạnh \(b = 14,c = 35\) và \(\widehat A = {60^o}\)

b) Các cạnh \(a = 4,b = 5,c = 3\)

Bài 15 :

Cho tam giác ABC có BC = a, AC = b, AB = c và (I;r) là đường tròn nội tiếp tam giác (Hình 11).

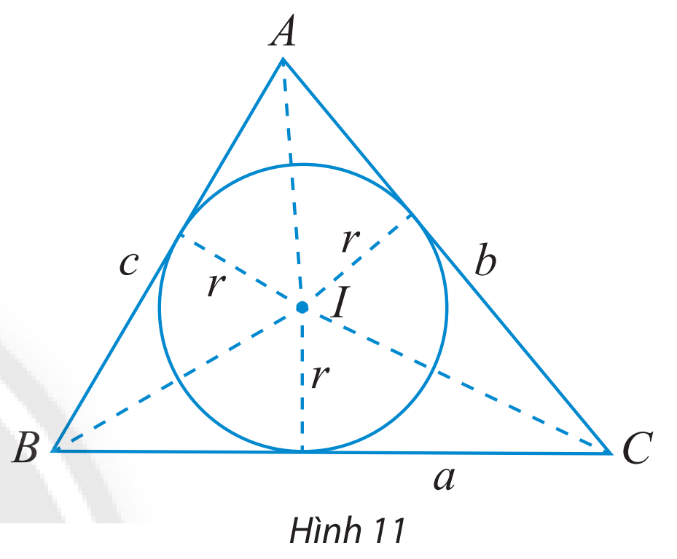
a) Tính diện tích các tam giác IBC, IAC, IAB theo r và a, b, c.

b) Dùng kết quả trên để chứng minh công thức tính diện tích tam giác ABC: \(S = \frac{{r(a + b + c)}}{2}\)

Bài 16 :

Cho tam giác ABC như Hình 10.

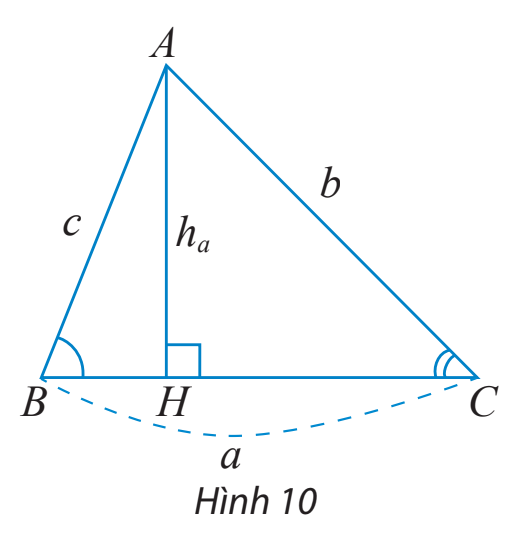
a) Viết công thức tính diện tích S của tam giác ABC theo a và \({h_a}\)

b) Tính \({h_a}\) theo b và sinC.

c) Dùng hai kết quả trên để chứng minh công thức \(S = \frac{1}{2}ab\sin C\)

d) Dùng định lí sin và kết quả ở câu c) để chứng minh công thức \(S = \frac{{abc}}{{4R}}\)

Bài 17 :

Tính diện tích một lá cờ hình tam giác cân có độ dài cạnh bên là 90 cm và góc ở đỉnh là \({35^o}.\)

Bài 18 :

b) Diện tích tam giác ABC

Bài 19 :

Tam giác ABC có AB = 4 cm, AC = 8 cm, \(\widehat {BAC} = {60^o}\). Tính diện tích tam giác ABC.

Bài 20 :

Tam giác ABC có AB = 4, BC = 7, \(\widehat B = {150^o}\). Tính diện tích tam giác ABC.

Bài 21 :

Tam giác ABC có AB = 6, AC = 9, \(\widehat A = {60^o}\). Tính diện tích tam giác ABC.

Bài 22 :

Một mảnh đất có dạng hình tứ giác như hình vẽ. Diện tích (làm tròn đến hàng đơn vị) mảnh đất đó là bao nhiêu?

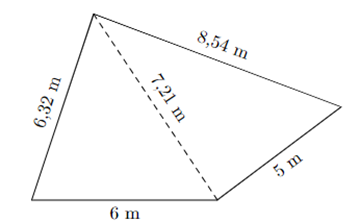
Bài 23 :

Tam giác \(ABC\) có \(a = 2,\,\,b = 3,\,\,c = 4.\) Bán kính đường tròn ngoại tiếp của tam giác \(ABC\) là:

A. \(R = \frac{{\sqrt {15} }}{2}.\)

B. \(R = \frac{7}{{\sqrt {15} }}.\)

C. \(R = \frac{{\sqrt {15} }}{6}.\)

D. \(R = \frac{8}{{\sqrt {15} }}.\)

Bài 24 :

Tam giác \(ABC\) có \(a = 4,\,\,b = 5,\,\,c = 6.\) Độ dài đường cao \({h_b}\) bằng:

A. \(\frac{{3\sqrt 7 }}{2}.\)

B. \(\frac{3}{{2\sqrt 7 }}.\)

C. \(\frac{{3\sqrt 7 }}{4}.\)

D. \(\frac{3}{{4\sqrt 7 }}.\)

Bài 25 :

Cho tam giác \(ABC\) có \(a = 20,\,\,b = 16\) và \({m_a} = 10.\) Diện tích của tam giác bằng:

A. \(92.\)

B. \(100.\)

C. \(96.\)

D. \(88.\)

Bài 26 :

Tam giác \(ABC\) có \(a = 14,\,\,b = 9\) và \({m_a} = 8.\) Độ dài đường cao \({h_a}\) bằng:

A. \(\frac{{24\sqrt 5 }}{7}.\)

B. \(\frac{{12\sqrt 5 }}{7}.\)

C. \(12\sqrt 5 .\)

D. \(24\sqrt 5 .\)

Bài 27 :

Cho tam giác ABC có \(a = 24\)cm, \(b = 26\)cm, \(c = 30\)cm

a) Tính diện tích tam giác ABC

b) Tính bán kính đường tròn nội tiếp của tam giác ABC

Bài 28 :

Cho tam giác MNP có \(MN = 10,MP = 20\) và \(\widehat M = 42^\circ \)

a) Tính diện tích tam giác MNP

b) Gọi O là tâm đường tròn ngoại tiếp tam giác MNP. Tính diện tích tam giác ONP

Bài 29 :

Cho tam giác ABC có trọng tâm G. Chứng minh các tam giác GBC, GAB, GAC có diện tích bằng nhau.

Bài 30 :

Cho tam giác ABC và có các điểm B’, C’ trên các cạnh AB, AC.

Chứng minh  \(\frac{{{S_{ABC}}}}{{{S_{AB'C'}}}} = \frac{{AB.AC}}{{AB'.AC'}}\).