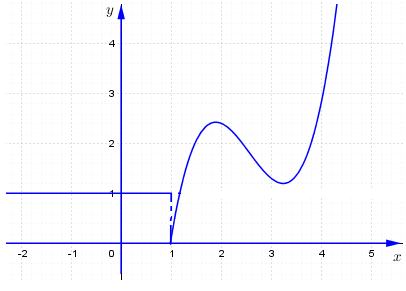
Cho đồ thị hàm số \(y = f\left( x \right)\) như hình vẽ. Mệnh đề nào sau đây sai?

Dựa vào đồ thị hàm số ta thấy \(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = 1,\,\,\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = 0 \Rightarrow \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) \Rightarrow \) Không tồn tại \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\), hàm số không liên tục tại $x = 1.$

Ngoài ra tại các điểm $x=0,x=2,x=3$ thì hàm số đều có đạo hàm.

Vậy hàm số không có đạo hàm tại $x = 1.$