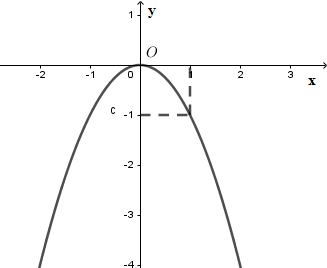
Hình vẽ dưới đây là của đồ thị hàm số nào?

Bài 1 :

Kết luận nào sau đây là sai khi nói về đồ thị của hàm số $y = a{x^2}\,\,$ với $a \ne 0$.

Bài 2 :

Cho hàm số $y = f\left( x \right) = \left( { - 2m + 1} \right){x^2}.$

Tìm giá trị của $m$ để đồ thị đi qua điểm $A\left( { - 2;4} \right).$

Bài 3 :

Cho hàm số $y = \left( {2m + 2} \right){x^2}$. Tìm $m$ để đồ thị hàm số đi qua điểm $A\left( {x;y} \right)$ với $\left( {x;y} \right)$ là nghiệm của hệ phương trình  $\left\{ \begin{array}{l}x - y = 1\\2x - y = 3\end{array} \right.$

Bài 4 :

Cho hàm số $y = \sqrt 3 {x^2}\,\,$có đồ thị là $(P)$.  Có bao nhiêu điểm trên $\left( P \right)$ có tung độ gấp đôi hoành độ.

Bài 5 :

Trong các điểm $A(1;2);B( - 1; - 1);C(10; - 200);D\left( {\sqrt {10} ; - 10} \right)$ có bao nhiêu điểm thuộc đồ thị hàm số $\left( P \right): y =  - {x^2}$

Bài 6 :

Cho $(P):y = \dfrac{1}{2}{x^2};(d):y = x - \dfrac{1}{2}$. Tìm toạ độ giao điểm của $(P)$ và $(d)$.

Bài 7 :

Cho parabol $y = \dfrac{1}{4}{x^2}$. Xác định $m$ để  điểm $A\left( {\sqrt 2 ;m} \right)$ nằm trên parabol.

Bài 8 :

Cho parabol$(P):y = 2{x^2}$ và đường thẳng $(d):y = x + 1$. Số giao điểm của đường thẳng $d$ và parabol $\left( P \right)$ là:

Bài 9 :

Cho parabol $(P):y = \left( {m - 1} \right){x^2}$ và đường thẳng $(d):y = 3 - 2x$. Tìm $m$ để đường thẳng $d$ cắt $\left( P \right)$ tại điểm có tung độ $y = 5$.

Bài 10 :

Cho parabol $(P):y = \left( {\dfrac{{1 - 2m}}{2}} \right){x^2}$ và đường thẳng $(d):y = 2x + 2$. Biết đường thẳng $d$ cắt $\left( P \right)$ tại một điểm có tung độ $y = 4$. Tìm hoành độ giao điểm còn lại của $d$ và parabol $\left( P \right)$.

Bài 11 :

Cho hàm số $y = f\left( x \right) = \dfrac{{2m - 3}}{3}{x^2}$ . Tìm giá trị của $m$ để đồ thị đi qua điểm $B\left( { - 3;5} \right)$

Bài 12 :

Cho hàm số $y = \left( { - 3m + 1} \right){x^2}$. Tìm $m$ để đồ thị hàm số đi qua điểm $A\left( {x;y} \right)$ với $\left( {x;y} \right)$ là nghiệm của hệ phương trình  $\left\{ \begin{array}{l}4x - 3y =  - 2\\x - 2y =  - 3\end{array} \right.$

Bài 13 :

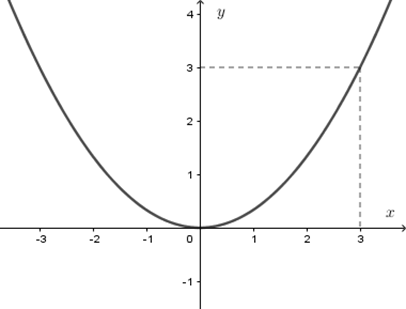
Hình vẽ dưới đây là của đồ thị hàm số nào?

Bài 14 :

Cho hàm số $y =  - \dfrac{2}{5}{x^2}\,\,$có đồ thị là $(P)$. Điểm trên $\left( P \right)$ (khác gốc tọa độ $O\left( {0;0} \right)$) có tung độ gấp ba lần hoành độ thì có hoành độ là:

Bài 15 :

Trong các điểm $A(5;5);B( - 5; - 5);C(10;20);D\left( {\sqrt {10} ;2} \right)$ có bao nhiêu điểm không thuộc đồ thị hàm số $y = \dfrac{1}{5}{x^2}\,\left( P \right)$

Bài 16 :

Cho $(P):y = 3{x^2};(d):y =  - 4x - 1$. Tìm toạ độ giao điểm của $(P)$ và $(d)$.

Bài 17 :

Cho parabol $y =  - \sqrt 5 {x^2}$. Xác định m để  điểm $A\left( {m\sqrt 5 ; - 2\sqrt 5 } \right)$ nằm trên parabol.

Bài 18 :

Cho parabol$(P):y = \sqrt {5m + 1} .{x^2}$ và đường thẳng $(d):y = 5x + 4$. Tìm $m$ để đường thẳng $d$ cắt $\left( P \right)$ tại điểm có tung độ $y = 9$.

Bài 19 :

Cho parabol$(P):y = \left( {\sqrt {3m + 4}  - \dfrac{7}{4}} \right){x^2}$ và đường thẳng $(d):y = 3x - 5$. Biết đường thẳng $d$ cắt $\left( P \right)$ tại một điểm có tung độ $y = 1$. Tìm $m$ và  hoành độ giao điểm còn lại của $d$ và parabol $\left( P \right)$.

Bài 20 :

Cho parabol$(P):y = 5{x^2}$ và đường thẳng $(d):y =  - 4x - 4$. Số giao điểm của đường thẳng $d$ và parabol $\left( P \right)$ là:

Bài 21 :

Xác định hàm số $y = a{x^2}$ biết rằng đồ thị của hàm số đi qua điểm $A\left( { - 2;5} \right)$.

Bài 22 :

Biết đồ thị hàm số $y = a{x^2}$ đi qua điểm $A\left( { - 1; - 2} \right),$ giá trị của $a$ bằng:

Bài 23 :

Tìm tọa độ giao điểm của đồ thị hai hàm số $y =  - {x^2}$ và $y = x - 2$

Bài 24 :

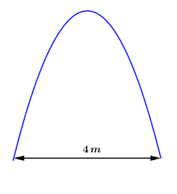
Cổng vào một ngôi biệt thự có hình dạng là một parabol được biểu diễn bởi đồ thị hàm số $y =  - {x^2}.$ Biết khoảng cách giữa hai chân cổng là $4\,m.$ Một chiếc ô tô tải có thùng xe là một hình hộp chữ nhật có chiều rộng là $2,4\,m.$ Hỏi chiều cao lớn nhất có thể của ô tô là bao nhiêu để ô tô có thể đi qua cổng? 

Bài 25 :

Đồ thị hàm số $y = \dfrac{1}{4}{x^2}$  đi qua điểm

Bài 26 :

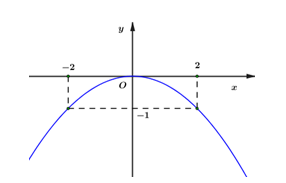
Cho hàm số $y = a{x^2}$ có đồ thị như hình vẽ bên. Hàm số đó là:

Bài 27 :

Đồ thị trong hình bên là của hàm số:

Bài 28 :

Tìm $m$ để đồ thị hàm số $y = \left( {m + 5} \right){x^2}$ đi qua điểm $A\left( { - 1;\,\,2} \right).$ 

Bài 29 :

Tìm $m$ để đồ thị hàm số $y = \left( {2m + 1} \right){x^2}$ đi qua điểm $A\left( {1;5} \right)$.

Bài 30 :

Cho hàm số $y=(2-\sqrt{m-1}){{x}^{2}}$. Tìm $m$ để đồ thị hàm số đi qua điểm $\left( 2;2 \right)$