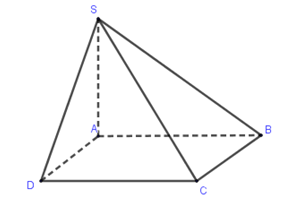
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, $SA \bot \left( {ABCD} \right)$, $SA = a\sqrt 6$. Gọi $\alpha$ là góc giữa $SC$ và $mp\left( {SAB} \right)$. Chọn khẳng định đúng trong các khẳng định sau?

Bước 1:

Do $BC \bot \left( {SAB} \right)$

$\Rightarrow$ B là hình chiếu của C lên $(SAB)$

Mà S là hình chiếu của chính nó lên $(SAB)$.

$\Rightarrow$ $SB$ là hình chiếu của $SC$ lên $\left( {SAB} \right)$

$\Rightarrow$ Góc giữa $SC$ và $(SAB)$ là góc giữa $SC$ và $SB$ và bằng $\widehat {BSC}$

Bước 2:

Ta có:

$SB = \sqrt {S{A^2} + A{B^2}} = \sqrt {6{a^2} + {a^2}} = a\sqrt 7$

Xét tam giác $SBC$ có

$\tan \widehat {BSC} = \dfrac{{BC}}{{SB}} = \dfrac{a}{{a\sqrt 7 }} = \dfrac{1}{{\sqrt 7 }}.$