Cho hình chóp \(S.ABDC\), với đáy \(ABCD\) là hình bình hành tâm \(O;AD,SA,AB\) đôi một vuông góc \(AD = 8,SA = 6\). \((P)\) là mặt phẳng qua trung điểm của \(AB\) và vuông góc với \(AB\). Thiết diện của \((P)\) và hình chóp có diện tích bằng?

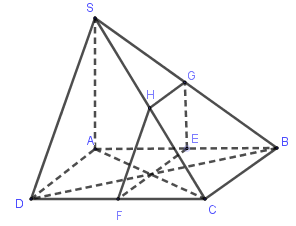
Gọi \(E\) là trung điểm của \(AB\).

Qua \(E\) kẻ \(EF \bot CD,EG \bot AB \Rightarrow \left( {EGF} \right) \bot AB\) và \(F,G\) là trung điểm của \(DC,SB\).

Do \(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\\left( {EGF} \right) \cap \left( {ABCD} \right) = FE\\FE//BC\end{array} \right. \) \(\Rightarrow \left( {SBC} \right) \cap \left( {EGF} \right) = GH//BC\) (định lý giao tuyến ba mặt phẳng).

Suy ra \(H\) là trung điểm của \(SC\).

Vậy thiết diện là hình thang \(GHFE\).

Vì \(GE//SA\) nên \(GE \bot \left( {ABCD} \right) \Rightarrow GE \bot FE\) nên thiết diện là hình thang vuông.

Vì ABCD là hình bình hành nên AD = BC = 8.

\({S_{EGHF}} = \dfrac{{\left( {FE + GH} \right).GE}}{2} \) \(= \dfrac{{\left( {BC + \dfrac{1}{2}BC} \right).\dfrac{1}{2}SA}}{2} \) \( = \dfrac{{\left( {8 + 4} \right)3}}{2} = 18\).