Nội dung từ Loigiaihay.Com
Đề bài
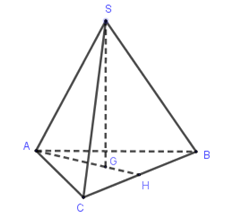
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\) và \(SA = SB = SC = b\). Gọi \(G\) là trọng tâm \(\Delta ABC\). Độ dài \(SG\) là:
-
A.
$\dfrac{{\sqrt {9{b^2} + 3{a^2}} }}{3}$.
-
B.
$\dfrac{{\sqrt {{b^2} - 3{a^2}} }}{3}$.
-
C.
$\dfrac{{\sqrt {9{b^2} - 3{a^2}} }}{3}$.
-
D.
$\dfrac{{\sqrt {{b^2} + 3{a^2}} }}{3}$.
Phương pháp giải
- Sử dụng tính chất hình chóp đều: Hình chiếu của đỉnh lên mặt đáy là trọng tâm của tam giác đáy.
- Từ đó tính được độ dài \(SG\) dựa vào mối quan hệ giữa cạnh và góc trong tam giác vuông.
Lời giải của GV HocTot.XYZ
Theo bài ra hình chóp \(S.ABC\) là hình chóp tam giác đều.
Gọi \(H\) là trung điểm của \(BC\), ta có \(SG \bot (ABC),G \in AH\).
Mà \(AH = \dfrac{{a\sqrt 3 }}{2} \Rightarrow AG = \dfrac{2}{3}AH = \dfrac{{a\sqrt 3 }}{3}\).
Tam giác \(SAG\) vuông tại \(G\) nên theo định lý Pi-ta-go ta có :
\(SG = \sqrt {S{A^2} - A{G^2}} = \sqrt {{b^2} - \dfrac{{{a^2}}}{3}} = \sqrt {\dfrac{{3{b^2} - {a^2}}}{3}} = \dfrac{{\sqrt {9{b^2} - 3{a^2}} }}{3}\)
Đáp án : C
Các bài tập cùng chuyên đề