Nội dung từ Loigiaihay.Com
Đề bài
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông. Mặt bên \(SAB\) là tam giác đều có đường cao \(SH\) vuông góc với \(mp(ABCD)\). Gọi \(\alpha \) là góc giữa \(BD\) và \(mp(SAD)\). Chọn khẳng định đúng trong các khẳng định sau?
-
A.
\(\alpha = {60^0}\).
-
B.
\(\alpha = {30^0}\).
-
C.
\(\cos \alpha = \dfrac{{\sqrt 3 }}{{2\sqrt 2 }}\).
-
D.
\(\sin \alpha = \dfrac{{\sqrt 3 }}{{2\sqrt 2 }}\).
Phương pháp giải
- Gọi \(I\) là trung điểm của \(BD\) và chứng minh \(BI \bot \left( {SAD} \right)\).
- Sử dụng định nghĩa góc giữa đường thẳng và mặt phẳng (không vuông) là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.
- Tính gia trị lượng giác của góc đó dựa vào tính chất tam giác vuông.
Lời giải của GV HocTot.XYZ
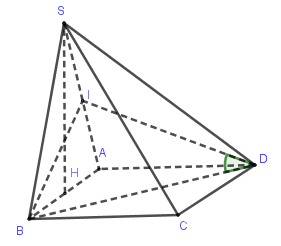
Gọi \(I\) là trung điểm ${\rm{AS}} \Rightarrow {\rm{BI}} \bot {\rm{SA}}$
Ta có: \(SH \bot \left( {ABCD} \right) \Rightarrow SH \bot AD\)
Mà \(AD \bot AB\) nên \(AD \bot \left( {SAB} \right) \Rightarrow AD \bot BI\)
Suy ra \(BI \bot (SAD) \Rightarrow \alpha = \widehat {IDB}\)
Ta có: \(BI = \dfrac{{AB\sqrt 3 }}{2},BD = AB\sqrt 2 \Rightarrow \sin \alpha = \dfrac{{BI}}{{BD}} = \dfrac{{\sqrt 3 }}{{2\sqrt 2 }}\)
Đáp án : D
Chú ý
Một số em có thể sẽ xác định nhầm góc \(\alpha \) là góc \(\widehat {IBD}\) là sai.
Các bài tập cùng chuyên đề