Nội dung từ Loigiaihay.Com
Cho đường tròn $\left( {O;R} \right)$, dây cung $AB = R\sqrt 3 $. Vẽ đường kính $CD \bot AB$ ($C$ thuộc cung lớn $AB$). Trên cung $AC$ nhỏ lấy điểm $M$, vẽ dây $AN{\rm{//}}CM$. Độ dài đoạn $MN$ là
-
A.
$MN = R\sqrt 3 $
-
B.
$MN = R\sqrt 2 $
-
C.
$MN = \dfrac{{3R}}{2}$
-
D.
$MN = \dfrac{{R\sqrt 5 }}{2}$
Sử dụng tính chất hai cung bị chắn giữa hai dây song song thì bằng nhau
Sử dụng mối liên hệ giữa dây và đường kính
Sử dụng định lý Pytago
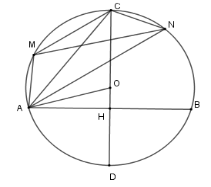
Vì hai dây $MC{\rm{//}}AN$ nên hai cung $AM$ và cung $CN$ bằng nhau, hay $AM = CN$
Suy ra $MCNA$ là hình thang cân $ \Rightarrow MN = AC$.
Gọi $H$ là giao của $CD$ và $AB$. Khi đó vì $AB \bot CD$ tại $H$ nên $H$ là trung điểm của $AB \Rightarrow AH = \dfrac{{AB}}{2} = \dfrac{{R\sqrt 3 }}{2}$
Xét tam giác vuông $AHO$, theo định lý Pytago ta có $OH = \sqrt {A{O^2} - A{H^2}} = \dfrac{R}{2}$$ \Rightarrow CH = \dfrac{{3R}}{2}$
Theo định lý Pytago cho tam giác $ACH$ vuông ta có $AC = \sqrt {C{H^2} + A{H^2}} = R\sqrt 3 $
Vậy $MN = R\sqrt 3 $.
Đáp án : A

Các bài tập cùng chuyên đề
Cho đường tròn $\left( O \right)$ có hai dây $AB,CD$ song song với nhau. Kết luận nào sau đây là đúng?
Chọn khẳng định đúng. Cho đường tròn $\left( O \right)$ có dây $AB > CD$ khi đó
Cho đường tròn $\left( O \right)$ có hai dây $AB,CD$ song song với nhau. Kết luận nào sau đây là đúng?
Cho đường tròn $(O)$ đường kính $AB$ và một cung $AC$ có số đo nhỏ hơn $90^\circ $. Vẽ dây $CD$ vuông góc với $AB$ và dây $DE$ song song với $AB$. Chọn kết luận sai?
Chọn khẳng định đúng.
Cho tam giác $ABC$ cân tại $A$ và $\widehat A = 66^\circ $ nội tiếp đường tròn $\left( O \right)$. Trong các cung nhỏ $AB;BC;AC$, cung nào là cung lớn nhất?
Cho đường tròn $\left( {O;R} \right)$ và hai dây $AB;CD$ sao cho $\widehat {AOB} = 120^\circ ;\widehat {COD} = 60^\circ $. So sánh các dây $CD;AB$.
Cho tam giác $ABC$ có $\widehat B = 60^\circ $, đường trung tuyến $AM$, đường cao $CH$. Vẽ đường tròn ngoại tiếp $BHM$. Kết luận nào đúng khi nói về các cung $HB;MB;MH$ của đường tròn ngoại tiếp tam giác $MHB$ ?
Cho đường tròn $(O;R)$ có hai dây cung $AB$ và $CD$ vuông góc với nhau tại $I$ ( $C$ thuộc cung nhỏ $AB$ ). Kẻ đường kính $BE$ của $(O)$. Đẳng thức nào sau đây là đúng?












