Nội dung từ Loigiaihay.Com
Chu vi đường tròn ngoại tiếp tam giác đều cạnh \(a\,\left( {cm} \right)\) là
-
A.
$\dfrac{{4\pi a\sqrt 3 }}{3} (cm)$
-
B.
$\dfrac{{2\pi a\sqrt 3 }}{3} (cm)$
-
C.
$\dfrac{{\pi a\sqrt 3 }}{3} (cm)$
-
D.
$\dfrac{{5\pi a\sqrt 3 }}{3}(cm)$
Sử dụng công thức chu vi đường tròn bán kính \(R\) là \(C = 2\pi R\,\)
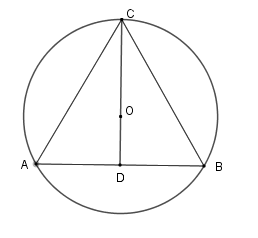
Gọi $O$ là tâm đường tròn ngoại tiếp tam giác đều \(BAC\) , suy ra \(O\) cũng là trọng tâm của tam giác \(ABC\) .
Tia \(CO \bot AB\) tại \(D\) thì $D$ là trung điểm của \(AB\) \( \Rightarrow OC = \dfrac{2}{3}CD\)
Xét tam giác vuông \(ADC\) có \(AC = a\,;\,\widehat {CAD} = 60^\circ \Rightarrow CD = AC.\sin 60^\circ = \dfrac{{a\sqrt 3 }}{2}\) \( \Rightarrow OC = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\)
Nên bán kính đường tròn ngoại tiếp tam giác \(ABC\) là \(R = \dfrac{{a\sqrt 3 }}{3} \Rightarrow C = 2\pi R = \dfrac{{2\pi a\sqrt 3 }}{3}\) .
Đáp án : B

Các bài tập cùng chuyên đề
Chu vi đường tròn bán kính \(R = 9\) là
Biêt chu vi đường tròn là \(C = 36\pi (cm)\). Tính đường kính của đường tròn.
Tính độ dài cung \(30^\circ \) của một đường tròn có bán kính \(4\,dm\)
Số đo \(n^\circ \) của cung tròn có độ dài \(30,8\,cm\) trên đường tròn có bán kính \(22\,cm\) là ( lấy \(\pi \approx 3,14\) và làm tròn đến độ)
Cho ba điểm $A,B,C$ thẳng hàng sao cho $B$ nằm giữa $A$ và $C$ . Chọn khẳng định nào sau đây đúng?
Cho tam giác $ABC$ vuông tại $A$ , cạnh $AB = 5\,\,cm$ , \(\widehat B = {60^ \circ }\). Đường tròn tâm $I$ , đường kính $AB$ cắt $BC$ ở $D$ . Chọn khẳng định sai?
Cho tam giác $ABC$ có \(AB = AC = 3\,\,cm,\,\,\widehat {\rm{A}} = {120^o}.\)Tính độ dài đường tròn ngoại tiếp tam giác $ABC$ .
Cho đường tròn $\left( O \right)$ bán kính $OA$ . Từ trung điểm $M$ của $OA$ vẽ dây\(BC \bot OA.\) Biết độ dài đường tròn $\left( O \right)$ là \(4\pi \,(cm).\) Độ dài cung lớn \(BC\) là












