Báo cáo thực hành: Khảo sát chuyển động rơi tự do. Xác định gia tốc rơi tự do1. Trả lời câu hỏi: Sự rơi tự do là gì ? Nếu đặc điểm của chuyển động rơi tự do và viết công thức tính gia tốc rơi tự do ?... Đề bài BÁO CÁO THỰC HÀNH: Khảo sát chuyển động rơi tự do. Xác định gia tốc rơi tự do Lời giải chi tiết 1. Trả lời câu hỏi: Sự rơi tự do là gì ? Nếu đặc điểm của chuyển động rơi tự do và viết công thức tính gia tốc rơi tự do ? - Sự rơi tự do là sự rơi chỉ dưới tác dụng của trọng lực. - Đặc điểm: + Phương thẳng đứng, chiều từ trên xuống. + Là chuyển động nhanh dần đều. + Tại một nơi nhất định trên Trái Đất và ở gần mặt đất, mọi vật đều rơi tự do với cùng gia tốc g. - Công thức tính gia tốc rơi tự do: \(g=\dfrac{2s}{t}\) Trong đó: + s : quãng đường đi được của vật rơi tự do (m). + t : thời gian vật rơi tự do (s). 2. Kết quả Bảng 8.1 Khảo sát chuyển động rơi tự do : Đo thời gian rơi ứng với các khoảng cách s khác nhau. Vị trí đầu của vật rơi: \(s_0 = 0 (mm)\).
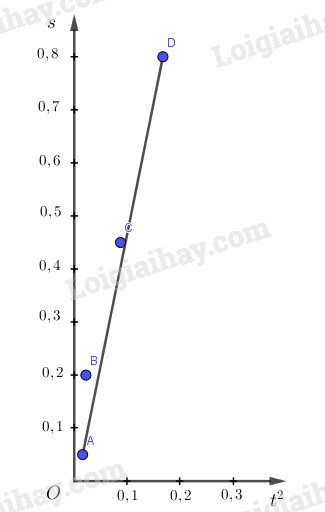
Trong đó: \(\overline {{t_i}} = \dfrac{{{t_1} + {t_2} + .. + {t_5}}}{5}\) Vẽ đồ thị: Dựa vào kết quả trong Bảng 8.1, chọn tỉ lệ thích hợp trên các trục tung và trục hoành để vẽ đồ thị \(s = s(t^2)\).
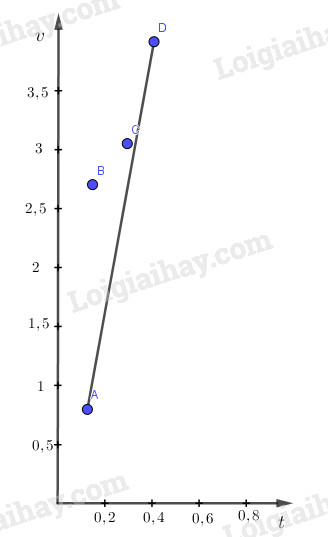
a) Nhật xét: Ta có: \(s = \dfrac{gt^2}{2} = s(t)\). Như vậy s phụ thuộc vào thời gian là hàm bậc 2 ẩn t, do vậy nếu vẽ đồ thị biểu diễn s qua t thì nó có dạng một đường cong Parabol. Nhưng bài toán hỏi dạng đồ thị của s theo ẩn \((t^2)\), do vậy chúng ta phải chú ý. Từ \(s =\dfrac{gt^2}{2} \to s = \dfrac{g.X}{2}\) với \(X = t^2\), ở đây t là biến nên X cũng là biến. Ta nhận thấy sự phụ thuộc của s theo ẩn X là một hàm số bậc nhất: \(Y = A.X + B\) (với \(A = g/2, B = 0\)) nên đồ thị \(s = s(t^2) = s(X)\) có dạng là một đường thẳng. Như vậy chuyển động của vật rơi tự do là chuyển động thẳng nhanh dần đều. b) Khi đã xác định được chuyển động rơi tự do là một chuyển động nhanh dần đều, ta có thể xác định các giá trị của g theo công thức \(g=\dfrac{2s}{t^2}\) và vận tốc của vật rơi tại cổng E theo công thức \(v=\dfrac{2s}{t}\) ứng với mỗi lần đo. Hãy tính các giá trị trên và ghi vào bảng 8.1 c) Đồ thị \(v = v(t)\) có dạng một đường thẳng, tức là vận tốc rơi tự do tăng dần theo thời gian. Vậy chuyển động rơi tự do là chuyển động thẳng nhanh dần đều
d) Ta có: \(\begin{array}{l}\overline g = \dfrac{{{g_1} + {g_2} + {g_3} + {g_4}}}{4}\\ = \dfrac{{6,339 + 18,261 + 10,342 + 9,583}}{4} \\= 11,13m/{s^2}\end{array}\) \(\begin{array}{l}\Delta {g_1} = \left| {\overline g - {g_1}} \right| = 4,791\\\Delta {g_2} = \left| {\overline g - {g_2}} \right| = 7,131\\\Delta {g_3} = \left| {\overline g - {g_3}} \right| = 0,788\\\Delta {g_4} = \left| {\overline g - {g_4}} \right| = 1,547\end{array}\) e) Kết quả: \(g = \overline g \pm {\left( {\Delta g} \right)_{max}} = 11,13 \pm 7,131\left( {m/{s^2}} \right)\) HocTot.XYZ
|