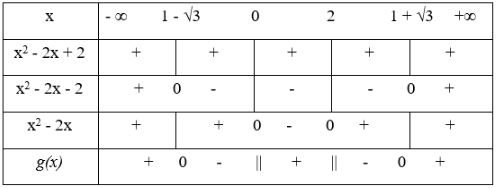
Bài 11 trang 107 SGK Đại số 10Hãy tìm nghiệm nguyên của bất phương trình sau: x(x3 – x + 6) > 9 Video hướng dẫn giải LG a Bằng cách sử dụng hằng đẳng thức \(a^2-b^2= (a-b)(a+b),\) hãy xét dấu \(f(x)= x^4– x^2+6x – 9\) và \(g(x) = x^2– 2x - {4 \over {{x^2} - 2x}}.\) Lời giải chi tiết: Ta có: f(x) = x4 – x2 + 6x – 9 = x4 – (x2 – 6x +9) = x4– (x-3)2 = (x2 –x + 3).(x2 + x - 3) + Tam thức x2 – x + 3 có Δ = -11 < 0, a = 1 > 0 nên x2 – x + 3 > 0 với ∀ x ∈ R. + Tam thức x2 + x – 3 có hai nghiệm \({x_1} = \dfrac{{ - 1 - \sqrt {13} }}{2},{x_2} = \dfrac{{ - 1 + \sqrt {13} }}{2}\) Ta có bảng xét dấu: Suy ra: +) \(f\left( x \right) > 0\) khi \(x < \dfrac{{ - 1 - \sqrt {13} }}{2}\) hoặc \(x > \dfrac{{ - 1 + \sqrt {13} }}{2}\) +) \(f\left( x \right) < 0\) khi \(\dfrac{{ - 1 - \sqrt {13} }}{2} < x < \dfrac{{ - 1 + \sqrt {13} }}{2}\) \(g(x) = x^2– 2x - {4 \over {{x^2} - 2x}}\) \(={{{{({x^2} - 2x)}^2} - {2^2}} \over {{x^2} - 2x}} = {{({x^2} - 2x + 2)({x^2} - 2x - 2)} \over {{x^2} - 2x}}\) Tam thức x2 - 2x + 2 có Δ = -4 < 0, hệ số a = 1 > 0 nên x2 - 2x + 2 > 0 với ∀ x ∈ R Tam thức x2 - 2x - 2 có hai nghiệm là x1 = 1 - √3; x2 = 1 + √3. Tam thức x2 - 2x có hai nghiệm là x1 = 0; x2 = 2 Lập bảng xét dấu: Vậy \(g\left( x \right) < 0 \Leftrightarrow x \in \left( {1 - \sqrt 3 };0 \right)\)\( \cup \left( {2;\;1 + \sqrt 3 } \right)\) và \(g\left( x \right) > 0 \Leftrightarrow x \in \left( { - \infty ;1 - \sqrt 3 } \right)\)\( \cup \left( {0;\;2} \right) \cup \left( {1 + \sqrt 3 ; + \infty } \right).\) LG b Hãy tìm nghiệm nguyên của bất phương trình sau: \(x(x^3– x + 6) > 9.\) Lời giải chi tiết: \(\eqalign{ & x({x^3} - x + 6) > 9 \cr&\Leftrightarrow {x^4} - {x^2} + 6x - 9 > 0 \cr & \Leftrightarrow f(x)>0 (1) \cr} \) Theo câu a, \(f\left( x \right) > 0 \Leftrightarrow \left[ \begin{array}{l} Mà \(x\in Z\) nên tập hợp nghiệm nguyên của bất phương trình là \(\left\{x\in \mathbb Z|x\le-3\text{ hoặc } x\ge2\right\}.\) HocTot.XYZ
|