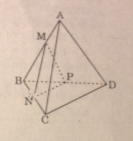
Câu 11 trang 80 SGK Hình học 11 Nâng caoCho tứ diện đều ABCD có cạnh bằng a, điểm M trên cạnh AB sao cho AM = m (0 < m < a). Khi đó, diện tích thiết diện của hình tứ diện khi cắt bởi mặt phẳng qua M và song song với mp(ACD) là: Đề bài Cho tứ diện đều ABCD có cạnh bằng a, điểm M trên cạnh AB sao cho AM = m (0 < m < a). Khi đó, diện tích thiết diện của hình tứ diện khi cắt bởi mặt phẳng qua M và song song với mp(ACD) là: A. m2√34 B. (a−m)2√22 C. (a+m)24 D. (a−m)2√34 Lời giải chi tiết
Vẽ MN // AC (N ϵ BC) MP // AD (P ϵ BD) Thiết diện cần tìm là ΔMNP Ta có: ΔMNP∽ΔACD tỉ số MPAD=BMAB=a−ma ⇒SMNPSACD=(MPAD)2=(a−ma)2 ⇒SMNP=(a−ma)2.SABC =(a−ma)2.a2√34=(a−m)2√34 Chọn (D) HocTot.XYZ  Chia sẻ Bình luận
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
|
