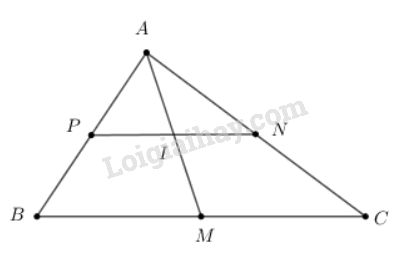
Bài 27 trang 32 SGK Hình học 10Các điểm M(2, 3); N(0, -4); P(-1, 6) lần lượt là trung điểm các cạnh BC, CA, AB của tam giác ABC. Tọa độ của đỉnh A là: Đề bài Các điểm \(M(2; 3); N(0; -4); P(-1; 6)\) lần lượt là trung điểm các cạnh \(BC, CA, AB\) của tam giác \(ABC\). Tọa độ của đỉnh \(A\) là: a) \((1; 5)\) b) \((-3; -1)\) c) \((-2; -7)\) d) \((1; -10)\) Video hướng dẫn giải Lời giải chi tiết
Cách 1: M, N là trung điểm BC, CA nên MN là đường trung bình của tam giác. \( \Rightarrow MN= \frac{1}{2}AB\) và \(MN//AB\) \( \Rightarrow MN//AP\) Mà \(AP = \frac{1}{2}AB \Rightarrow AP = MN\). Do đó \(APMN\) là hình bình hành \( \Rightarrow \overrightarrow {AP} = \overrightarrow {NM} \) \(\Leftrightarrow \left\{ \begin{array}{l} Cách 2: Trung tuyến \(AM\) cắt \(PN\) tại \(I\) thì \(I\) là trung điểm của \(PN\) nên \(I( - {1 \over 2}; 1)\) và \(I\) cũng là trung điểm của \(AM\). \(\Rightarrow \left\{ \matrix{ \(\Leftrightarrow \left\{ \matrix{ Vậy \(A(-3, -1) ⇒\) chọn B. Cách 3: M là trung điểm BC nên ta có: \(\left\{ \begin{array}{l}{x_B} + {x_C} = 2{x_M} = 4\\{y_B} + {y_C} = 2{y_M} = 6\end{array} \right.\) N là trung điểm CA nên ta có: \(\left\{ \begin{array}{l}{x_C} + {x_A} = 2{x_N} = 0\\{y_C} + {y_A} = 2{y_N} = - 8\end{array} \right.\) P là trung điểm của AB nên ta có \(\left\{ \begin{array}{l}{x_A} + {x_B} = 2{x_P} = - 2\\{y_A} + {y_B} = 2{y_P} = 12\end{array} \right.\) Giải hệ phương trình \(\left\{ \begin{array}{l}{x_A} + {x_B} = - 2\\{x_B} + {x_C} = 4\\{x_C} + {x_A} = 0\end{array} \right.\) ta được xA = -3 Giải hệ phương trình \(\left\{ \begin{array}{l}{y_A} + {y_B} = 12\\{y_B} + {y_C} = 6\\{y_C} + {y_A} = - 8\end{array} \right.\) ta được \({y_A}= -1\) Vậy \(A(–3 ; –1)\). HocTot.XYZ
|