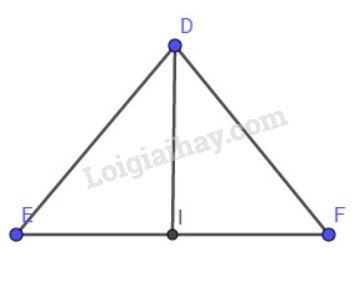
Bài 30 trang 67 SGK Hình học 10Cho tam giác DEF có DE = DF =10cm và EF = 12cm. Gọi I là trung điểm của cạnh EF. Đoạn thẳng DI có độ dài là: Đề bài Cho tam giác \(DEF\) có \(DE = DF =10cm\) và \(EF = 12cm\). Gọi \(I\) là trung điểm của cạnh \(EF\). Đoạn thẳng \(DI\) có độ dài là: A. \(6,5 cm\) B. \(7cm\) C. \(8cm\) D. \(4cm\) Video hướng dẫn giải Phương pháp giải - Xem chi tiết Áp dụng công thức tính độ dài đường trung tuyến \(m_a^2 = \frac{{2\left( {{b^2} + {c^2}} \right) - {a^2}}}{4}\) Lời giải chi tiết
Ta có: \(DI\) là đường trung tuyến của tam giác \(DEF\) Áp dụng công thức tính độ dài đường trung tuyến: \(\eqalign{ Vậy chọn C. Cách khác: Các em cũng có thể tính DI dựa vào định lý Pita go trong tam giác vuông DIE. Cụ thể: DI là đường trung tuyến của tam giác cân DEF nên DI cũng là đường cao trong tam giác. Tam giác DIE vuông tại I có DE=10, \(EI = \frac{1}{2}EF = \frac{1}{2}.12 = 6\) Theo pitago ta có: \(D{I^2} = D{E^2} - E{I^2} = {10^2} - {6^2} = 64 \) \(\Rightarrow DI = 8\left( {cm} \right)\) HocTot.XYZ
|