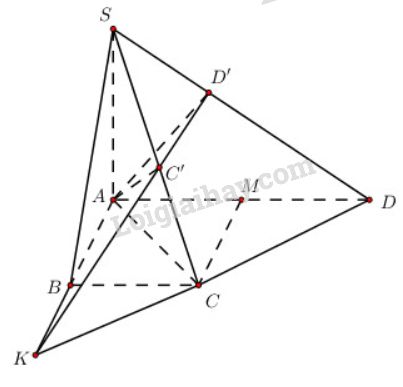
Bài 7 trang 126 SGK Hình học 11Cho hình thang ABCD vuông tại A và B, có AD = 2a, AB = BC = a. Trên tia Ax vuông góc với mặt phẳng (ABCD) lấy một điểm S. Đề bài Cho hình thang \(ABCD\) vuông tại \(A\) và \(B\), có \(AD = 2a, AB = BC = a\). Trên tia \(Ax\) vuông góc với mặt phẳng \((ABCD)\) lấy một điểm \(S\). Gọi \(C',D'\) lần lượt là hình chiếu vuông góc của \(A\) trên \(SC\) và \(SD\) . Chứng minh rằng : a) \(\widehat {SBC} = \widehat {SC{\rm{D}}} = {90^0}\) b) \(AD’, AC’\) và \(AB\) cùng nằm trên một mặt phẳng. c) Chứng minh rằng đường thẳng \(C’D’\) luôn luôn đi qua một điểm cố định khi \(S\) di động trên tia Ax. Video hướng dẫn giải Phương pháp giải - Xem chi tiết a) Chứng minh \(BC \bot \left( {SAB} \right);\,\,CD \bot \left( {SCD} \right)\). b) Chứng minh cả ba đường thẳng \(AB;AC';AD'\) cùng vuông góc với \(SD\), từ đó kết luận chúng cùng thuộc mặt phẳng đi qua A và vuông góc với \(SD\). c) Chứng minh ba đường thẳng CD, AB, C'D' đồng quy dựa vào tính chất: Giao tuyến của ba mặt phẳng phân biệt thì đồng quy hoặc đôi một song song. Lời giải chi tiết
a) Ta có: \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot BC\) \(\left. \matrix{SA \bot BC \hfill \cr AB \bot BC \hfill \cr} \right\} \Rightarrow SB \bot BC\) (định lí 3 đường vuông góc) \( \Rightarrow \widehat {SBC} = {90^0}\) \( \Rightarrow \Delta SBC\) vuông tại \(B\). Gọi \(M\) là trung điểm của \(AD\). Tứ giác \(ABCM\) có \(AB//=CM\) nên là hình bình hành. Lại có \(\widehat A = {90^0},AB = CB\) nên \(ABCM\) là hình vuông \(\Rightarrow CM = a \Rightarrow CM = {1 \over 2}A{\rm{D}}\) Tam giác \(ACD\) có trung tuyến \(CM\) bằng \({1 \over 2}\) cạnh tương ứng nên nó là tam giác vuông, hay tam giác \(ACD\) vuông tại \(C\) có \(AC ⊥ CD\) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot CD\) \(\left. \matrix{ \(\Rightarrow \widehat {SC{\rm{D}}} = {90^0}\) \( \Rightarrow \Delta SCD\) vuông tại \(C\). b) Ta có : \(\left. \matrix{ \(\left. \matrix{ Kết hợp với \( AC’ ⊥ SC\) suy ra \(AC'\bot (SCD)\) \(\left. \matrix{AC' \bot \left( {SC{\rm{D}}} \right) \hfill \cr S{\rm{D}} \subset \left( {SC{\rm{D}}} \right) \hfill \cr} \right\} \Rightarrow AC' \bot S{\rm{D\,\,\,\,\,(2)}}\) Giả thiết cho \(AD’ ⊥ SD\) (3) Từ (1), (2), (3) ta thấy ba đường thẳng \(AB, AD’, AC’\) cùng vuông góc với \(SD\) và chúng cùng đi qua \(A\). Vậy chúng cùng nằm trong mặt phẳng \(( P)\) đi qua \(A\) và vuông góc với \(SD\). c) Gọi \(K\) là giao điểm của \(C’D’\) với \(AB\). \(K ∈ C’D’ ⇒ K ∈ (SCD)\) \(K ∈ AB ⇒ K ∈ (ABCD)\) \(⇒ K\) là giao điểm của hai mặt phẳng \((SCD)\) và \((ABCD)\) Mà \(\left( {SCD} \right) \cap \left( {ABCD} \right) = CD\)\(\Rightarrow K \in CD\). Vậy ba đường thẳng \(AB, CD, C’D’\) đồng quy tại \(K\) và \(AB, CD\) cố định suy ra \(K\) cố định. Vậy khi \(S\) chạy trên \(Ax\) thì \(C’D’\) luôn đi qua điểm cố định là giao điểm \(K\) của \(AB\) và \(CD\). hoctot.xyz
|