Nội dung từ Loigiaihay.Com
Câu hỏi:
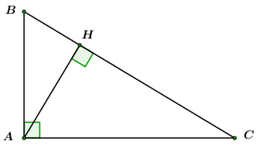
Cho \(\Delta ABC\) vuông tại \(A,\) có \(BC = 24\,cm\) và đường cao \(AH.\) Biết \(AB = \frac{2}{3}AC.\)
Câu 1:
Tính số đo các góc \(B,\,\,C\) của \(\Delta ABC\).
- A \(\angle B \approx {33^0}42',\,\,\angle C \approx {56^0}18'\)
- B \(\angle B \approx {56^0}18',\,\,\angle C \approx {33^0}42'\)
- C \(\angle B \approx {56^0}42',\,\,\angle C \approx {33^0}18'\)
- D \(\angle B \approx {56^0}20',\,\,\angle C \approx {33^0}40'\)
Phương pháp giải:
Sử dụng các công thức tỉ số lượng giác của góc nhọn trong tam giác vuông.
Lời giải chi tiết:
Ta có: \(\frac{{AB}}{{AC}} = \frac{2}{3} \Leftrightarrow AB = \frac{2}{3}AC.\)
\(\begin{array}{l} \Rightarrow \tan \angle B = \frac{{AC}}{{AB}} = \frac{3}{2} \Rightarrow \angle B \approx {56^0}18'\\ \Rightarrow \angle C = {90^0} - \angle B = {90^0} - {56^0}18' = {33^0}42'.\end{array}\)
Câu 2:
Tính độ dài \(AC\).
- A \(AC = \frac{{72\sqrt {13} }}{{13}}\,\,cm\)
- B \(AC = 72cm\)
- C \(AC = 72\sqrt {13} \,\,cm\)
- D \(AC = \frac{{72}}{{13}}\,\,cm\)
Phương pháp giải:
Sử dụng định lý Pitago trong tam giác vuông để làm bài.
Lời giải chi tiết:
Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) ta có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} \Leftrightarrow {24^2} = {\left( {\frac{2}{3}AC} \right)^2} + A{C^2}\\ \Leftrightarrow \frac{{13}}{9}A{C^2} = 576 \Leftrightarrow A{C^2} = \frac{{5184}}{{13}} \Rightarrow AC = \frac{{72\sqrt {13} }}{{13}}\,\,cm.\end{array}\)
Câu 3:
Tính độ dài \(AB\).
- A \(AB = \frac{{48\sqrt {13} }}{{13}}\,\,cm.\)
- B \(AB = 48\sqrt {13} \,\,cm\)
- C \(AB=48cm\)
- D \(AB = \frac{{144}}{{\sqrt {39} }}\,\,cm\)
Phương pháp giải:
Cộng trừ độ dài các đoạn thẳng.
Lời giải chi tiết:
Ta có: \( AB = \frac{2}{3}.\frac{{72\sqrt {13} }}{{13}}\, = \frac{{144\sqrt {13} }}{{39}} = \frac{{48\sqrt {13} }}{{13}}\,\,cm.\)
Câu 4:
Tính độ dài \(AH \).
- A \(AH = \frac{{144}}{{39}}\,\,cm\)
- B \(AH = \frac{{169}}{{18}}\,\,cm\)
- C \(AH = \frac{{144}}{{13}}\,\,cm\)
- D \(AH = \frac{{144}}{{\sqrt {13} }}\,\,cm\)
Phương pháp giải:
Sử dụng hệ thức lượng trong tam giác vuông để làm bài.
Lời giải chi tiết:
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:
\(AH.BC = AB.AC \Leftrightarrow AH = \frac{{AB.AC}}{{BC}} = \frac{{\frac{{144\sqrt {13} }}{{39}}.\frac{{72\sqrt {13} }}{{13}}}}{{24}} = \frac{{144}}{{13}}\,\,cm.\)