Câu hỏi trước
Nội dung từ Loigiaihay.Com
Câu hỏi:
Giải bất phương trình \({x^2} - x - 20 > 2(x - 11)\)
- A \(\left( {1;\,\,2} \right)\)
- B \(\left( { - \infty ;\,\,2} \right)\)
- C \(\left( { - \infty ;\,\,1} \right) \cup \left( {2; + \infty } \right)\)
- D \(\left( {1; + \infty } \right)\)
Phương pháp giải:
Đưa về phương trình tích và lập bảng xét dấu.
Lời giải chi tiết:
\(\begin{array}{l}{x^2} - x - 20 > 2\left( {x - 11} \right)\\ \Leftrightarrow {x^2} - x - 20 > 2x - 22\\ \Leftrightarrow {x^2} - 3x + 2 > 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 2} \right) > 0\end{array}\)
Xét dấu của \(\left( {x - 1} \right)\left( {x - 2} \right)\). Ta có bảng xét dấu: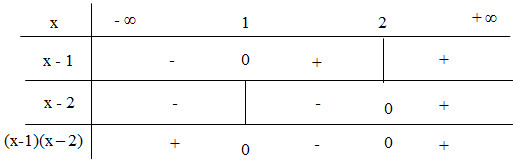 
Vậy tập nghiệm của bất phương trình là: \(\left( { - \infty ;1} \right) \cup \left( {2; + \infty } \right)\)
Chọn C.