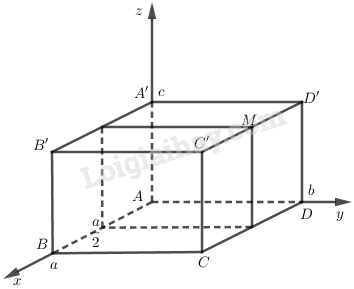
Trả lời câu hỏi 2 trang 64 SGK Hình học 12Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’... Đề bài Trong không gian \(Oxyz\), cho hình hộp chữ nhật \(ABCD.A’B’C’D’\) có đỉnh \(A\) trùng với gốc \(O\), có \(\overrightarrow {AB} ;\,\overrightarrow {AD} ;\,\overrightarrow {{\rm{AA}}'} \) theo thứ tự cùng hướng với \(\overrightarrow i ;\,\overline j ;\,\overrightarrow k \) và có \(AB = a, AD = b, AA’ = c\). Hãy tính tọa độ các vecto \(\overrightarrow {AB} ;\,\overrightarrow {AC} ;\,\overrightarrow {AC'} ;\,\overrightarrow {AM} \) với \(M\) là trung điểm của cạnh \(C’D’\). Video hướng dẫn giải Phương pháp giải - Xem chi tiết Vẽ hình, xác định tọa độ các véc tơ. + Nếu A trùng với gốc tọa độ thì \(\overrightarrow {AB} \) có tọa độ là tọa độ điểm \(B\) + Dựa vào độ dài cạnh để xác định tọa đô các đỉnh Lời giải chi tiết Ta có: \(A\left( {0;0;0} \right)\) trùng với gốc tọa độ. Vì \(B \in Ax \text{ nên} B\left( {a;0;0} \right)\) (trong đó a là độ dài đại số của đoạn \(AB\)) Tương tự ta suy ra các đỉnh \(D\left( {0;b;0} \right),A'\left( {0;0;c} \right)\). Điểm \(C\) thuộc mp \((Axy)\) nên tọa độ \(C\) có dạng \((x,y, 0)\) trong đó \(x\) là độ dài đại số của \(AB\), \(y\) là độ dài đại số của \(AD\) suy ra \(C\left( {a;b;0} \right)\) Tương tự ta suy ra \(D'\left( {0;b;c} \right),\) \(B'\left( {a;0;c} \right)\) Riêng \(C' \left( {a;b;c} \right)\), \(M\left( {\dfrac{a}{2};b;c} \right)\). Vậy \(\overrightarrow {AB} = \left( {a;0;0} \right),\) \(\overrightarrow {AC} = \left( {a;b;0} \right),\) \(\overrightarrow {AC'} = \left( {a;b;c} \right)\), \(\overrightarrow {AM} = \left( {\dfrac{a}{2};b;c} \right)\).
HocTot.XYZ
|