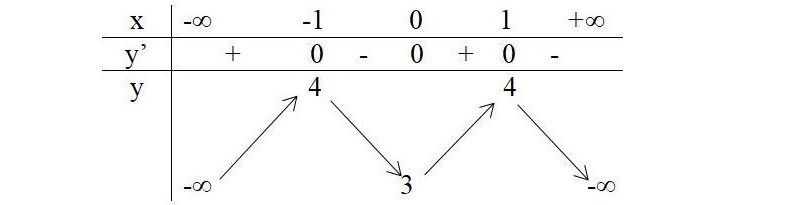
Trả lời câu hỏi 4 trang 36 SGK Giải tích 12Khảo sát sự biến thiên và vẽ đồ thị của hàm số ... Đề bài Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = - {x^4} + 2{x^2}+ 3.\) Bằng đồ thị, biện luận theo \(m\) số nghiệm của phương trình \(- {x^4} + 2{x^2}+ 3=m.\) Video hướng dẫn giải Lời giải chi tiết * Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = - {x^4} + 2{x^2}+ 3.\) 1.TXĐ: \(D = \mathbb R\). 2. Sự biến thiên: \(\eqalign{ \(y = - 4{x^3}\; + {\rm{ }}4x.\) Cho \(y’ = 0 ⇒ x = 0\) hoặc \(x = ±1.\) Bảng biến thiên
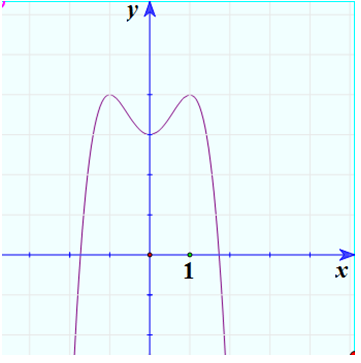
Hàm số đồng biến trên: \(\left( { - \infty , - 1} \right);\;\left( {0,1} \right).\) Hàm số nghịch biến trên: \(\left( { - 1,0} \right){\rm{; }}\left( {1, + \infty } \right).\) Hàm số đạt cực đại bằng 4 tại \(x = -1\) và \(x = 1.\) Hàm số đạt cực tiểu bằng 3 tại \(x = 0.\) Đồ thị * Giải biện luận phương trình \(- {x^4} + 2{x^2}+ 3=m.\) Số giao điểm của hai đồ thị \(y = - {x^4} + 2{x^2}+ 3\) và \(y = m\) là số nghiệm của phương trình trên. Với \(m > 4\) Hai đồ thị không giao nhau nên phương trình vô nghiệm. Với \(m = 4\) hoặc \(m < 3:\) Hai đồ thị giao nhau tại 2 điểm phân biệt nên phương trình có hai nghiệm phân biệt. Với \(m = 3\). Hai đồ thị giao nhau tại 3 điểm phân biệt nên phương trình có ba nghiệm phân biệt. Với \(3 < m < 4:\) Hai đồ thị giao nhau tại 4 điểm phân biệt nên phương trình có bốn nghiệm phân biệt. HocTot.XYZ
|