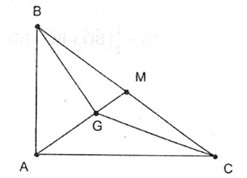
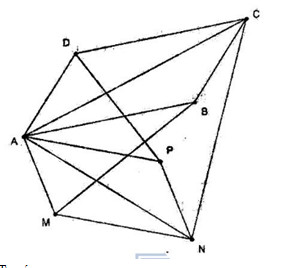
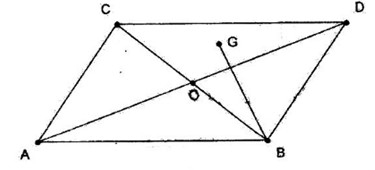
Đề kiểm tra 15 phút - Chương 1 - Đề số 1 - Hình học 10Đáp án và lời giải chi tiết Đề kiểm tra 15 phút - Chương 1 - Đề số 1 - Hình học 10 Đề bài Câu 1. Cho tam giác ABC vuông tại A có trọng tâm là G. Biết rằng AB=6 và AC=8. Tính độ dài của các véc tơ \(\overrightarrow {GB} - \overrightarrow {GC} \) và \(\overrightarrow {GB} + \overrightarrow {GC} \). Câu 2. Cho hai hình bình hành ABCD và AMNP có chung đỉnh A. Chứng minh rằng \(\overrightarrow {BM} + \overrightarrow {DP} = \overrightarrow {CN} \). Câu 3. Cho hình bình hành ABDC tâm O. Gọi G là trọng tâm tam giác OCD. Hãy biểu thị \(\overrightarrow {BG} \) theo các véc tơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \). Lời giải chi tiết Câu 1. Theo định lí Pitago ta có: \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {36 + 64} = 10\) Ta có \(\overrightarrow {GB} - \overrightarrow {GC} = \overrightarrow {CB} \) . Suy ra \(\left| {\overrightarrow {GB} - \overrightarrow {GC} } \right| = \left| {\overrightarrow {CB} } \right| = CB = 10\) Gọi M là trung điểm BC. Ta có \(\overrightarrow {GB} + \overrightarrow {GC} = 2\overrightarrow {GM} \) . Mà \(GM = \dfrac{1 }{3}AM = \dfrac{1 }{6}BC = \dfrac{10} {6} = \dfrac{5 }{ 3}\) Vậy \(\left| {\overrightarrow {GB} + \overrightarrow {GC} } \right| = \left| {2\overrightarrow {GM} } \right| = 2GM = \dfrac{10}{3}\) Câu 2. Ta có \(\overrightarrow {BM} + \overrightarrow {DP} \) \(= \overrightarrow {AM} - \overrightarrow {AB} + \overrightarrow {AP} - \overrightarrow {AD} \) \( = \left( {\overrightarrow {AM} + \overrightarrow {AP} } \right) - \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) \) \(= \overrightarrow {AN} - \overrightarrow {AC} = \overrightarrow {CN} \) Câu 3. Ta có: \(\eqalign{ & \overrightarrow {BG} = \dfrac{1}{3}\left( {\overrightarrow {BO} + \overrightarrow {BC} + \overrightarrow {BD} } \right) \cr } \) \(\begin{array}{l} HocTot.XYZ
|