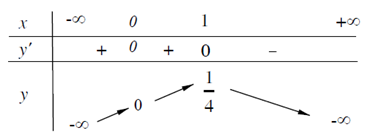
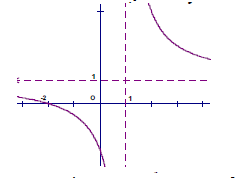
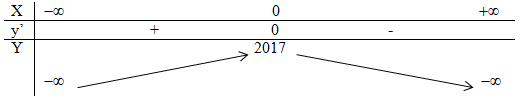Đề kiểm tra 15 phút - Đề số 4 - Chương I - Giải Tích 12Đáp án và lời giải chi tiết Đề thi kiểm tra 15 phút - Đề số 4 - Chương I - Giải Tích 12 Đề bài Câu 1. Tính giá trị lớn nhất của hàm số \(f(x) = - {x^4} - 3{x^2} + 2017\) trên R. A. \(\mathop {\max }\limits_R f(x) = 2017\) B. \(\mathop {\max }\limits_R f(x) = 2016\) C. \(\mathop {\max }\limits_R f(x) = 2015\) D. \(\mathop {\max }\limits_R f(x) = 2014\) Câu 2. Cho hàm số y=f(x) có bảng biến thiên như sau: Khẳng định nào sau đây đúng? A. Hàm số nghịch biến trên \(( - \infty ;1)\). B. Hàm số đồng biến trên \(( - \infty ;1)\). C. Hàm số nghịch biến trên \(\left( { - \infty ;{1 \over 4}} \right)\). D. Hàm số đồng biến trên \(\left( { - \infty ;{1 \over 4}} \right)\). Câu 3. Cho hàm số y=f(x) có \(\mathop {\lim }\limits_{x \to + \infty } f(x) = 2\,,\,\,\mathop {\lim }\limits_{x \to - \infty } f(x) = - 2\). Khẳng định nào sau đây đúng ? A. Đồ thị hàm số đã cho có đúng một tiệm cận ngang. B. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y = 2 và y = - 2. C. Đồ thị hàm số đã cho không có tiệm cận ngang. D. Đồ thị hàm số đã cho ó hai tiệm cận ngang là các đường thẳng x = 2 và x = - 2. Câu 4. Tìm điều kiện của m để hàm số \(y = \dfrac{1 }{4}{x^4} - 2m{x^2} + 3\) không có cực đại. A. m > 0 B. m < 0 C. \(m \ge 0\) D. \(m \le 0\). Câu 5. Phương trình tiếp tuyến của đồ thị hàm số \(y = {x^3} - 3{x^2} + 1\) tại điểm A(3 ; 1) là: A. \(y = - 9x - 26\) B. \(y = 9x - 26\) C. \(y = - 9x - 3\) D. \(y = 9x + 2\) Câu 6. Đồ thị hàm số \(y = \dfrac{{2x - 1}}{{ - x + 1}}\) có tiệm cận đứng A. x = 1 B. y = 1 C. x = - 1 D. y = - 2. Câu 7. Cho hàm số \(y = x + \cos x\) Tìm phát biểu đúng: A. Hàm số đồng biến trên R. B. Hàm số nghịch biến trên \((0; + \infty )\). C. Hàm số nghịch biến trên R. D. Hàm số đồng biến trên \(( - \infty ;0)\). Câu 8. Đồ thị sau đây là của hàm số nào ? A. \(y = \dfrac{{x + 1}}{{x - 1}}\) B. \(y = \dfrac{{x - 2}}{{1 - x}}\) C. \(y = \dfrac{{x + 2}}{{x - 1}}\) D. \(y = \dfrac{{x + 2}}{{1 - x}}\). Câu 9. Đồ thị hàm số nào có đường tiệm cận ngang? A. \(y = {x^4} - {x^2} + 3\) B. \(y = \dfrac{{x - 2}}{{{x} + 2}}\) C. \(y = {x^3} - 2{x^2} + 3\) D. \(y = \dfrac{{{x^2} + 1}}{{x - 1}}\) Câu 10. Tích các tung độ giao điểm của hai đồ thị hàm số \(y = {x^3} - {x^2} - 2x + 3,\,\,\,y = {x^2} - x + 1\) A. 3 B. 9 C. 10 D. – 2 Lời giải chi tiết
Câu 1. \(f'(x) = - 4{x^3} - 6x = 0\,\, \Rightarrow x = 0\)
Vậy đồ thị hàm số đạt cực đại tại \(x = 0 \). Do đó, hàm số đạt giá trị lớn nhất là \( f(0)=2017.\) Chọn đáp án A. Câu 2. Từ bbt ta thấy hàm số đồng biến trên \(\left( { - \infty ;1} \right)\) Chọn B. Câu 3. Vì \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2\) và \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - 2\) nên các đường thẳng \(y = 2\) và \(y = - 2\) là các đường TCN của đồ thị hàm số. Chọn B. Câu 4. Ta có \(y' = {x^3} - 4mx\) \(y' = 0\,\, \Leftrightarrow \,\left[ \begin{array}{l}{x^2} = 4m\\x = 0\end{array} \right.\) Vậy để hàm số không có cực đại thì phương trình \({x^2} - 4m = 0\) vô nghiệm hoặc có một nghiệm bằng 0 tức là \(4m \le 0\) hay \(m \le 0\). Chọn đáp án D. Câu 5. Ta có \(y' = 3{x^2} - 6x,\,\,y'(3) = 9\) . Vậy phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm A(3 ; 1) là \(y = 9\left( {x - 3} \right) + 1 = 9x - 26\) Chọn đáp án B. Câu 6. Ta có \(\begin{array}{l}D = R\backslash \{ 1\} \\\mathop {\lim }\limits_{x \to {1^ + }} \dfrac{{2x - 1}}{{ - x + 1}} = \, - \infty \,\,\,\,\,\,,\\\mathop {\lim }\limits_{x \to {1^ - }} \dfrac{{2x - 1}}{{ - x + 1}} = \,\, + \infty \end{array}\) Do đó đường tiệm cận đứng của đồ thị hàm số là x = 1. Chọn đáp án A. Câu 7. Ta có \(y' = 1 - \sin x \ge 0,\,\forall x \in R\) . Do đó hàm số đồng biến trên R. Chọn đáp án A. Câu 8. Đồ thị hàm số có đường tiệm cận đứng là x = 1, đường tiệm cận ngang là y = 1. Do đó, loại đáp án B, D. Điểm (-2; 0) thuộc đồ thị hàm số nên chỉ có C thỏa mãn. Chọn đáp án C. Câu 9. Ta có \(\mathop {\lim }\limits_{x \to + \infty } \dfrac{{x - 2}}{{x + 2}} = 1 = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{x - 2}}{{x + 2}}\) Chọn đáp án B. Câu 10. Phương trình hoành độ giao điểm: \(\begin{array}{l}{x^3} - {x^2} - 2x + 3 = {x^2} - x + 1\\ \Leftrightarrow \,\left[ \begin{array}{l}x = - 1\\x = 1\\x = 2\end{array} \right.\,\\y( - 1) = 3,\,\,y(1) = 1,\,y(2) = 3\end{array}\) Vậy tích các tung độ giao điểm của hai đồ thị đã cho là 9. Chọn đáp án B. Chú ý: Các em bấm máy tính, chức năng MODE 5 4 để giải phương trình bậc ba. HocTot.XYZ
|