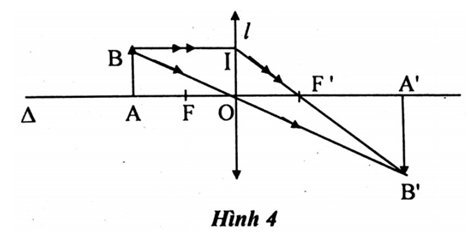
Đề kiểm tra 45 phút (1 tiết) - Đề số 5 - Chương 3 - Vật lí 9Giải Đề kiểm tra 45 phút (1 tiết) - Đề số 5 - Chương 3 - Vật lí 9 Đề bài Câu 1. Máy phát điện xoay chiều bắt buộc phải gồm các bộ phận chính nào để có thế tạo ra dòng điện? Câu 2. Một máy phát điện xoay chiều có hiệu điện thế xoay chiều ở hai cực là 220V. Muốn tải điện đi xa người ta phải tăng hiệu điện thế thành 15400V. Hỏi phải dùng loại máy biến thế với các cuộn dây có số vòng dây theo tỷ lệ như thế nào? Cuộn dây nào mắc với hai đầu máy phát điện? Câu 3. Một máy biến thế gồm cuộn sơ cấp có 1000 vòng, cuộn thứ cấp có 10000 vòng đặt ở đầu một đường dây tải điện để truyền đi một công suất điện là 11000kW. Biết hiệu điện thế hai đầu cuộn thứ cấp là 110kV a) Tính hiệu điện thế đặt ở hai đầu cuộn sơ cấp b) Cho điện trở của toàn bộ đường dây là 50Ω. Tính công suất hao phí do tỏa nhiệt trên đường dây. Câu 4: Dựng ảnh của vật bởi thấu kính hội tụ có tiêu cự f = 4cm, khoảng cách từ vật đến thấu kính bằng 8cm. Chứng minh \(d’=d; h’=h\), lập công thức \(f = \dfrac{{d + d'}}{4}\). Lời giải chi tiết Câu 1 : Các bộ phận chính để có thể tạo ra dòng điện trong các máy phát điện xoay chiều gồm: Cuộn dây dẫn và nam châm. Trong các máy phát điện nhỏ thường dùng nam châm vĩnh cửu, trong các máy lớn thường dùng các nam châm điện. Câu 2 : Ta có \(\dfrac{{{U_1}}}{{{U_2}}} = \dfrac{{{N_1}}}{{{N_2}}} = \dfrac{{15400}}{{220}} = 70\) Cuộn dây có ít vòng dây mắc với hai đầu máy phát điện. Câu 3 : a. Tính hiệu điện thế đặt vào hai đầu cuộn sơ cấp : Ta có \(\dfrac{{{U_1}}}{{{U_2}}} = \dfrac{{{N_1}}}{{{N_2}}}\) \(\Rightarrow {U_1} = \dfrac{{{U_2}{N_1}}}{{{N_2}}} = \dfrac{{110000.1}}{{10}} \)\(\,= 11000\,V\) Cuộn dây có ít vòng dây mắc với hai đầu máy phát điện. b. Công suất hao phí do tỏa nhiệt trên đường - Cường độ dòng điện qua dây: \(I = \dfrac{P}{U} = \dfrac{{11000}}{{110}} = 100\,\,A\) Công suất hao phí: \({P_{hp}} = {I^2}.R = {100^2}.50 = 500000W \)\(\;= 500kW.\) Câu 4 : Xem hình 4 Ta có \(BI = AO = 2f = 2OF’\) => OF’ là đường trung bình của tam giác B’BI \(d=d’ = 2f \Rightarrow d + d' = 4f \) \(\Rightarrow f = \dfrac{{d + d'}}{4}\) HocTot.XYZ
|