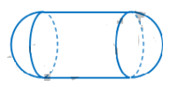
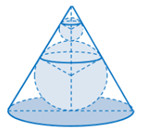
Đề số 7 - Đề thi thử THPT Quốc gia môn ToánĐáp án và lời giải chi tiết Đề số 7 - Đề thi thử THPT Quốc gia môn Toán đề trắc nghiệm Đề bài Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, \(AB = 2a,BC = a.\) Các cạnh bên của hình chóp bằng nhau và bằng \(a\sqrt 2 .\) Gọi M, N lần lượt là trung điểm của các cạnh AB, CD. K là điểm trên cạnh AD sao cho \(KD = 2KA.\) Tính khoảng cách giữa hai đường thẳng MN và SK. A.\(\dfrac{{3a}}{2}\) B.\(\dfrac{{a\sqrt 2 }}{3}\) C.\(\dfrac{{a\sqrt 3 }}{7}\) D.\(\dfrac{{a\sqrt {21} }}{7}\) Câu 2: Phương trình \(m\sin x + 3\cos x = 5\) có nghiệm khi và chỉ khi: A.\(m \le 2\) B.\(\left| m \right| \ge 4\) C.\(\left| m \right| \le 4\) D.\(m \ge 2\) Câu 3: Một người gửi số tiền 100 triệu đồng vào một ngân hàng với lãi suất \(7,4\% \)/ năm. Biết rằng nếu không rút tiền ra khỏi ngan hàng thì cứ sau mỗi năm, số tiền sẽ được nhập vào vốn ban đầu (người ta gọi đó là lãi kép). Để lãnh được số tiền ít nhất 250 triệu thì người đó cần gửi trong khoảng thời gian bao nhiêu năm? (nếu trong khoảng thời gian này không rút tiền ra và lãi suất không thay đổi) A.13 năm B.12 năm C.14 năm D.15 năm Câu 4: Tính đạo hàm của hàm số sau: \(f(x) = \ln \left( {{x^2} + 1} \right)\) A.\(f'(x) = \ln \left( {{x^2} + 1} \right)\) C. \(f'(x) = \dfrac{1}{{{x^2} + 1}}\) B. \(f'(x) = \ln 2x\) D.\(f'(x) = \dfrac{{2x}}{{{x^2} + 1}}\) Câu 5: Cho phương trình:\(\left( {m - 1} \right)\log _{\dfrac{1}{2}}^2{\left( {x - 2} \right)^2} \)\(\,+ 4\left( {m - 5} \right){\log _{\dfrac{1}{2}}}\dfrac{1}{{x - 2}} + 4m - 4 = 0\) (với m là tham số). Gọi \(S = \left[ {a;b} \right]\) là tập các giá trị của m để phương trình có nghiệm trên đoạn \(\left[ {\dfrac{5}{2},4} \right]\). Tính \(a + b.\) A.\(\dfrac{7}{3}\) B.\( - \dfrac{2}{3}\) C.\( - 3\) D.\(\dfrac{{1034}}{{273}}.\) Câu 6: Cho hàm số \(\left( {{C_m}} \right):y = {x^3} + m{x^2} - 9x - 9m.\) Tìm m để \(\left( {{C_m}} \right)\) tiếp xúc với Ox: A.\(m = \pm 3\) B. \(m = \pm 4\) C. \(m = \pm 1\) D. \(m = \pm 2\) Câu 7: Một cái bồn chứa nước gồm hai nửa hình cầu và một hình trụ (như hình vẽ). Đường sinh của hình trụ (như hình vẽ). Đường sinh của hình trụ bằng hai lần đường kính của hình cầu. Biết thể tích của bồn chứa nước là \(\dfrac{{128\pi }}{3}\left( {{m^3}} \right)\).Tính diện tích xung quanh của cái bồn chứa nước theo đơn vị \({m^2}.\)
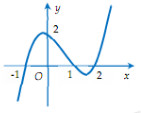
A.\(48\pi \left( {{m^2}} \right)\) B. \(40\pi \left( {{m^2}} \right)\) C. \(64\pi \left( {{m^2}} \right)\) D. \(50\pi \left( {{m^2}} \right)\) Câu 8: Cho hàm số \(y = f(x)\) xác định và có đạo hàm \(f'\left( x \right)\). Đồ thị của hàm số \(f'\left( x \right)\)như hình dưới đây. Khẳng định nào sau đây là đúng?
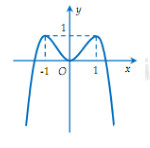
A.Hàm số \(y = f(x)\) có ba điểm cực trị. B. Hàm số \(y = f(x)\) đồng biến trên khoảng \(\left( { - \infty ;2} \right).\) C.Hàm số \(y = f(x)\)nghịch biến trên khoảng \(\left( {0;1} \right)\). D. Hàm số \(y = f(x)\)đồng biến trên khoảng \(\left( { - \infty ; - 1} \right)\). Câu 9: Cho hình chóp SABC có SB = SC = BC = CA=a. Hai mặt (ABC) và (ASC) cùng vuông góc với (SBC). Tính thể tích hình chóp. A.\(\dfrac{{{a^3}\sqrt 3 }}{4}\) B. \(\dfrac{{{a^3}\sqrt 3 }}{{12}}\) C. \(\dfrac{{{a^3}\sqrt 2 }}{{12}}\) D. \(\dfrac{{{a^3}\sqrt 3 }}{6}\) Câu 10: Cho lăng trụ đứng \(ABC.A'B'C'\) có \(AB = AC = BB' = a,\widehat {BAC} = {120^ \circ }\). Gọi I là trung điểm của \(CC'\). Tính cosin của góc tạo bởi hai mặt phẳng (ABC) và \(\left( {AB'I} \right).\) A.\(\dfrac{{\sqrt 2 }}{2}\) B.\(\dfrac{{3\sqrt 5 }}{{12}}\) C.\(\dfrac{{\sqrt {30} }}{{10}}\) D.\(\dfrac{{\sqrt 3 }}{2}\) Câu 11: Đồ thị hàm số \(y = \dfrac{{\sqrt {{x^2} - x + 2} - 2}}{{{x^2} - 1}}\) có bao nhiêu đường tiệm cận đứng? A.0 B.2 C.3 D.1 Câu 12: Tìm giá trị nhỏ nhất của biểu thức:\(F = \dfrac{{{a^4}}}{{{b^4}}} + \dfrac{{{b^4}}}{{{a^4}}} - \left( {\dfrac{{{a^2}}}{{{b^2}}} + \dfrac{{{b^2}}}{{{a^2}}}} \right) + \dfrac{a}{b} + \dfrac{b}{a}\) với \(a,b \ne 0\) A.\(MinF = 10\) B. \(MinF = 2\) C. \(MinF = - 2\) D. F không có GTNN Câu 13: Cho tập A có 20 phần tử. Hỏi tập A có bao nhiêu tập hợp con khác rỗng mà có số phần tử chẵn A.\({2^{20}} + 1\) B.\({2^{20}}\) C.\(\dfrac{{{2^{20}}}}{2} - 1\) D.\({2^{19}}\) Câu 14: Cho hàm số \(y = {x^3} - 3{x^2} + 5x - 2\) có đồ thị (C). Viết phương trình tiếp tuyến của đồ thị (C) có hệ số góc nhỏ nhất. A.\(y = 2x - 2\) B. \(y = 2x - 1\) C. \(y = - 2x\) D. \(y = - 2x + 1\) Câu 15: Cho một hình trụ (T) có chiều cao và bán kính đều bằng 3a. Một hình vuông ABCD có hai cạnh AB, CD lần lượt là hai dây cung của hai đường tròn đáy, cạnh AD, BC không phải là đường sinh của hình trụ (T). Tính cạnh của hình vuông này. A.\(3a\sqrt 5 \) B.\(6a\) C.\(\dfrac{{3a\sqrt {10} }}{2}\) D.\(3a\) Câu 16: Cắt một hình nón bằng một mặt phẳng đi qua trục của nó ta được thiết diện là một tam giác vuông cân có cạnh huyền bằng a, diện tích xung quanh của hình nón là: A.\({S_{xq}} = \dfrac{{\pi {a^2}\sqrt 2 }}{4}\) B. \({S_{xq}} = \dfrac{{\pi {a^2}\sqrt 2 }}{2}\) C. \({S_{xq}} = \pi {a^2}\sqrt 2 \) D. \({S_{xq}} = \pi {a^2}\) Câu 17: Cho hàm số \((C):y = {x^3} + 3{x^2} + 1.\) Đường thẳng đi qua điểm \(A\left( { - 3;1} \right)\) và có hệ số góc bằng k. Xác định k để đường thẳng đó cắt đồ thị tại 3 điểm khác nhau A.\(0 < k < 1\) B.\(k > 0\) C.\(0 < k \ne 9\) D.\(1 < k < 9\) Câu 18: Cho hàm số \(y = \dfrac{{3x}}{{1 + 2x}}\). Khẳng định nào sau đây là khẳng định đúng? A.Đồ thị hàm số có tiệm cận ngang là \(y = \dfrac{3}{2}.\) B.Đồ thị hàm số có tiệm cận ngang là \(y = 3.\) C.Đồ thị hàm số có tiệm cận đứng là \(x = 1.\) D. Đồ thị hàm số không có tiệm cận. Câu 19: Cho \({9^x} + {9^{ - x}} = 23.\) Khi đó biểu thức \(A = \dfrac{{5 + {3^x} + {3^{ - x}}}}{{1 - {3^x} - {3^{ - x}}}} = \dfrac{a}{b}\) với \(\dfrac{a}{b}\) tối giản và \(a,b \in Z\). Tích \(a.b\) có giá trị bằng: A.8 B.10 C.\( - 8\) D.\( - 10\) Câu 20: Cho \(a,b,c\) là ba số thực dương, khác 1 và \(abc \ne 1.\) Biết \({\log _a}3 = 2,{\log _b}3 = \dfrac{1}{4}\) và \({\log _{abc}}3 = \dfrac{2}{{15}}.\) Khi đó, giá trị của \({\log _c}3\) bằng bao nhiêu? A.\({\log _c}3 = \dfrac{1}{3}\) B. \({\log _c}3 = \dfrac{1}{2}\) C. \({\log _c}3 = 3\) D. \({\log _c}3 = 2\) Câu 21: Đường cong trong hình dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? A.\(y = - {x^4} - 2{x^2} + 2\) C.\(y = - {x^4} + 2{x^2}\) B.\(y = - {x^3} + 3{x^2} + 1\) D.\(y = - {x^4} + 2{x^2} + 2\)
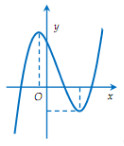
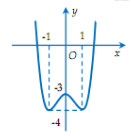
Câu 22: Giá trị lớn nhất của hàm số \(y = x\left( {2 - \ln x} \right)\) trên đoạn \(\left[ {2;3} \right]\) là A.\(\mathop {\max }\limits_{\left[ {2;3} \right]} y = 4 - 2\ln 2\) C. \(\mathop {\max }\limits_{\left[ {2;3} \right]} y = e\) B. \(\mathop {\max }\limits_{\left[ {2;3} \right]} y = 1\) D. \(\mathop {\max }\limits_{\left[ {2;3} \right]} y = - 2 + 2\ln 2\) Câu 23: Cho n là số nguyên dương, tìm n sao cho: \({1^2}{\log _a}2019 + {2^2}{\log _{\sqrt a }}2019 + ... + {n^2}{\log _{\sqrt[n]{a}}}2019 \)\(\;= {1010^2} \times {2019^2}{\log _a}2019\) A.2019 B.2018 C.2017 D.2016 Câu 24: Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình bên. Khẳng định nào sau đây đúng?
A.\(a,d > 0;b,c < 0\) C. \(a,c,d > 0;b < 0\) B. \(a,b,d > 0;c < 0\) D. \(a,b,c < 0;d > 0\) Câu 25: Tìm tổng các nghiệm của phương trình sau \({\log _{\sqrt[4]{5}}}\left( {{x^2} - 2x - 3} \right) = 2{\log _2}\left( {{x^2} - 2x - 4} \right)\) A.0 B.\( - 1\) C.2 D.3 Câu 26: Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh a và SA vuông góc đáy ABCD và mặt bên (SCD) hợp với đáy một góc \({60^ \circ }\), M là trung điểm của BC. Tính thể tích hình chóp S.ABMD A.\(\dfrac{{{a^3}\sqrt 3 }}{4}\) B. \(\dfrac{{{a^3}\sqrt 3 }}{6}\) C. \(\dfrac{{{a^3}\sqrt 3 }}{3}\) D. \({a^3}\sqrt 3 \) Câu 27: Tập hợp tất cả các giá trị của m để hàm số \(y = \dfrac{1}{3}{x^3} - \left( {m - 1} \right){x^2} + 2\left( {m - 1} \right)x - 2\) luôn tăng trên \(R\) A.\(m > 1\) C.\(2 \le m \le 3\) B.\(\left[ \begin{array}{l}m < 1\\m > 3\end{array} \right.\) D.\( - 1 \le m \le 3\) Câu 28: Trong các hàm số sau, hàm số nào nghịch biến trên khoảng \(\left( {0;\sqrt 2 } \right)\) A.\(y = \dfrac{{{x^2} + x - 1}}{{x - 1}}\) C.\(y = \dfrac{1}{2}{x^4} - 2{x^2} + 3\) B.\(y = \dfrac{{2x - 5}}{{x + 1}}\) D.\(y = \dfrac{3}{2}{x^3} - 4{x^2} + 6x + 9\) Câu 29: Phương trình:\(3\sqrt {x - 1} + m\sqrt {x + 1} = 2\sqrt[4]{{{x^2} - 1}}\) có nghiệm x khi: A.\(0 \le m \le \dfrac{1}{3}\) B.\( - 1 < m \le \dfrac{1}{3}\) C.\(m \ge \dfrac{1}{3}\) D.\( - 1 \le m \le \dfrac{1}{3}\) Câu 30: Cho hàm số \(y = f(x)\) xác định, liên tục và có đạo hàm trên đoạn \(\left[ {a;b} \right]\). Xét các khẳng định sau: 1.Hàm số f(x) đồng biến trên \((a;b)\) thì \(f'(x) > 0,\forall x \in \left( {a;b} \right)\) 2.Giả sử \(f\left( a \right) > f\left( c \right) > f\left( b \right),\forall c \in \left( {a,b} \right)\) suy ra hàm số nghịch biến trên \(\left( {a;b} \right)\) 3. Giả sử phương trình \(f'(x) = 0\) có nghiệm là \(x = m\) khi đó nếu hàm số \(f(x)\) đồng biến trên \(\left( {m,b} \right)\) thì hàm số f(x) nghịch biến trên \(\left( {a,m} \right).\) 4. Nếu \(f'(x) \ge 0,\forall x \in \left( {a,b} \right)\), thì hàm số đồng biến trên \(\left( {a,b} \right)\) Số khẳng định đúng trong các khẳng định trên là A.1 B.0 C.3 D.2 Câu 31: Người ta chế tạo ra một món đồ chơi cho trẻ em theo các công đoạn như sau: Trước tiên cho trẻ em theo các công đoạn như sau: Trước tiên, chế tạo ra một mặt nón tròn xoay có góc ở đỉnh là \(2\beta = {60^ \circ }\) bằng thủy tinh có bán kính lớn, nhỏ khác nhau sao cho 2 mặt cầu tiếp xúc với nhau và đều tiếp xúc với mặt nón. Quả cầu lớn tiếp xúc với cả mặt đáy của mặt nó. Cho biết chiều cao của mặt nón bằng 9cm. Bỏ qua bề dày của những lớp vỏ thủy tinh, hãy tính tổng thể tích của hai khối cầu.
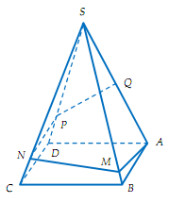
A.\(\dfrac{{25}}{3}\pi \left( {c{m^3}} \right)\) B. \(\dfrac{{112}}{3}\pi \left( {c{m^3}} \right)\) C. \(\dfrac{{40}}{3}\pi \left( {c{m^3}} \right)\) D. \(\dfrac{{10}}{3}\pi \left( {c{m^3}} \right)\) Câu 32: Cho khối chóp S.ABC có thể tích là \(\dfrac{{{a^3}}}{3}.\) Tam giác SAB có diện tích là \(2{a^2}.\) Tính khoảng cách d từ C đến mặt phẳng (SAB). A.\(d = a\) B.\(d = \dfrac{{2a}}{3}\) C.\(d = 2a\) D.\(d = \dfrac{a}{2}\) Câu 33: Cho nửa đường tròn đường kính \(AB = 2R\) và một điểm C thay đổi trên nửa đường tròn đó, đặt \(\widehat {CAB} = \alpha \) và gọi H là hình chiếu vuông góc của C trên AB. Tìm \(\alpha \) sao cho thể tích của vật thể tròn xoay tạo thành khi xoay tam giác ACH quanh trục AB đạt giá trị lớn nhất: A.\(\alpha = {60^ \circ }\) B.\(\alpha = {45^ \circ }\) C.\(\alpha = \arctan \dfrac{1}{{\sqrt 2 }}\) D.\(\alpha = {30^ \circ }\) Câu 34: Tìm m để phương trình sau có nghiệm: \(\sqrt {3 + x} + \sqrt {6 - x} - \sqrt {\left( {3 + x} \right)\left( {6 - x} \right)} = m\) A.\(0 \le m \le 6\) B.\(3 \le m \le 3\sqrt 2 \) C.\( - \dfrac{1}{2} \le m \le 3\sqrt 2 \) D.\(3\sqrt 2 - \dfrac{9}{2} \le m \le 3\) Câu 35: Cho tam giác ABC vuông tại A, \(AB = a,BC = 2a.\) Tính thể tích khối nón nhận được khi quay tam giác ABC quanh trục BC. A.\(\dfrac{{\pi {a^3}}}{2}\) B.\(\pi {a^3}\sqrt 3 \) C.\(3\pi {a^3}\) D.\(\pi {a^3}\) Câu 36: Một cốc nước có dạng hình trụ chiều cao là 15cm, đường kính đáy là 6cm, lượng nước ban đầu trong cốc cao 10cm. Thả vào cốc nước 5 viên bị hình cầu có cùng đường kính là 2cm. Hỏi sau khi thả 5 viên bị, mực nước trong cốc cách miệng cốc bao nhiêu cm? (Kết quả làm tròn đến hàng phần trăm). A.4,25cm B.4,26cm C.3,52cm D.4,81cm Câu 37: Cho \(\overrightarrow v \left( {3;3} \right)\)và đường tròn \(\left( C \right):{x^2} + {y^2} - 2x + 4y - 4 = 0\). Ảnh của (C) qua \({T_{\overrightarrow v }}\) là \(\left( {{C'}} \right):\) A.\({\left( {x + 4} \right)^2} + {\left( {y + 1} \right)^2} = 9\) B.\({\left( {x - 4} \right)^2} + {\left( {y - 1} \right)^2} = 4\) C.\({x^2} + {y^2} + 8x + 2y - 4 = 0\) D.\({\left( {x - 4} \right)^2} + {\left( {y - 1} \right)^2} = 9\) Câu 38: Hãy lập phương trình đường thẳng (d) đi qua các điểm cực đại và cực tiểu của đồ thị hàm số \(y = {x^3} + 3m{x^2} - 3x\) A.\(y = mx + 3m - 1\) C.\(y = \left( {2{m^3} - 2} \right)x\) B.\(y = - 2\left( {m + 1} \right)x + m\) D.\(y = - 2x + 2m\) Câu 39: Cho khối chóp S.ABC có \(SA \bot \left( {ABC} \right),\) tam giác ABC vuông tại B, \(AB = a,AC = a\sqrt 3 .\) Tính thể tích khối chóp S.ABC biết rằng \(SB = a\sqrt 5 \) A.\(\dfrac{{{a^3}\sqrt 2 }}{3}\) B. \(\dfrac{{{a^3}\sqrt 6 }}{6}\) C. \(\dfrac{{{a^3}\sqrt 6 }}{4}\) D. \(\dfrac{{{a^3}\sqrt {15} }}{6}\) Câu 40: Bên cạnh con đường trước khi vào thành phố người ta xây một ngọn tháp đèn lộng lẫy. Ngọn tháp hình tứ giác đều S.ABCD cạnh bên SA = 600 mét, \(\widehat {ASB} = {15^ \circ }.\) Do sự cố đường dây điện tại điểm Q (là trung điểm của SA) bị hỏng, người ta tạo ra một con đường từ A đến Q gồm bốn đoạn thẳng: AM, MN, NP, PQ (hình vẽ). Để tiết kiệm kinh phí, kỹ sư đã nghiên cứu và nó được chiều dài con đường từ A đến Q ngắn nhất. Tính tỷ số \(k = \dfrac{{AM + MN}}{{NP + PQ}}.\)
A.\(k = 2\) B.\(k = \dfrac{4}{3}\) C.\(k = \dfrac{3}{2}\) D.\(k = \dfrac{5}{3}.\) Câu 41: Tìm tất cả các giá trị của tham số m để hàm số \(y = {x^3} - 2m{x^2} + {m^2}x + 2\) đạt cực tiểu tại x=1. A.\(m = 3\) B.\(m = 1 \vee m = 3\) C.\(m = - 1\) D.\(m = 1\) Câu 42: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), \(SA = a,AB = a,AC = 2a,\widehat {BAC} = {60^ \circ }\). Tính thể tích khối cầu ngoại tiếp hình chóp S.ABC A.\(V = \dfrac{{20\sqrt 5 \pi {a^3}}}{3}\) B.\(V = \dfrac{{5\sqrt 5 }}{6}\pi {a^3}\) C.\(V = \dfrac{{5\sqrt 5 \pi }}{2}{a^3}\) D.\(V = \dfrac{5}{6}\pi {a^3}\) Câu 43: Cho 3 đồ thị hàm số sau (như hình vẽ). Khẳng định nào sau đây đúng? A.\(a < b < c\) B.\(a < c < b\) C.\(b < a < c\) D.\(b < c < a\)
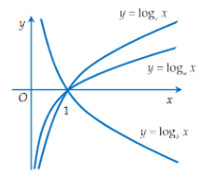
Câu 44: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B với \(AC = a,\) biết SA vuông góc với đáy ABC và SB hợp với đáy một góc \({60^ \circ }\). Tính thể tích hình chóp. A.\(\dfrac{{{a^3}\sqrt 6 }}{{48}}\) B.\(\dfrac{{{a^3}\sqrt 6 }}{{24}}\) C.\(\dfrac{{{a^3}\sqrt 6 }}{8}\) D.\(\dfrac{{{a^3}\sqrt 3 }}{{24}}\) Câu 45: Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số: \(y = 2{\sin ^2}x - \cos x + 1.\) Giá trị \(M + m\) bằng: A.0 B.2 C.\(\dfrac{{25}}{8}\) D.\(\dfrac{{41}}{8}\) Câu 46: Cho hàm số \(y = f(x)\) có đồ thị như hình bên. Xác định tất cả các giá trị của tham số m để phương trình \(\left| {f\left( x \right)} \right| = 2{m^2} - m + 3\) có 6 nghiệm thực phân biệt. A.\( - \dfrac{1}{2} < m < 0\) B.\(0 < m < \dfrac{1}{2}\) C.\(\dfrac{1}{2} < m < 1\) D.\(\left[ \begin{array}{l}\dfrac{1}{2} < m < 1\\ - \dfrac{1}{2} < m < 0\end{array} \right.\)
Câu 47: Tập xác định của hàm số \(y = {\left( {2x - {x^2}} \right)^\pi }\) là: A.\(\left( {0;\dfrac{1}{2}} \right)\) B.\(\left( {0;2} \right)\) C.\(\left( { - \infty ;0} \right) \cup \left( {2; + \infty } \right)\) D.\(\left[ {0;2} \right]\) Câu 48: Có 10 vị nguyên thủ Quốc gia được xếp ngồi vào một dãy ghế dài (Trong đó có ông Trum và ông Kim). Có bao nhiêu cách xếp sao cho hai vị ngày ngồi cạnh nhau? A.\(9!.2\) B.\(10!2\) C.\(8!.2\) D.\(8!\) Câu 49: Tìm tất cả các giá trị của m để hàm số \(y = \dfrac{{m{x^3}}}{3} - m{x^2} + x - 1\) có cực đại và cực tiểu A.\(0 < m \le 1.\) C.\(0 < m < 1.\) B.\(\left[ \begin{array}{l}m < 0\\m > 1\end{array} \right.\) D.\(m < 0.\) Câu 50: Cho hàm số \(y = {x^3} - 3m{x^2} + 6\), giá trị nhỏ nhất của hàm số trên \(\left[ {0;3} \right]\) bằng 2 khi A.\(m = 2\) B.\(m = \dfrac{{31}}{{27}}\) C.\(m > \dfrac{3}{2}\) D.\(m = 1\) Lời giải chi tiết
Xem thêm: Lời giải chi tiết Đề thi thử THPT Quốc gia môn Toán tại HocTot.XYZ HocTot.XYZ
|