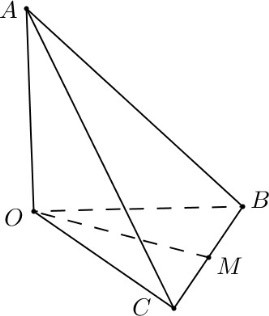
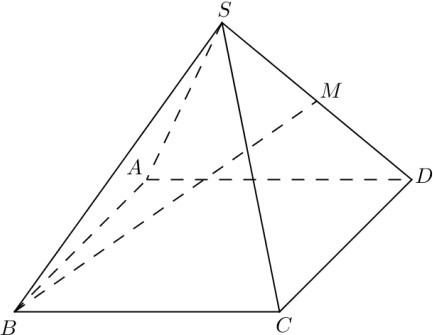
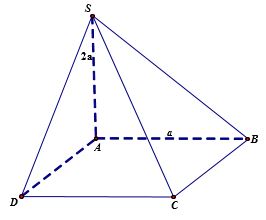
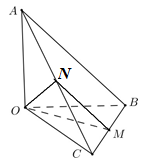
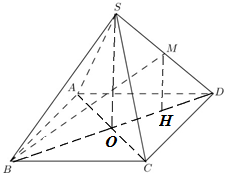
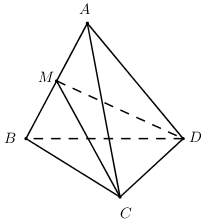
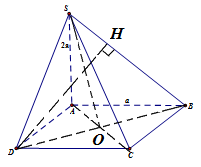
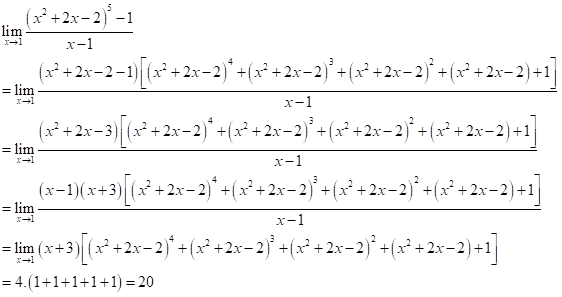Đề số 8 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 11Đáp án và lời giải chi tiết Đề số 8 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán học 11 Đề bài Câu 1: Tính giới hạn \(\mathop {\lim }\limits_{x \to + \infty } \frac{{x + 1}}{{x + 2}}.\) A. \(1.\) B. \(2.\) C. \(3.\) D. \(4\) Câu 2: Tính giới hạn \(\mathop {\lim }\limits_{x \to + \infty } \frac{{x + \sqrt {{x^2} + 1} }}{{x + 2}}.\) A. \(1.\) B. \(2.\) C. \(3.\) D. \(4\) Câu 3: \(\mathop {\lim }\limits_{x \to 1} \frac{{x + \sqrt {{x^2} + 1} }}{{x + 1}} = a + b\sqrt 2 \,\,\left( {a,b \in \mathbb{Q}} \right).\) Tính \(a + b\). A. \(1.\) B. \(2.\) C. \(5.\) D. \(0\) Câu 4: Tính giới hạn \(\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} + x - 2}}{{x - 1}}.\) A. \(1.\) B. \( - 2.\) C. \(3.\) D. \(5\) Câu 5: Tính giới hạn \(\mathop {\lim }\limits_{x \to 2} \left( {x - 2} \right)\). A. \(7.\) B. \( - 2.\) C. \(3.\) D. \(0\) Câu 6: Biết \(\mathop {\lim }\limits_{x \to - \infty } \frac{{x - m\sqrt {{x^2} + 2} }}{{x + 2}} = 2.\)Tìm m. A. \(1.\) B. \( - 2.\) C. \(3.\) D. \(4\) Câu 7: Tìm m để hàm số \(y = \left\{ \begin{array}{l}\frac{{{x^2} - 4}}{{x - 2}}\quad \quad x \ne 2\\m\quad \quad \quad \quad x = 2\end{array} \right.\) liên tục tại \(x = 2?\) A. \(1.\) B. \(2.\) C. \(4.\) D. \( - 4\) Câu 8: Tính giới hạn \(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {2x + 2} - 2x}}{{x - 1}}\). A. \( - \frac{1}{2}.\) B. \(2.\) C. \(3.\) D. \( - \frac{3}{2}.\) Câu 9: Biết \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = m;\,\,\,\mathop {\lim }\limits_{x \to + \infty } g\left( x \right) = n.\) Tính \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) + g(x)} \right]\) A. \(m + n.\) B. \(m - n.\) C. \(m.\) D. \(n\) Câu 10: Biết \(\mathop {\lim }\limits_{x \to 2} f(x) = 3.\)Tính \(\mathop {\lim }\limits_{x \to 2} \left[ {f\left( x \right) + x} \right].\) A. \(5.\) B. \( - 2.\) C. \(1.\) D. \(4\) Câu 11: Tính giới hạn \(\mathop {\lim }\limits_{x \to 1} \frac{{{{\left( {{x^2} + 2x - 2} \right)}^5} - 1}}{{x - 1}}.\) A. \(1.\) B. \(2.\) C. \(3.\) D. \(20\) Câu 12: Tính giới hạn \(\mathop {\lim }\limits_{} \frac{{n + 1}}{{{n^2} + 2}}.\) A. \(1.\) B. \(2.\) C. \(3.\) D. \(0\) Câu 13: Tính giới hạn \(\mathop {\lim }\limits_{} \frac{{n + \sqrt {{n^2} + 1} }}{{n + 3}}.\) A. \(1.\) B. \(2.\) C. \(3.\) D. \(4\) Câu 14: Cho dãy số \({u_n}\) thỏa \(\mathop {\lim }\limits_{} {u_n} = 2.\) Tính \(\mathop {\lim }\limits_{} \left( {{u_n} + \frac{{{2^n}}}{{{2^n} + 3}}} \right).\) A. \(1.\) B. \(2.\) C. \(3.\) D. \(4\) Câu 15: Cho dãy số \({u_n},{v_n}\) thỏa \(\mathop {\lim }\limits_{} {u_n} = 2;\,\,\mathop {\lim }\limits_{} {v_n} = 1.\)Tính \(\mathop {\lim }\limits_{} \left( {2{u_n} - 3{v_n}} \right).\) A. \(1.\) B. \(2.\) C. \(3.\) D. \(7\) Câu 16: Tính đạo hàm của hàm số\(y = {x^2} + 1\). A. \(y' = {x^2} + 1\) B. \(y' = 2x + 1\) C. \(y' = 2x\) D. \(y' = 2x - 1\) Câu 17: Tính đạo hàm của hàm số\(y = \sin 2x\). A. \(y' = 2\sin x\) B. \(y' = \sin 2x\) C. \(y' = 2\cos x\) D. \(y' = 2\cos 2x\) Câu 18: Tính đạo hàm của hàm số \(y = {\left( {{x^2} + x} \right)^2}\). A. \(y' = 3{\left( {{x^2} + x} \right)^2}\) B. \(y' = 2x + 1\) C. \(y' = 2\left( {2x + 1} \right)\) D. \(y' = 2\left( {{x^2} + x} \right)\left( {2x + 1} \right)\) Câu 19: Cho hàm số \(y = f\left( x \right) = {x^2} + mx\) (m là tham số). Tìm m, biết \(f'\left( 1 \right) = 3\). A. \(m = 1.\) B. \(m = 2.\) C. \(m = 3.\) D. \(m = 7\) Câu 20: Cho hàm số \(y = \sin x\).Tính \(y''\left( 0 \right).\) A. \(y''\left( 0 \right) = 0.\) B. \(y''\left( 0 \right) = 1.\) C. \(y''\left( 0 \right) = 2.\) D. \(y''\left( 0 \right) = - 2.\) Câu 21: Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên tập số thực. Tìm hệ thức đúng? A. \(f'\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}}.\) B. \(f'\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right)}}{{x - 1}}.\) C. \(f'\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right)}}{x}.\) D. \(f'\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} \frac{{f\left( 1 \right)}}{{x - 1}}.\) Câu 22: Cho hàm số \(y = f\left( x \right)\) có đạo hàm đến cấp 2 trên tập số thực. Tìm hệ thức đúng? A. \(f''\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}}.\) B. \(f''\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} \frac{{f'\left( x \right) - f'\left( 1 \right)}}{{x - 1}}.\) C. \(f''\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right)}}{x}.\) D. \(f''\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} \frac{{f\left( 1 \right)}}{{x - 1}}.\) Câu 23: Tìm hệ số của x trong khai triển \({\left( {{x^2} + x + 2} \right)^2}\left( {x + 1} \right)\) thành đa thức: A. \(16.\) B. \(6.\) C. \(8.\) D. \(2\) Câu 24: Tìm hệ số của \({x^2}\) trong khai triển \({\left( {{x^2} + x + 2} \right)^3}\) thành đa thức: A. \(12.\) B. \(18.\) C. \(19.\) D. \(20\) Câu 25: Hàm số \(y = \left( {1 + x} \right)\sqrt {1 - x} \)có đạo hàm \(y' = \frac{{ax + b}}{{2\sqrt {1 - x} }}\). Tính \(a + b.\) A. \( - 2.\) B. \(2.\) C. \( - 3.\) D. \(1\) Câu 26: Lập phương trình tiếp tuyến của đồ thị hàm số \(y = {x^2} + 3x + 1\) tại điểm có hoành độ bằng 1. A. \(y = 5x\) B. \(y = 5x + 5\) C. \(y = 5x - 5\) D. \(y = x\) Câu 27: Hàm số \(y = \frac{{\sqrt {{x^2} + 2x + 3} }}{x}\) có đạo hàm \(y' = \frac{{ax + b}}{{{x^2}\sqrt {{x^2} + 2x + 3} }}\). Tìm \(\max \left\{ {a,b} \right\}.\) A. \(2.\) B. \( - 1.\) C. \( - 3.\) D. \( - 7\) Câu 28: Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên tập số thực, biết \(f\left( {3 - x} \right) = {x^2} + x\). Tính \(f'\left( 2 \right)\). A. \(f'\left( 2 \right) = - 1.\) B. \(f'\left( 2 \right) = - 3.\) C. \(f'\left( 2 \right) = - 2.\) D. \(f'\left( 2 \right) = 3.\) Câu 29: Tìm vi phân của hàm số \(y = {x^3}\). A. \(dy = {x^2}dx\) B. \(dy = 3xdx\) C. \(dy = 3{x^2}dx\) D. \(dy = - 3{x^2}dx\) Câu 30: Giải phương trình \(f''\left( x \right) = 0\), biết \(f\left( x \right) = {x^3} - 3{x^2}\). A. \(x = 0\) B. \(x = 2\) C. \(x = 0,\,\,x = 2\) D. \(x = 1\) Câu 31: Cho chuyển động thẳng xác định bởi phương trình \(s = {t^3} - 3{t^2} - 9t + 2\) (t được tính bằng giây, s được tính bằng mét). Tìm gia tốc khi \(t = 2s\). A. \(a = 12m/{s^2}.\) B. \(a = 6m/{s^2}.\) C. \(a = - 9m/{s^2}.\) D. \(a = 2m/{s^2}\) Câu 32: Tìm hệ số góc \(k\) của tiếp tuyến của đồ thị \(y = {x^3} - 2{x^2} - 3x + 1\) tại điểm có hoành độ bằng 0. A. \(k = - 3\) B. \(k = 2\) C. \(k = 1\) D. \(k = 0\). Câu 33: Cho chuyển động thẳng xác định bởi phương trình \(s = {t^2} - 2t + 2\)( t được tính bằng giây, s được tính bằng mét). Tính vận tốc tại thời điểm \(t = 3s\). A. \(v = 2m/s.\) B. \(v = 4m/s.\) C. \(v = - 2m/s.\) D. \(v = - 4m/s.\) Câu 34: Tính \(d\left( {\sin x - x\cos x} \right)\). A. \(d\left( {\sin x - x\cos x} \right) = x\sin xdx\) B. \(d\left( {\sin x - x\cos x} \right) = x\cos xdx\) C. \(d\left( {\sin x - x\cos x} \right) = \cos xdx\) D. \(d\left( {\sin x - x\cos x} \right) = \sin xdx\) Câu 35: Cho tứ diện \(OABC\) có \(OA,\,\,OB,\,\,OC\) đôi một vuông góc với nhau và \(OA = OB = OC = 1\). Gọi \(M\) là trung điểm của \(BC\) (tham khảo hình vẽ bên). Góc giữa hai đường thẳng \(OM\) và \(AB\) bằng:
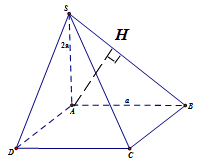
A. \({90^0}\) B. \({30^0}\) C. \({60^0}\) D. \({45^0}\) Câu 36: Cho hình chóp tứ giác đều \(S.ABCD\) có tất cả các cạnh bằng \(a\). Gọi \(M\) là trung điểm của \(SD\) (tham khảo hình vẽ bên). Tang của góc giữa đường thẳng \(BM\) và mặt phẳng \(\left( {ABCD} \right)\) bằng:
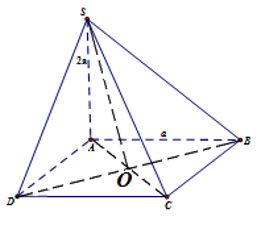
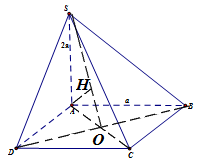
A. \(\frac{2}{3}.\) B. \(\frac{1}{3}.\) C. \(\frac{{\sqrt 3 }}{2}.\) D.\(\frac{{\sqrt 2 }}{2}.\) Câu 37: Cho tứ diện đều ABCD. Tìm góc giữa hai đường thẳng AB và CD. A. \({30^0}.\) B. \({45^0}\) C. \({60^0}\) D. \({90^0}\) Câu 38: Giải bất phương trình \(f'\left( x \right) > 0\), biết \(f\left( x \right) = 2x + \sqrt {1 - {x^2}} .\) A. \(x \in \left( { - 1;\frac{1}{{\sqrt 2 }}} \right).\) B. \(x \in \left( { - 1;1} \right).\) C. \(x \in \left( { - 1;\frac{2}{{\sqrt 5 }}} \right).\) D. \(x \in \left( { - \frac{2}{{\sqrt 5 }};\frac{2}{{\sqrt 5 }}} \right).\) (Đề toán này áp dụng từ câu 39 đến câu 50) Cho hình chóp \(S.ABCD\), đáy \(ABCD\) là hình vuông cạnh \(a\). Đường thẳng \(SA\) vuông góc với mặt phẳng chứa đáy \(\left( {ABCD} \right)\), độ dài cạnh \(SA\) bằng \(2a\) (Tham khảo hình vẽ bên). Câu 39: Đường thẳng nào dưới đây vuông góc với mặt phẳng \(\left( {ABCD} \right)\)? A. \(SD\) B. \(SA\) C. \(SB\) D. \(SC\) Câu 40: Đường thẳng nào dưới đây vuông góc với mặt phẳng \(\left( {SAB} \right)\)? A. \(AB\) B. \(AC\) C. \(AD\) D. \(AS\) Câu 41: Mặt phẳng nào dưới đây vuông góc với mặt phẳng \(\left( {SAB} \right)\)? A.\(\left( {SAB} \right)\) B. \(\left( {SAC} \right)\) C. \(\left( {SAD} \right)\) D.\(\left( {SCD} \right)\) Câu 42: Khoảng cách từ \(S\) đến mặt phẳng \(\left( {ABCD} \right)\)bằng: A. \(SD\) B. \(SA\) C. \(SB\) D. \(SC\) Câu 43: Tính tang của góc tạo bởi hai đường thẳng \(SB\) và \(CD\). A. \(3\) B. \(\sqrt 2 \) C. \(\frac{{\sqrt 2 }}{3}.\) D. \(2\) Câu 44: Tính tang của góc tạo bởi đường thẳng \(SC\) và mặt phẳng \(\left( {ABCD} \right)\). A. \(3\) B. \(\sqrt 2 \) C. \(\frac{{\sqrt 2 }}{3}.\) D. \(2\) Câu 45: Tính khoảng cách giữa hai đường thẳng \(SA\) và \(BC\). A.\(a.\) B. \(\sqrt 2 a\) C. \(2a\) D. \(3a\) Câu 46: Tính côsin của góc tạo bởi mặt phẳng \(\left( {SBD} \right)\) và mặt phẳng \(\left( {ABCD} \right)\). A.\(\frac{1}{3}.\) B. \(3.\) C. \(\sqrt 2 .\) D. \(\frac{3}{{\sqrt 2 }}.\) Câu 47: Tính khoảng cách từ điểm D đến đường thẳng SB. A.\(3a.\) B. \(\frac{3}{5}a.\) C. \(\frac{{3\sqrt 5 }}{5}a.\) D. \(\frac{{\sqrt {21} a}}{3}.\) Câu 48: Biết \(\overrightarrow {AC} = m\overrightarrow {AB} + n\overrightarrow {AD} + p\overrightarrow {AS} \). Tính tổng \(m + n + p\) A.\(3.\) B. \(2.\) C. \(1.\) D. \(0\) Câu 49: Tính khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SBC} \right)\). A.\(a.\) B. \(\sqrt 2 a.\) C. \(\frac{{2\sqrt 5 }}{5}a.\) D. \(\frac{{\sqrt {21} }}{3}a.\) Câu 50: Tính khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SBD} \right)\). A.\(2a.\) B. \(\sqrt 2 a.\) C. \(\frac{2}{3}a.\) D. \(\frac{3}{2}a.\) Lời giải chi tiết
Câu 1 (NB): Phương pháp: Chia cả tử và mẫu cho \(x\). Cách giải: \(\mathop {\lim }\limits_{x \to + \infty } \frac{{x + 1}}{{x + 2}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{1 + \frac{1}{x}}}{{1 + \frac{2}{x}}} = \frac{1}{1} = 1\). Chọn A. Câu 2 (NB): Phương pháp: Chia cả tử và mẫu cho \(x\). Cách giải: \(\begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } \frac{{x + \sqrt {{x^2} + 1} }}{{x + 2}}\\ = \mathop {\lim }\limits_{x \to + \infty } \frac{{1 + \sqrt {1 + \frac{1}{{{x^2}}}} }}{{1 + \frac{2}{x}}}\\ = \frac{{1 + 1}}{1} = 2\end{array}\). Chọn B. Câu 3 (TH): Phương pháp: Hàm số \(y = f\left( x \right)\) liên tục tại \(x = {x_0} \Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\). Cách giải: Hàm số \(y = \frac{{x + \sqrt {{x^2} + 1} }}{{x + 1}}\) có TXĐ: \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\) \( \Rightarrow \) Hàm số liên tục tại \(x = 1\). \(\begin{array}{l} \Rightarrow \mathop {\lim }\limits_{x \to 1} \frac{{x + \sqrt {{x^2} + 1} }}{{x + 1}}\\ = \frac{{1 + \sqrt {{1^2} + 1} }}{{1 + 1}}\\ = \frac{{1 + \sqrt 2 }}{2} = \frac{1}{2} + \frac{1}{2}\sqrt 2 \\ \Rightarrow \left\{ \begin{array}{l}a = \frac{1}{2}\\b = \frac{1}{2}\end{array} \right.\\ \Rightarrow a + b = \frac{1}{2} + \frac{1}{2} = 1\end{array}\) Chọn A. Câu 4 (TH): Phương pháp: Phân tích, rút gọn, khử dạng \(\frac{0}{0}\). Cách giải: \(\begin{array}{l}\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} + x - 2}}{{x - 1}}\\ = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {x - 1} \right)\left( {x + 2} \right)}}{{x - 1}}\\ = \mathop {\lim }\limits_{x \to 1} \left( {x + 2} \right) = 3\end{array}\). Chọn C. Câu 5 (NB): Phương pháp: Hàm số \(y = f\left( x \right)\) liên tục tại \(x = {x_0}\)\( \Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\). Cách giải: \(\mathop {\lim }\limits_{x \to 2} \left( {x - 2} \right) = 2 - 2 = 0\). Chọn D. Câu 6 (TH): Phương pháp: Chia cả tử và mẫu cho \(x\). Cách giải: \(\begin{array}{l}\mathop {\lim }\limits_{x \to - \infty } \frac{{x - m\sqrt {{x^2} + 2} }}{{x + 2}} = 2\\ \Leftrightarrow \mathop {\lim }\limits_{x \to - \infty } \frac{{1 + m\sqrt {1 + \frac{2}{{{x^2}}}} }}{{1 + \frac{2}{x}}} = 2\\ \Leftrightarrow 1 + m = 2 \Leftrightarrow m = 1\end{array}\) Chọn A. Câu 7 (TH): Phương pháp: Hàm số \(y = f\left( x \right)\) liên tục tại \(x = {x_0}\)\( \Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\) Cách giải: Ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to 2} y = \mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 4}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \left( {x + 2} \right) = 4\\y\left( 2 \right) = m\end{array} \right.\) Hàm số liên tục tại \(x = 2\)\( \Leftrightarrow \mathop {\lim }\limits_{x \to 2} y = y\left( 2 \right) \Leftrightarrow m = 4\). Chọn C. Câu 8 (VD): Phương pháp: Sử dụng phương pháp nhân với biểu thức liên hợp đểkhử dạng \(\frac{0}{0}\). Cách giải: \(\begin{array}{l}\,\,\,\,\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {2x + 2} - 2x}}{{x - 1}}\\ = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {\sqrt {2x + 2} - 2x} \right)\left( {\sqrt {2x + 2} + 2x} \right)}}{{\left( {x - 1} \right)\left( {\sqrt {2x + 2} + 2x} \right)}}\\ = \mathop {\lim }\limits_{x \to 1} \frac{{2x + 2 - 4{x^2}}}{{\left( {x - 1} \right)\left( {\sqrt {2x + 2} + 2x} \right)}}\\ = \mathop {\lim }\limits_{x \to 1} \frac{{ - 2\left( {x - 1} \right)\left( {2x + 1} \right)}}{{\left( {x - 1} \right)\left( {\sqrt {2x + 2} + 2x} \right)}}\\ = \mathop {\lim }\limits_{x \to 1} \frac{{ - 2\left( {2x + 1} \right)}}{{\sqrt {2x + 2} + 2x}}\\ = \frac{{ - 2.\left( {2.1 + 1} \right)}}{{\sqrt {2.1 + 2} + 2.1}} = - \frac{3}{2}\end{array}\) Chọn D. Câu 9 (TH): Phương pháp: \(\mathop {\lim }\limits_{x \to \infty } \left[ {f\left( x \right) + g\left( x \right)} \right]\)\( = \mathop {\lim }\limits_{x \to \infty } f\left( x \right) + \mathop {\lim }\limits_{x \to \infty } g\left( x \right)\) . Cách giải: \(\begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) + g\left( x \right)} \right]\\ = \mathop {\lim }\limits_{x \to + \infty } f\left( x \right) + \mathop {\lim }\limits_{x \to + \infty } g\left( x \right)\\ = m + n\end{array}\). Chọn A. Câu 10 (TH): Phương pháp: \(\mathop {\lim }\limits_{x \to \infty } \left[ {f\left( x \right) + g\left( x \right)} \right]\)\( = \mathop {\lim }\limits_{x \to \infty } f\left( x \right) + \mathop {\lim }\limits_{x \to \infty } g\left( x \right)\). Cách giải: \(\begin{array}{l}\mathop {\lim }\limits_{x \to 2} \left[ {f\left( x \right) + x} \right]\\ = \mathop {\lim }\limits_{x \to 2} f\left( x \right) + \mathop {\lim }\limits_{x \to 2} x\\ = 3 + 2 = 5\end{array}\). Chọn A. Câu 11 (VD): Phương pháp: Phân tích, rút gọn, khử dạng \(\frac{0}{0}\). Cách giải:
Chọn D. Câu 12 (NB): Phương pháp: Chia cả tử và mẫu cho \({n^2}\). Cách giải: \(\mathop {\lim }\limits_{} \frac{{n + 1}}{{{n^2} + 2}} = \lim \frac{{\frac{1}{n} + \frac{1}{{{n^2}}}}}{{1 + \frac{2}{{{n^2}}}}} = 0\). Chọn D. Câu 13 (TH): Phương pháp: Chia cả tử và mẫu cho \(n\). Cách giải: \(\begin{array}{l}\lim \frac{{n + \sqrt {{n^2} + 1} }}{{n + 3}}\\ = \lim \frac{{1 + \sqrt {1 + \frac{1}{{{n^2}}}} }}{{1 + \frac{3}{n}}}\\ = \frac{{1 + 1}}{1} = 2\end{array}\) Chọn B. Câu 14 (VD): Phương pháp: \(\mathop {\lim }\limits_{x \to \infty } \left[ {f\left( x \right) + g\left( x \right)} \right]\)\( = \mathop {\lim }\limits_{x \to \infty } f\left( x \right) + \mathop {\lim }\limits_{x \to \infty } g\left( x \right)\). Cách giải: \(\begin{array}{l}\lim \left( {{u_n} + \frac{{{2^n}}}{{{2^n} + 3}}} \right)\\ = \lim {u_n} + \lim \frac{{{2^n}}}{{{2^n} + 3}}\\ = \lim {u_n} + \lim \frac{1}{{1 + \frac{3}{{{2^n}}}}}\\ = 2 + 1 = 3\end{array}\). Chọn C. Câu 15 (TH): Phương pháp: \(\mathop {\lim }\limits_{x \to \infty } \left[ {f\left( x \right) - g\left( x \right)} \right]\)\( = \mathop {\lim }\limits_{x \to \infty } f\left( x \right) - \mathop {\lim }\limits_{x \to \infty } g\left( x \right)\) Cách giải: \(\begin{array}{l}\lim \left( {2{u_n} - 3{v_n}} \right)\\ = 2\lim {u_n} - 3\lim {v_n}\\ = 2.2 - 3.1 = 1\end{array}\). Chọn A. Câu 16 (NB): Phương pháp: Sử dụng công thức \(\left( {{x^n}} \right)' = n{x^{n - 1}}\,\,\left( {x \ne - 1} \right)\). Cách giải: \(y = {x^2} + 1 \Rightarrow y' = 2x\). Chọn C. Câu 17 (TH): Phương pháp: Sử dụng công thức \(\left( {\sin kx} \right)' = k\cos kx\). Cách giải: \(y = \sin 2x \Rightarrow y' = 2\cos 2x\). Chọn D. Câu 18 (TH): Phương pháp: Sử dụng công thức \(\left( {{u^n}} \right)' = n{u^{n - 1}}u'\). Cách giải: Ta có: \(y' = 2\left( {{x^2} + x} \right)\left( {2x + 1} \right)\). Chọn D. Câu 19 (TH): Phương pháp: Sử dụng công thức \(\left( {\sin kx} \right)' = k\cos kx\). Cách giải: Ta có: \(f'\left( x \right) = 2x + m\) \( \Rightarrow f'\left( 1 \right) = 2 + m = 3 \Leftrightarrow m = 1\) Chọn A. Câu 20 (TH): Phương pháp: Sử dụng công thức \(\begin{array}{l}\left( {\sin x} \right)' = \cos x\\\left( {\cos x} \right)' = - \sin x\end{array}\). Cách giải: Ta có: \(\begin{array}{l}y' = \left( {\sin x} \right)' = \cos x\\y'' = \left( {\cos x} \right)' = - \sin x\end{array}\). \( \Rightarrow y''\left( 0 \right) = - \sin 0 = 0\). Chọn A. Câu 21 (NB): Cách giải: Hệ thức đúng là: \(f'\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}}.\) Chọn A. Câu 22 (TH): Cách giải: Chọn B. Câu 23 (VDC): Phương pháp: Sử dụng khai triển nhị thức Newton: \({\left( {a + b} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^k}{b^{n - k}}} \). Cách giải: \(\begin{array}{l}{\left( {{x^2} + x + 2} \right)^2}\left( {x + 1} \right)\\ = \left( {x + 1} \right)\sum\limits_{k = 0}^2 {C_2^k{{\left( {{x^2} + x} \right)}^k}{{.2}^{2 - k}}} \\ = \left( {x + 1} \right)\sum\limits_{k = 0}^2 {C_2^k{2^{2 - k}}\sum\limits_{l = 0}^k {C_k^l{{\left( {{x^2}} \right)}^l}{x^{k - l}}} } \\ = \left( {x + 1} \right)\sum\limits_{k = 0}^2 {C_2^k{2^{2 - k}}\sum\limits_{l = 0}^k {C_k^l{x^{k + l}}} } \end{array}\) Số hạng chứa \(x\) trong khai triển trên là: \(C_2^0{2^2}.C_0^0x + C_2^1{.2^1}.C_1^0\). Vậy hệ số của số hạng chứa \(x\) trong khai triển trên là: \(C_2^0{2^2}.C_0^0 + C_2^1{.2^1}.C_1^0 = 8\). Chọn C. Câu 24 (VDC): Phương pháp: Sử dụng khai triển nhị thức Newton: \({\left( {a + b} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^k}{b^{n - k}}} \). Cách giải: \(\begin{array}{l}{\left( {{x^2} + x + 2} \right)^3}\\ = \sum\limits_{k = 0}^3 {C_3^k{{\left( {{x^2}} \right)}^{3 - k}}{{\left( {x + 2} \right)}^k}} \\ = \sum\limits_{k = 0}^3 {C_3^k{x^{6 - 2k}}\sum\limits_{l = 0}^k {C_k^l{x^l}{2^{k - l}}} } \end{array}\). (với \(0 \le k \le 3;\,\,0 \le l \le 3;\,\,k,l \in \mathbb{Z}\)) Hệ số của \({x^2}\) trong khai triển trên ứng với: \(6 - 2k + l = 2\)\( \Leftrightarrow 2k - l = 4\) \( \Leftrightarrow \left[ \begin{array}{l}k = 2;l = 0\\k = 3;l = 2\end{array} \right.\). Vậy hệ số của \({x^2}\) trong khai triển trên là: \(C_3^2C_2^0{2^2} + C_3^3C_3^2{.2^1} = 18\). Chọn B. Câu 25 (TH): Phương pháp: Sử dụng quy tắc tính đạo hàm \(\left( {uv} \right)' = u'v - uv'\). Cách giải: \(\begin{array}{l}y' = \sqrt {1 - x} + \left( {1 + x} \right)\frac{{ - 1}}{{2\sqrt {1 - x} }}\\ = \frac{{2\left( {1 - x} \right) - 1 - x}}{{2\sqrt {1 - x} }} = \frac{{1 - 3x}}{{2\sqrt {1 - x} }}\\ \Rightarrow \left\{ \begin{array}{l}a = - 3\\b = 1\end{array} \right.\\ \Rightarrow a + b = - 3 + 1 = - 2\end{array}\) Chọn A. Câu 26 (TH): Phương pháp: Phương trình tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm có hoành độ \(x = {x_0}\) là: \(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + f\left( {{x_0}} \right)\). Cách giải: Ta có: \(y' = 2x + 3 \Rightarrow y'\left( 1 \right) = 5\) và \(y\left( 1 \right) = 5\). Vậy phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng 1 là: \(y = 5\left( {x - 1} \right) + 5 = 5x\). Chọn A. Câu 27 (VD): Phương pháp: Sử dụng quy tắc tính đạo hàm \(\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{{{v^2}}}\). Cách giải: Ta có: \(\begin{array}{l}y' = \frac{{\frac{{2x + 2}}{{2\sqrt {{x^2} + 2x + 3} }}.x - \sqrt {{x^2} + 2x + 3} }}{{{x^2}}}\\y' = \frac{{{x^2} + x - {x^2} - 2x - 3}}{{{x^2}\sqrt {{x^2} + 2x + 3} }}\\ = \frac{{ - x - 3}}{{{x^2}\sqrt {{x^2} + 2x + 3} }}\\ \Rightarrow \left\{ \begin{array}{l}a = - 1\\b = - 3\end{array} \right.\\ \Rightarrow \max \left\{ {a;b} \right\} = \max \left\{ { - 1; - 3} \right\}\\ = - 1\end{array}\) Chọn B. Câu 28 (VD): Phương pháp: Sử dụng công thức tính đạo hàm hàm hợp: \(\left[ {f\left( u \right)} \right]' = u'.f'\left( u \right)\). Cách giải: \(f\left( {3 - x} \right) = {x^2} + x\)\( \Rightarrow - f'\left( {3 - x} \right) = 2x + 1\) . Thay \(x = 1\) ta có \( - f'\left( 2 \right) = 2.1 + 1 = 3\)\( \Rightarrow f'\left( 2 \right) = - 3\). Chọn B. Câu 29 (NB): Phương pháp: Sử dụng công thức tính vi phân: \(dy = y'dx\). Cách giải: \(dy = d\left( {{x^3}} \right) = \left( {{x^3}} \right)'dx = 3{x^2}dx\). Chọn C. Câu 30 (TH): Phương pháp: Sử dụng công thức \(\left( {{x^n}} \right)' = n{x^{n - 1}}\,\,\left( {x \ne - 1} \right)\). Cách giải: \(\begin{array}{l}f'\left( x \right) = 3{x^2} - 6x \Rightarrow f''\left( x \right) = 6x - 6\\ \Rightarrow f''\left( x \right) = 0 \Leftrightarrow 6x - 6 = 0 \Leftrightarrow x = 1\end{array}\) Chọn D. Câu 31 (TH): Phương pháp: Sử dụng công thức \(a\left( t \right) = s''\left( t \right)\). Cách giải: Ta có: \(s'\left( t \right) = 3{t^2} - 6t - 9\)\( \Rightarrow s''\left( t \right) = 6t - 6\) \(\begin{array}{l} \Rightarrow a\left( t \right) = s''\left( t \right) = 6t - 6\\ \Rightarrow a\left( 2 \right) = 6.2 - 6 = 6\,\,\left( {m/{s^2}} \right)\end{array}\) Chọn B. Câu 32 (TH): Phương pháp: Hệ số góc của tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm có hoành độ \(x = {x_0}\) là \(k = f'\left( {{x_0}} \right)\). Cách giải: Ta có: \(y' = 3{x^2} - 4x - 3\). Hệ số góc của tiếp tuyến của đồ thị hàm số tại điểm có hoành độ \(x = 0\) là \(k = y'\left( 0 \right) = - 3\). Chọn A. Câu 33 (TH): Phương pháp: Sử dụng mối quan hệ: \(v\left( t \right) = s'\left( t \right)\). Cách giải: Ta có: \(v\left( t \right) = s'\left( t \right) = 2t - 2\)\( \Rightarrow v\left( 3 \right) = 2.3 - 2 = 4\,\,\left( {m/s} \right)\) . Chọn B. Câu 34 (TH): Phương pháp: Sử dụng công thức tính vi phân: \(dy = y'dx\). Cách giải: \(\begin{array}{l}d\left( {\sin x - x\cos x} \right)\\ = \left( {\sin x - x\cos x} \right)'dx\\ = \left( {\cos x - \left( {\cos x - x\sin x} \right)} \right)dx\\ = x\sin xdx\end{array}\). Chọn A. Câu 35 (VD): Phương pháp: Gọi \(N\) là trung điểm của \(AC \Rightarrow MN\) là đường trung bình của tam giác \( \Rightarrow MN//AB\)\( \Rightarrow \angle \left( {OM;AB} \right) = \angle \left( {OM;MN} \right)\). Cách giải:
Gọi \(N\) là trung điểm của \(AC \Rightarrow MN\) là đường trung bình của tam giác \( \Rightarrow MN//AB\)\( \Rightarrow \angle \left( {OM;AB} \right) = \angle \left( {OM;MN} \right)\). Trong tam giác vuông \(OBC\) có \(OM = \frac{1}{2}BC = \frac{{\sqrt 2 }}{2}\). Trong tam giác vuông \(OAC\) có \(ON = \frac{1}{2}AC = \frac{{\sqrt 2 }}{2}\). Trong tam giác vuông \(OAB\) có \(MN = \frac{1}{2}AB = \frac{{\sqrt 2 }}{2}\). \( \Rightarrow OM = ON = MN = \frac{{\sqrt 2 }}{2}\) \( \Rightarrow \Delta OMN\) đều \( \Rightarrow \angle OMN = {60^0}\). Vậy \(\angle \left( {OM;AB} \right) = {60^0}\). Chọn C. Câu 36 (VD): Phương pháp: Góc giữa đường thẳng và mặt phẳng cắt nhau là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó. Cách giải:
Gọi \(O = AC \cap BD\). Do chóp \(S.ABCD\) đều \( \Rightarrow SO \bot \left( {ABCD} \right)\). Trong \(\left( {SBD} \right)\) kẻ \(MH//SO\,\,\left( {H \in BD} \right)\)\( \Rightarrow MH \bot \left( {ABCD} \right)\). \( \Rightarrow \angle \left( {BM;\left( {ABCD} \right)} \right)\)\( = \angle \left( {BM;BH} \right) = \angle MBH\). \(ABCD\) là hình vuông cạnh \(a\)\( \Rightarrow AC = BD = a\sqrt 2 \). \( \Rightarrow OB = OD = \frac{1}{2}BD = \frac{{a\sqrt 2 }}{2}\). Dễ thấy \(MH\) là đường trung bình của \(\Delta SOD\) \( \Rightarrow H\) là trung điểm của \(OD\) và \(MH = \frac{1}{2}SO\). \( \Rightarrow BH = \frac{3}{4}BD = \frac{{3a\sqrt 2 }}{4}\) và \(MH = \frac{1}{2}SO = \frac{1}{2}\sqrt {S{D^2} - O{D^2}} \)\( = \frac{1}{2}\sqrt {{a^2} - \frac{{{a^2}}}{2}} = \frac{{a\sqrt 2 }}{4}\). Trong tam giác vuông \(BMH\) có: \(\tan \angle MBH = \frac{{MH}}{{BH}}\)\( = \frac{{\frac{{a\sqrt 2 }}{4}}}{{\frac{{3a\sqrt 2 }}{4}}} = \frac{1}{3}\). Vậy \(\tan \angle \left( {BM;\left( {ABCD} \right)} \right) = \frac{1}{3}\). Chọn B. Câu 37 (TH): Phương pháp: Gọi \(M\) là trung điểm của \(AB\). Chứng minh \(AB \bot \left( {CDM} \right)\). Cách giải:
Gọi \(M\) là trung điểm của \(AB\). \(\Delta ABC,\,\,\Delta ABD\) là các tam giác đều \( \Rightarrow CM \bot AB;\,\,DM \bot AB\)\( \Rightarrow AB \bot \left( {CDM} \right)\). Mà \(CD \subset \left( {CDM} \right) \Rightarrow AB \bot CD\). Vậy \(\angle \left( {AB;CD} \right) = {90^0}\). Chọn D. Câu 38 (VD): Phương pháp: +) Tính \(f'\left( x \right)\). +) Giải BPT dạng \(\sqrt {f\left( x \right)} > g\left( x \right)\) \( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}f\left( x \right) \ge 0\\g\left( x \right) < 0\end{array} \right.\\\left\{ \begin{array}{l}g\left( x \right) \ge 0\\f\left( x \right) > {g^2}\left( x \right)\end{array} \right.\end{array} \right.\) Cách giải: \(\begin{array}{l}DKXD:\,\, - 1 \le x \le 1\\f'\left( x \right) = 2 + \frac{{ - 2x}}{{2\sqrt {1 - {x^2}} }}\\ = 2 - \frac{x}{{\sqrt {1 - {x^2}} }}\\f'\left( x \right) > 0\\ \Leftrightarrow 2 - \frac{x}{{\sqrt {1 - {x^2}} }} > 0\\ \Leftrightarrow \frac{{2\sqrt {1 - {x^2}} - x}}{{\sqrt {1 - {x^2}} }} > 0\,\,\left( {x \in \left( { - 1;1} \right)} \right)\\ \Leftrightarrow 2\sqrt {1 - {x^2}} - x > 0\\ \Leftrightarrow 2\sqrt {1 - {x^2}} > x\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}1 - {x^2} > 0\\x < 0\end{array} \right.\\\left\{ \begin{array}{l}x \ge 0\\4\left( {1 - {x^2}} \right) > {x^2}\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l} - 1 < x < 1\\x < 0\end{array} \right.\\\left\{ \begin{array}{l}x \ge 0\\5{x^2} < 4\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} - 1 < x < 0\\\left\{ \begin{array}{l}x \ge 0\\\frac{{ - 2}}{{\sqrt 5 }} < x < \frac{2}{{\sqrt 5 }}\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} - 1 < x < 0\\0 \le x < \frac{2}{{\sqrt 5 }}\end{array} \right.\\ \Leftrightarrow - 1 < x < \frac{2}{{\sqrt 5 }}\,\,\left( {tm} \right)\end{array}\) Vậy nghiệm của BPT là: \(x \in \left( { - 1;\frac{2}{{\sqrt 5 }}} \right).\) Chọn C. Câu 39 (NB): Cách giải: \(SA \bot \left( {ABCD} \right)\,\,\left( {gt} \right)\) Chọn B. Câu 40 (TH): Phương pháp: \(\left\{ \begin{array}{l}d \bot a\\d \bot b\\a \cap b \subset \left( P \right)\end{array} \right. \Rightarrow d \bot \left( P \right)\). Cách giải: Ta có \(\left\{ \begin{array}{l}AD \bot AB\\AD \bot SA\end{array} \right. \Rightarrow AD \bot \left( {SAB} \right)\). Chọn C. Câu 41 (TH): Phương pháp: \(\left\{ \begin{array}{l}d \bot \left( P \right)\\d \subset \left( Q \right)\end{array} \right. \Rightarrow \left( P \right) \bot \left( Q \right)\). Cách giải: Ta có \(\left\{ \begin{array}{l}AD \bot AB\\AD \bot SA\end{array} \right. \Rightarrow AD \bot \left( {SAB} \right)\). Mà \(AD \subset \left( {SAD} \right)\)\( \Rightarrow \left( {SAB} \right) \bot \left( {SAD} \right)\). Chọn C. Câu 42 (NB): Phương pháp: Khoảng cách từ \(S\) đến \(\left( {ABCD} \right)\) bằng độ dài khoảng cách từ \(S\) đến hình chiếu của \(S\) lên \(\left( {ABCD} \right)\). Cách giải: \(SA \bot \left( {ABCD} \right)\)\( \Rightarrow d\left( {S;\left( {ABCD} \right)} \right) = SA\). Chọn B. Câu 43 (TH): Phương pháp: Ta có: \(CD//AB\) \( \Rightarrow \angle \left( {SB;CD} \right)\) \( = \angle \left( {SB;AB} \right) = \angle SBA\) Cách giải: Ta có \(CD//AB\) \( \Rightarrow \angle \left( {SB;CD} \right)\) \( = \angle \left( {SB;AB} \right) = \angle SBA\) \(\tan \angle SBA = \frac{{SA}}{{AB}} = \frac{{2a}}{a} = 2\) Vậy \(\tan \angle \left( {SB;CD} \right) = 2\). Chọn D. Câu 44 (VD): Phương pháp: Góc giữa đường thẳng và mặt phẳng cắt nhau là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó. Cách giải: Ta có \(SA \bot \left( {ABCD} \right)\) \( \Rightarrow \angle \left( {SC;\left( {ABCD} \right)} \right)\) \( = \angle \left( {SC;AC} \right) = \angle SCA\) \(ABCD\) là hình vuông cạnh \(a \Rightarrow AC = a\sqrt 2 \). \( \Rightarrow \tan \angle SCA = \frac{{SA}}{{AC}} = \frac{{2a}}{{a\sqrt 2 }} = \sqrt 2 \). Chọn B. Câu 45 (TH): Phương pháp: \(BC//AD \Rightarrow BC//\left( {SAD} \right)\) \( \Rightarrow d\left( {SA;BC} \right) = d\left( {B;\left( {SAD} \right)} \right)\) Cách giải: Ta có \(BC//AD \Rightarrow BC//\left( {SAD} \right)\) \( \Rightarrow d\left( {SA;BC} \right) = d\left( {B;\left( {SAD} \right)} \right)\) Ta có \(\left\{ \begin{array}{l}AB \bot AD\\AB \bot SA\end{array} \right. \Rightarrow AB \bot \left( {SAD} \right)\) \( \Rightarrow d\left( {B;\left( {SAD} \right)} \right) = AB = a\) Vậy \(d\left( {SA;BC} \right) = a\). Chọn A. Câu 46 (VD): Phương pháp: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và vuông góc với giao tuyến. Cách giải: Gọi \(O = AC \cap BD\) ta có: \(\left\{ \begin{array}{l}BD \bot AO\\BD \bot SA\end{array} \right.\)\( \Rightarrow BD \bot \left( {SAO} \right) \Rightarrow BD \bot SO\). \(\begin{array}{l}\left\{ \begin{array}{l}\left( {SBD} \right) \cap \left( {ABCD} \right) = BD\\\left( {SBD} \right) \supset SO \bot BD\\\left( {ABCD} \right) \supset AO \bot BD\end{array} \right.\\ \Rightarrow \angle \left( {\left( {SBD} \right);\left( {ABCD} \right)} \right)\\ = \angle \left( {SO;AO} \right) = \angle SOA\end{array}\) \(ABCD\) là hình vuông cạnh \(a\)\( \Rightarrow AO = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\). Trong tam giác vuông \(SAO:\) \(SO = \sqrt {S{A^2} + O{A^2}} \) \( = \sqrt {4{a^2} + \frac{{{a^2}}}{2}} = \frac{{3a}}{{\sqrt 2 }}\) Vậy \(\cos \angle SOA = \frac{{AO}}{{SO}}\)\( = \frac{{\frac{{a\sqrt 2 }}{2}}}{{\frac{{3a}}{{\sqrt 2 }}}} = \frac{1}{3}\). Chọn A. Câu 47 (VD): Phương pháp: Kẻ \(DH \bot SB\,\,\left( {H \in SB} \right)\)\( \Rightarrow d\left( {D;SB} \right) = DH\). Cách giải:
Gọi \(O = AC \cap BD\) \( \Rightarrow OB = OD = \frac{1}{2}BD = \frac{{a\sqrt 2 }}{2}\). Ta có \(SB = SD = \sqrt {4{a^2} + {a^2}} = a\sqrt 5 \) \( \Rightarrow \Delta SBD\) cân tại \(S \Rightarrow SO \bot BD\). \( \Rightarrow SO = \sqrt {S{B^2} - O{B^2}} \)\( = \sqrt {5{a^2} - \frac{{{a^2}}}{2}} = \frac{{3a}}{{\sqrt 2 }}\). Trong tam giác vuông \(SOB:\) \(\tan \widehat {SBO} = \frac{{SO}}{{OB}} = \frac{{\frac{{3a}}{{\sqrt 2 }}}}{{\frac{a}{{\sqrt 2 }}}} = 3\). \(\begin{array}{l} \Rightarrow \cos \widehat {SBO} = \sqrt {\frac{1}{{1 + {{\tan }^2}\widehat {SBO}}}} \\ = \frac{1}{{\sqrt {1 + {3^2}} }} = \frac{1}{{\sqrt {10} }}\\ \Rightarrow \sin \widehat {SBO} = \frac{3}{{\sqrt {10} }}\end{array}\). Kẻ \(DH \bot SB\,\,\left( {H \in SB} \right)\)\( \Rightarrow d\left( {D;SB} \right) = DH\). Trong \({\Delta _v}BDH\) có: \(DH = BD.\sin \widehat {SBO}\)\( = a\sqrt 2 .\frac{3}{{\sqrt {10} }} = \frac{{3\sqrt 5 }}{5}a\). Chọn C. Câu 48 (TH): Phương pháp: Áp dụng quy tắc hình hình hành. Cách giải: Ta có \(ABCD\) là hình vuông \( \Rightarrow \overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \) \(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}m = 1\\n = 1\\p = 0\end{array} \right.\\ \Rightarrow m + n + p = 1 + 1 + 0 = 2\end{array}\) Chọn B. Câu 49 (VD): Phương pháp: Trong \(\left( {SAB} \right)\) kẻ \(AH \bot SB\,\,\left( {H \in SB} \right)\), chứng minh \(d\left( {A;\left( {SBC} \right)} \right) = AH\). Cách giải:
Trong \(\left( {SAB} \right)\) kẻ \(AH \bot SB\,\,\left( {H \in SB} \right)\) ta có \(\begin{array}{l}\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right)\\ \Rightarrow BC \bot AH\\\left\{ \begin{array}{l}AH \bot BC\,\,\left( {cmt} \right)\\AH \bot SB\end{array} \right.\\ \Rightarrow AH \bot \left( {SBC} \right)\\ \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = AH\end{array}\) Áp dụng hệ thức lượng trong tam giác vuông \(SAB\) ta có: \(AH = \frac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }}\)\( = \frac{{2a.a}}{{\sqrt {4{a^2} + {a^2}} }} = \frac{{2a\sqrt 5 }}{5}\) Chọn C. Câu 50 (VD): Cách giải:
Gọi \(O = AC \cap BD\) ta có: \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)\). Trong \(\left( {SAC} \right)\) kẻ \(AH \bot SO\,\,\left( {H \in SO} \right)\)\( \Rightarrow BD \bot AH\). \( \Rightarrow AH \bot \left( {SBD} \right)\)\( \Rightarrow d\left( {A;\left( {SBD} \right)} \right) = AH\). \(ABCD\) là hình vuông cạnh \(a\)\( \Rightarrow AC = a\sqrt 2 \) \( \Rightarrow AO = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\). Áp dụng hệ thức lượng trong tam giác vuông \(SAO\) ta có : \(AH = \frac{{SA.AO}}{{\sqrt {S{A^2} + A{O^2}} }}\)\( = \frac{{2a.\frac{{a\sqrt 2 }}{2}}}{{\sqrt {4{a^2} + \frac{{{a^2}}}{2}} }} = \frac{{2a}}{3}\). Chọn C. HocTot.XYZ
|