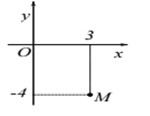
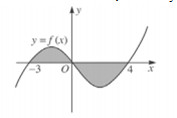
Đề số 8 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 12Đáp án và lời giải chi tiết Đề số 8 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán học 12 Đề bài PHẦN I. TRẮC NGHIỆM (6 điểm) Câu 1:Cho số phức z = 3 – 2i. Tìm điểm biểu diễn của số phức \({\rm{w}} = z + i.\overline z \) A. M(5;-5). B. M(1;-5). C. M(1;1). D. M(5;1). Câu 2: Họ nguyên hàm của hàm số f(x) = cos3x là: A.\( - \dfrac{1}{3}\sin 3x + C.\) B.\(\dfrac{1}{3}\sin 3x + C.\) C.\(3\sin 3x + C.\) D.\( - 3\sin 3x + C.\) Câu 3: Biết \(\int\limits_0^2 {{e^{3x}}} dx = \dfrac{{{e^a} - 1}}{b}.\) Tìm khẳng địng đúng trong các khẳng định sau? A. a + b = 10. B. a = b. C. a = 2b. D. a < b. Câu 4: Công thức nguyên hàm nào sau đây không đúng? A.\(\int {\dfrac{1}{{{{\cos }^2}x}}} = {\mathop{\rm t}\nolimits} + C.\) B.\(\int {{a^x}dx} = \dfrac{{{a^x}}}{{\ln a}} + C(0 < a \ne 1).\) C.\(\int {{x^\alpha }} = \dfrac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C(\alpha \ne - 1).\) D.\(\int {\dfrac{1}{x}} = \ln x + C.\) Câu 5: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \(d:\dfrac{{x - 1}}{2} = \dfrac{{y + 1}}{{ - 3}} = \dfrac{{z - 5}}{4}\) và mặt phẳng (P); x – 3y + 2z – 5 = 0. Mệnh đề nào sau đây không đúng? A. d cắt và không vuông góc với (P). B.d vuông góc với (P). C. d song song với (P). D. d nằm trong (P). Câu 6: Phương trình tham số của đường thẳng đi qua điểm A(1;4;7) và vuông góc với mặt phẳng (P): x + 3y - 2z – 3 = 0 là: A.\(\left\{ \begin{array}{l}x = 1 + 2t\\y = 4 + 4t\\z = 7 - 4t\end{array} \right.\) B.\(\left\{ \begin{array}{l}x = - 4 + t\\y = 3 + 2t\\z = - 1 - 2t\end{array} \right.\) C.\(\left\{ \begin{array}{l}x = 1 + 4t\\y = 4 + 3t\\z = 7 + t\end{array} \right.\) D.\(\left\{ \begin{array}{l}x = 1 + t\\y = 2 + 4t\\z = - 2 + 7t\end{array} \right.\) Câu 7: Cho A(1;2;3), mặt phẳng (P): x + y + z – 2 = 0. Phương trình mặt phẳng song song với mặt phẳng (P) biết (Q) cách điểm A một khoảng bằng \(3\sqrt 3 \) là: A. x + y + z + 3 = 0 và x + y + z – 3 = 0. B. x + y + z + 3 = 0 và x + y + z + 15 = 0. C. x + y + z + 3 = 0 và x + y + z – 15 = 0. D. x + y + z + 3 = 0 và x + y – z – 15 = 0. Câu 8: Điểm M trong hình vẽ bên là điểm biểu diễn của số phức z. Tìm phần thực và phần ảo của số phức z. A. Phần thực là – 4 và phần ảo là 3. B. Phần thực là 3 và phần ảo là – 4i. C. Phần thực là 3 và phần ảo là – 4. D. Phần thực là – 4 và phần ảo là 3i. Câu 9: Biết \(\int\limits_a^b {f(x)dx = 10} ,F(x)\) là một nguyên hàm của f(x) và F(a) = - 3. Tính F(b). A. F(b) = 13. B. F(b) = 10. C. F(b) = 16. D. F(b) = 7. Câu 10: Tìm số phức liên hợp của số phức z = i(3i+1). A.\(\overline z = 3 - i.\) B.\(\overline z = - 3 - i.\) C.\(\overline z = - 3 + i.\) D.\(\overline z = 3 + i.\) Câu 11: Biết F(x) là một nguyên hàm của hàm số \(f(x) = \dfrac{4}{{1 + 2x}}\) và F(0) = 2. Tìm F(2). A. 4ln5 + 2. B. 5 (1 + ln2). C. 2 ln5 + 4. D. 2 (1+ln5). Câu 12: Diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = {x^2},\) trục hoành và hai đường thẳng x = -1, x = 3 là: A. \(\dfrac{1}{3}.\) B.\(\dfrac{{28}}{3}.\) C.\(\dfrac{8}{3}.\) D.\(\dfrac{{28}}{9}.\) Câu 13: Gọi \({z_1}\) và \({z_2}\) lần lượt là nghiệm của phương trình: \({z^2} - 2z + 5 = 0.\) Tính \(P = \left| {{z_1}} \right| + \left| {{z_2}} \right|.\) A.\(2\sqrt 5 .\) B. 10. C. 3. D. 6. Câu 14: Tính mô đun của số phức z thỏa mãn: z(2 – i) + 13i = 1. A.\(\left| z \right| = \dfrac{{\sqrt {34} }}{3}.\) B.\(\left| z \right| = \dfrac{{5\sqrt {34} }}{2}.\) C.\(\left| z \right| = 34.\) D.\(\left| z \right| = \sqrt {34} .\) Câu 15: Tích phân \(I = \int\limits_0^1 {\dfrac{{2dx}}{{3 - 2x}}} = \ln a.\) Giá trị của a bằng: A. 3. B. 2. C. 4. D.1. Câu 16: Biết \(\int\limits_0^3 {f(x)dx = 12} .\) Tính \(I = \int\limits_0^1 {f(x)dx} .\) A. 4. B. 6. C. 36. D. 3. Câu 17: F(x) là nguyên hàm của hàm số \(f(x) = \dfrac{{3x + 4}}{{{x^2}}},(x \ne 0),\) biết rằng F(1) = 1. F(x) là biểu thức nào sau đây: A.\(F(x) = 2x + \dfrac{4}{x} - 5.\) B.\(F(x) = 3\ln \left| x \right| + \dfrac{4}{x} + 5.\) C.\(F(x) = 3x - \dfrac{4}{x} + 3.\) D.\(F(x) = 3\ln \left| x \right| - \dfrac{4}{x} + 3.\) Câu 18: Trong hệ tọa Oxyz, cho hai điểm A(3;-2;-1), B(4;-1;2). Phương trình mặt phẳng trung trực của đoạn thẳng AB là: A. \(2x + 2y + 3z + 1 = 0. \) B. \(4x – 4y – 6z + \dfrac{{15}}{2}= 0.\) B. \(4x + 4y + 6z – 7 = 0. \) D. \(x + y – z = 0.\) Câu 19: Trong không gian với hệ trục tọa độ Oxyz cho đường thẳng \(d:\left\{ \begin{array}{l}x = 2 + 2t\\y = - 3t\\z = - 3 + 5t\end{array} \right.(t \in \mathbb{R}).\) Vectơ nào dưới đây là vectơ chỉ phương của d? A.\(\overrightarrow u = (2;0; - 3).\) B.\(\overrightarrow u = (2; - 3;5).\) C.\(\overrightarrow u = (2;3; - 5).\) D.\(\overrightarrow u = (2;0;5).\) Câu 20: Cho đồ thị hàm số y = f(x), diện tích hình phẳng (phần tô đậm trong hình) là: A.\(S = \int\limits_{ - 3}^4 {f(x)dx.} \) B.\(S = \int\limits_0^{ - 3} {f(x)dx + \int\limits_0^4 {f(x)dx} .} \) C.\(S = \int\limits_{ - 3}^1 {f(x)dx + \int\limits_1^4 {f(x)dx} .} \) D.\(S = \int\limits_{ - 3}^0 {f(x)dx - \int\limits_0^4 {f(x)dx} .} \) Câu 21: Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(-2;0;0), B(0;3;0) và C(0;0;2). Phương trình nào dưới đây là phương trình của mặt phẳng (ABC)? A.\(\dfrac{x}{3} + \dfrac{y}{2} + \dfrac{z}{{ - 2}} = 1.\) B.\(\dfrac{x}{2} + \dfrac{y}{{ - 2}} + \dfrac{z}{3} = 1.\) C.\(\dfrac{x}{2} + \dfrac{y}{3} + \dfrac{z}{{ - 2}} = 1.\) D.\(\dfrac{x}{{ - 2}} + \dfrac{y}{3} + \dfrac{z}{2} = 1.\) Câu 22: Phương trình nào sau đây là chính tắc của đường thẳng đi qua hai điểm A(1;2;-3) và B(3;-1;1)? A.\(\dfrac{{x - 1}}{3} = \dfrac{{y - 2}}{{ - 1}} = \dfrac{{z + 3}}{1}.\) B.\(\dfrac{{x - 3}}{1} = \dfrac{{y + 1}}{2} = \dfrac{{z - 1}}{{ - 3}}.\) C.\(\dfrac{{x - 1}}{2} = \dfrac{{y - 2}}{{ - 3}} = \dfrac{{z + 3}}{4}.\) D.\(\dfrac{{x + 1}}{2} = \dfrac{{y + 2}}{{ - 3}} = \dfrac{{z - 3}}{4}.\) Câu 23: Tìm số phức z biết \(z = \dfrac{{3 + 4i}}{{{i^{2019}}}}.\) A. z = 4 – 3i. B. z = 4 + 3i. C. z = 3 – 4i. D. z = 3 + 4i. Câu 24: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x – 2z + 3 = 0. Vectơ nào dưới đây là một vectơ pháp tuyến của (P)? A.\(\overrightarrow n = (1; - 2;0).\) B. \(\overrightarrow n = (1;0; - 2).\) C. \(\overrightarrow n = (3; - 2;1).\) D. \(\overrightarrow n = (1; - 2;3).\) PHẦN II. TỰ LUẬN (4 điểm) Câu 1: (1.0 điểm). Tính các tích phân sau: a) \(I = \int\limits_0^{\sqrt 7 } {x\sqrt[3]{{1 + {x^2}}}} dx;\) \(b)I = \int\limits_0^{\dfrac{\pi }{4}} {(3 - 2x)cos2xdx} .\) Câu 2: (1.0 điểm). a) Giải phương trình (1 + i)z + (4 – 7i) = 8 – 4i. b) Tìm số phức z thỏa mãn: \((3 + i)\overline z + (1 + 2i)z = 3 - 4i.\) Câu 3: (2.0 điểm). Trong không gian với hệ tọa độ Oxyz, cho điểm M(2;1;1) và mặt phẳng (P): 2x – y + 2z + 4 = 0. a) Viết phương trình đường thẳng d đi qua M và vuông góc với mặt phẳng (P). b) Tìm hình chiếu vuông góc của điểm M trên mặt phẳng (P). c) Viết phương trình mặt cầu (S) tâm M và tiếp xúc với mặt phẳng (P). Lời giải chi tiết
PHẦN II. TỰ LUẬN (4 điểm) Câu 1: (1.0 điểm) Tính các tích phân sau:a) \(I = \int\limits_0^{\sqrt 7 } {x\sqrt[3]{{1 + {x^2}}}} dx;\)\(b)I = \int\limits_0^{\dfrac{\pi }{4}} {(3 - 2x)cos2xdx} .\) a) Đặt: \(t = \sqrt[3]{{1 + {x^2}}} \Rightarrow {t^3} = 1 + {x^2}\) \(\Rightarrow 3{t^2}dt = 2xdx \Rightarrow xdx = \dfrac{3}{2}{t^2}dt\) Đổi cận: \(x = 0 \Rightarrow t = 1;x = \sqrt 7 \Rightarrow t = 2 \) \(\Rightarrow I = \int\limits_1^2 {\dfrac{3}{2}} {t^3}dt\)\(\, = \left. {\dfrac{3}{8}} \right|_1^2 = \dfrac{3}{8}(16 - 1) = \dfrac{{45}}{8}.\) b) Đặt \(\left\{ \begin{array}{l}u = 3 - 2x \Rightarrow du = - 2dx\\dv = \cos 2x \Rightarrow v = \dfrac{{\sin 2x}}{2}\end{array} \right.\) \(\begin{array}{l} I = (3 - 2x)\left. {\dfrac{{\sin 2x}}{2}} \right|_0^{\dfrac{\pi }{4}} + \int\limits_0^{\dfrac{\pi }{4}} {\sin 2xdx} \\\;\;\;\;\;\; = \left( {\dfrac{{6 - \pi }}{4}} \right) - \dfrac{1}{2}(0 - 1)\\\,\,\,\,\,\,\,\,\,\, = \dfrac{{8 - \pi }}{4} = 2 - \dfrac{\pi }{4}.\end{array}\) Câu 2: (1.0 điểm) a) Giải phương trình \((1 + i)z + (4 – 7i) = 8 – 4i.\) Ta có: \(\begin{array}{l}(1 + i)z + (4 - 7i) = 8 - 4i\\ \Leftrightarrow (1 + i)z = 4 + 3i\\ \Leftrightarrow z = \dfrac{{4 + 3i}}{{1 + i}} = \dfrac{{(4 + 3i)(1 - i)}}{{(1 + i)(1 - i)}} \\= \dfrac{{4 - 4i + 3i - 3{i^2}}}{2} = \dfrac{7}{2} - \dfrac{1}{2}i\end{array}\) b) Tìm số phức z thỏa mãn: \((3 + i)\overline z + (1 + 2i)z = 3 - 4i.\) Gọi \(z = a + bi\) \((a,b \in \mathbb{R},{i^2} = - 1) \Rightarrow \overline z = a - bi\) \(\begin{array}{l}(3 + i)\overline z + (1 + 2i)z = 3 - 4i\\ \Leftrightarrow (3 + i)(a - bi) + (1 + 2i)(a + bi) \\= 3 - 4i\\ \Leftrightarrow 4a - b + (3a - 2b)i = 3 - 4i\\ \Leftrightarrow \left\{ \begin{array}{l}4a - b = 3\\3a - 2b = - 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 5\end{array} \right.\end{array}\) Vậy \(z = 2 + 5i.\) Câu 3: Trong không gian với hệ tọa độ Oxyz, cho điểm M(2;1;1) và mặt phẳng (P): \(2x – y + 2z + 4 = 0.\) a) Viết phương trình đường thẳng d đi qua M và vuông góc với mặt phẳng (P). Đường thẳng (d) đi qua điểm M(2;1;1), vuông góc với (P) có VTCP: \(\overrightarrow u = (2; - 1;2)\) Có PTTS: \(\left\{ \begin{array}{l}x = 2 + 2t\\y = 1 - t\\z = 1 + 2t\end{array} \right.(t \in \mathbb{R})\) b) Tìm hình chiếu vuông góc của điểm M trên mặt phẳng (P). Tọa độ hình chiếu H của M lên mặt phẳng (P) là nghiệm của hệ: \(\begin{array}{l}\left\{ \begin{array}{l}2x - y + 2z + 4 = 0\\x = 2 + 2t\\y = 1 - t\\z = 1 + 2t\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}t = - 1\\x = 0\\y = 2\\z = - 1\end{array} \right.\end{array}\) Vậy \(H(0;2;-1)\) c) Viết phương trình mặt cầu (S) tâm M và tiếp xúc với mặt phẳng (P). Ta có: \(d(M;(P)) = \dfrac{{\left| {4 - 1 + 2 + 4} \right|}}{{\sqrt {4 + 1 + 4} }} = 3\) Mặt cầu (S) tâm M và tiếp xúc với mặt phẳng (P) có bán kính R = d(M;(P))=2 có phương trình: \({(x - 2)^2} + {(y - 1)^2} + {(z - 1)^2} = 9\) HocTot.XYZ
|