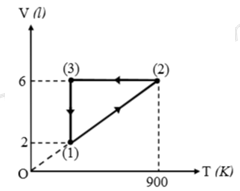
Đề số 8 - Đề kiểm tra học kì 2 - Vật lí 10Đáp án và lời giải chi tiết Đề số 8 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Vật lí 10 Đề bài LÝ THUYẾT: (3đ) Câu 1: Phát biểu và viết biểu thức định lí động năng. Câu 2: Phát biểu và viết biểu thức định luật Boyle - Mariotte về quá trình đẳng nhiệt. Câu 3: Độ nở khối V của một vật rắn phụ thuộc vào yếu tố nào? Nêu hai công thức nở khối. Tại sao khi thời tiết thay đổi nóng, lạnh đột ngột các trụ nhà bê tông vẫn bám chắc vào cốt sắt bên trong, không bị nứt vỡ? BÀI TOÁN: (7đ) Bài 1 (1,5đ): Một khối khí lý tưởng trong xy lanh biến đổi trạng thái theo các quá trình như hình bên. Cho biết áp suất ban đầu của khối khí là p1 = 3 atm.
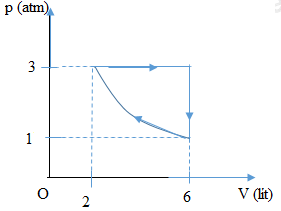
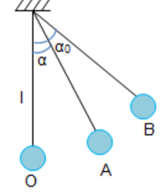
a) Tính nhiệt độ ban đầu T1 và áp suất p3 của khối khí. b) Biểu diễn các quá trình trên trong hệ tọa độ (p,V). Bài 2 (1,5đ): Hai thanh kim loại, một bằng kẽm và một bằng sắt. Khi ở 00C thanh kẽm có chiều dài l01 = 50 cm, thanh sắt có chiều dài l02. Khi ở 900C cả 2 thanh có chiều dài bằng nhau. Tính l02. Biết hệ số nở dài của kẽm là 3,1.10-5 K-1, hệ số nở dài của sắt là 1,14.10-5 K-1. Bài 3 (1,0đ): Người ta thực hiện công 100 J để nén khí trong một xy lanh. Khí truyền ra môi trường xung quanh nhiệt lượng 15 J. Nội năng của khí trong xy lanh tăng hay giảm một lượng bao nhiêu? Bài 4 (2,0đ): Một xe khối lượng 2 tấn, bắt đầu chuyển động nhanh dần đều từ A trên đường nằm ngang AB dài 20 m. Lực kéo của động cơ không đổi là F = 5200 N. Hệ số ma sát trên mặt đường ngang là 0,1. Lấy g = 10 m/s2. (Giải bài toán bằng cách dùng các định luật bảo toàn) a) Tính vận tốc của xe tại B. b) Đến B, xe tắt máy và đi lên dốc nghiêng góc 180 so với phương ngang. Bỏ qua ma sát. Tìm quãng đường tối đa xe đi được trên dốc. c) Đến B, xe tắt máy và đi lên dốc nghiêng góc 180 so với phương ngang. Hệ số ma sát trên mặt dốc là 0,2. Tìm quãng đường tối đa xe đi được trên dốc. Bài 5 (1,0đ): Một con lắc đơn có chiều dài 0,8 m. Kéo lệch dây treo con lắc hợp với phương thẳng đứng góc 600 rồi thả nhẹ. Bỏ qua lực cản không khí. Lấy g = 10 m/s2. Tính tốc độ cực đại của con lắc đạt được trong quá trình dao động. Lời giải chi tiết LÍ THUYẾT Câu 1: Phương pháp: Độ biến thiên động năng của một vật bằng công của ngoại lực tác dụng vào vật. \({A_{12}} = {{\rm{W}}_{d2}} - {{\rm{W}}_{d1}} = \Delta {{\rm{W}}_d} \) \(= \dfrac{1}{2}.m.v_2^2 - \dfrac{1}{2}.m.v_1^2\) Cách giải: Độ biến thiên động năng của một vật bằng công của ngoại lực tác dụng vào vật. \({A_{12}} = {{\rm{W}}_{d2}} - {{\rm{W}}_{d1}}\) \(= \Delta {{\rm{W}}_d} = \dfrac{1}{2}.m.v_2^2 - \dfrac{1}{2}.m.v_1^2\) Câu 2: Phương pháp: Định luật Bôi lơ - Ma ri ôt: Trong quá trình đẳng nhiệt của một lượng khí nhất định, áp suất tỉ lệ nghịch với thể tích. Biểu thức: \(p.V = const\) hay \({p_1}.{V_1} = {p_2}.{V_2}\) Cách giải: Định luật Bôi lơ - Ma ri ôt: Trong quá trình đẳng nhiệt của một lượng khí nhất định, áp suất tỉ lệ nghịch với thể tích. Biểu thức: \(p.V = const\) hay \({p_1}.{V_1} = {p_2}.{V_2}\) Câu 3: Độ nở khối ∆V của một vật rắn phụ thuộc bản chất của chất làm vật, thể tích ban đầu và độ thay đổi nhiệt độ ∆t. Công thức nở khối: \(\Delta V = \beta .{V_0}.\Delta t\) hay \(V = {V_0}.\left( {1 + \beta .\left( {t - {t_0}} \right)} \right)\) Vì bê tông và cốt sắt có hệ số nở vì nhiệt gần bằng nhau nên khi nhiệt độ thay đổi, độ nở của chúng như nhau nên vẫn bám chắc vào nhau. BÀI TOÁN Bài 1: Phương pháp: Quá trình (1) → (2): đẳng áp; (2) → (3): đẳng tích; (3) → (1): đẳng nhiệt. Áp dụng công thức cho các đẳng quá trình Đẳng nhiệt: \({p_1}.{V_1} = {p_2}.{V_2}\) Đẳng áp: \(\dfrac{{{V_1}}}{{{T_1}}} = \dfrac{{{V_2}}}{{{T_2}}}\) Đẳng tích: \(\dfrac{{{p_1}}}{{{T_1}}} = \dfrac{{{p_2}}}{{{T_2}}}\) Từ các số liệu tính toán được vẽ đồ thị trong hệ tọa độ pOV. Cách giải: Quá trình (1) → (2): đẳng áp; (2) → (3): đẳng tích; (3) → (1): đẳng nhiệt. Áp dụng cho quá trình đẳng áp: \(\frac{{{V_1}}}{{{T_1}}} = \frac{{{V_2}}}{{{T_2}}} \Rightarrow {T_1} = {T_2}.\frac{{{V_1}}}{{{V_2}}} = 300K\) Áp dụng định luật Bôi lơ – Ma ri ôt: \({p_1}.{V_1} = {p_3}.{V_3} \Rightarrow {p_3} = {p_1}.\frac{{{V_1}}}{{{V_3}}} = 1atm\) Vậy ta có các trạng thái được biến đổi theo sơ đồ sau: \(\left\{ \begin{array}{l}{p_1} = 3atm\\{V_1} = 2l\\{T_1} = 300K\end{array} \right. \to \left\{ \begin{array}{l}{p_2} = {p_1} = 3atm\\{V_2} = 6l\\{T_2} = 900K\end{array} \right. \) \(\to\left\{ \begin{array}{l}{p_3} = 1atm\\{V_3} = 6l\\{T_3} = 300K\end{array} \right. \to \left\{ \begin{array}{l}{p_1} = 3atm\\{V_1} = 2l\\{T_1} = 300K\end{array} \right.\) Từ đó ta vẽ được đồ thị thể hiện quá trình biến đổi trong hệ pOV như sau: Bài 2: Phương pháp: Áp dụng công thức về độ nở dài: \(l = {l_0}.(1 + \alpha \Delta t)\) Cách giải: Áp dụng công thức về độ nở dài, ta có: \({}{l_{Zn}} = {l_{{0_{Zn}}}}.(1 + {\alpha _{Zn}}.\Delta t)\) \(= 50.(1 + 3,{1.10^{ - 5}}.90)\) \(= 50,{1395_{}}cm = 0,{501395_{}}m\\{l_{Zn}} = {l_{Fe}} = {l_{{0_{Fe}}}}.(1 + 1,{14.10^{ - 5}}.90)\) \(= 50,{139_{}}cm\\ \Rightarrow {l_{{0_{Fe}}}} = 50,{088_{}}cm = 0,{50088_{}}m\) Bài 3: Phương pháp: Áp dụng công thức định Lý I – NĐLH: \(\Delta U = A + Q\) Với A> 0 khi hệ nhận công; A < 0 khi hệ thực hiện công Và Q > 0 khi hệ nhận nhiệt; Q < 0 khi hệ tỏa nhiệt. Cách giải: Vì hệ nhận công và toả nhiệt nên: \(\left\{ \begin{array}{l}A = 100{\rm{ }}J\\Q = - 15{\rm{ }}J\end{array} \right.\) Ta có độ biến thiên nội năng của hệ là: \(\Delta U = A + Q = 100--15 = 85{\rm{ }}J\) Vậy nội năng của khí tăng 85 J. Bài 4: Phương pháp: Áp dụng định lý động năng: \(\frac{1}{2}.m.{v^2} - \frac{1}{2}.m.v_0^2 = {A_{ms}} + {A_{Fk}}\) Cách giải: Tóm tắt: \(\begin{array}{l}m = 2T = 2000{\rm{ }}kg\\F = 5200N;S = 20m\\\mu = 0,1;g = 10{\rm{ }}m/{s^2}\end{array}\) a) Tính vận tốc ở cuối đường. b) Đến B, xe tắt máy và đi lên dốc nghiêng góc 180 so với phương ngang. Bỏ qua ma sát. Tìm quãng đường tối đa xe đi được trên dốc c) Đến B, xe tắt máy và đi lên dốc nghiêng góc 180 so với phương ngang. Hệ số ma sát trên mặt dốc là 0,2. Tìm quãng đường tối đa xe đi được trên dốc. Bài làm: a) Áp dụng định lý động năng: \(\dfrac{1}{2}.m.{v^2} - \dfrac{1}{2}.m.v_0^2 \) \(= {A_{ms}} + {A_{Fk}}\,\,\,\left( {{v_0} = 0} \right)\) Ta có: \({}\frac{1}{2}.m.{v^2} - \frac{1}{2}.m.v_0^2 = {A_{ms}} + {A_{Fk}}\\ \) \(\Rightarrow \frac{1}{2}.m.{v^2} = \mu .m.g.s + F.s\\\) \(\Rightarrow \frac{1}{2}.2000.{v^2} \) \(= - 0,1.2000.10.20 + 5200.20 \) \(\Rightarrow v = 8\left( {m/s} \right)\) Vậy vB = 8 m/s. b) Áp dụng định lý động năng ta có: \(0 - \frac{1}{2}.m.{v^2} = - m.g.S.\sin \alpha \) \(\Rightarrow {S_{\max }} = 10,{36_{}}m\) c) Áp dụng định lý động năng ta có: \({} - \frac{1}{2}.m.{v^2} \) \(= - m.g.S.\sin \alpha - \mu .m.g.S.sin\alpha \\ \Rightarrow - \frac{1}{2}{.2000.8^2} \) \(= - 2000.10.S.\sin {18^0} \) \(- 0,2.2000.10.S.\sin {18^0}\\ \Rightarrow {S_{\max }} = 6,{41_{}}m\) Bài 5: Phương pháp: Áp dụng định luật bảo toàn cơ năng Cách giải: Chọn gốc thế năng tại O. Áp dụng định luật bảo toàn cơ năng tại O và B ta có: \({}\frac{1}{2}mv_{\max }^2 = mgl.\left( {1 - \cos {\alpha _0}} \right)\\ \Rightarrow {v_{\max }} = \sqrt {2gl.\left( {1 - \cos {\alpha _0}} \right)} \) \(= \sqrt {2.10.0,8.\left( {1 - \cos 60} \right)} \) \(= 2\sqrt 2 m/s\) Nguồn: Sưu tầm HocTot.XYZ
|