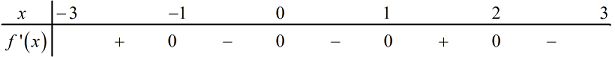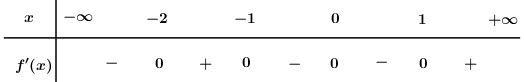Phương pháp giải:

Điểm $x = {x_0}$ là điểm cực đại của hàm số $y = f\left( x \right)$ khi là nghiệm của hệ $\left\{ \begin{array}{l}f'\left( {{x_0}} \right) = 0\\f''\left( {{x_0}} \right) < 0\end{array} \right.$.

Lời giải chi tiết:

Ta có: $y' = 40{x^3} + 10x = 10x\left( {4{x^2} + 1} \right)$, $y'' = 120{x^2} + 10 > 0\,\,\forall x \in \mathbb{R}$.

Do đó hàm số không có điểm cực đại.

Chọn D.

Phương pháp giải:

Lập bảng xét dấu của $f'\left( x \right)$ và xác định các điểm cực trị là các điểm mà qua đó $f'\left( x \right)$ đổi dấu.

Lời giải chi tiết:

Ta có: $f'\left( x \right) = {x^2}\left( {x - 1} \right),\,\forall x \in \mathbb{R},\,\,\,\,f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.$

Bảng xét dấu $f'\left( x \right)$:

Vậy, hàm số đạt cực tiểu tại $x = 1$.

Chọn C.

Phương pháp giải:

Điểm $x = {x_0}$là điểm cực tiểu của hàm số $y = f\left( x \right)$ khi và chỉ khi$\left\{ \begin{array}{l}f'\left( {{x_0}} \right) = 0\\f''\left( {{x_0}} \right) > 0\end{array} \right.$.

Lời giải chi tiết:

TXĐ: $D = \mathbb{R}$.

Ta có: $y' = 3{x^2} - 3,\,\,y'' = 6x$.

Xét hệ phương trình $\left\{ \begin{array}{l}y' = 0\\y'' > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3{x^2} - 3 = 0\\6x > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  \pm 1\\x > 0\end{array} \right. \Leftrightarrow x = 1$.

Vậy điểm cực tiểu của hàm số đã cho là $x = 1$.

Chọn C.

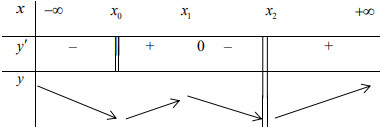
Phương pháp giải:

Số cực trị của hàm số $y = f\left( x \right)$ là số nghiệm bội lẻ của phương trình $f'\left( x \right) = 0.$

Lời giải chi tiết:

Xét hàm số $y = 3{x^4} - 4{x^2} + 1$ ta có:

TXĐ: $D = \mathbb{R}$

Ta có:$y' = 12{x^3} - 8x$

$\begin{array}{l} \Rightarrow y' = 0 \Leftrightarrow 12{x^3} - 8x = 0 \Leftrightarrow 4x\left( {3{x^2} - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}4x = 0\\3{x^2} - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \dfrac{{\sqrt 6 }}{3}\\x =  - \dfrac{{\sqrt 6 }}{3}\end{array} \right.\end{array}$

$\Rightarrow$  Phương trình $y' = 0$ có 3 nghiệm đơn phân biệt $\Rightarrow$ Hàm số đã cho có 3 điểm cực trị.

Chọn D.

Phương pháp giải:

- Điểm $x = {x_0}$ được gọi là điểm cực tiểu của hàm số nếu hàm số liên tục tại ${x_0}$ và qua đó $y'$ đổi dấu từ âm sang dương.

- Điểm $x = {x_0}$ được gọi là điểm cực đại của hàm số nếu hàm số liên tục tại ${x_0}$ và qua đó $y'$ đổi dấu từ dương sang âm.

Lời giải chi tiết:

Dựa vào BBT ta thấy hàm số đạt cực tiểu tại $x = {x_0}$ và đạt cực đại tại $x = {x_1}$ (hàm số không đạt cực tiểu tại $x = {x_2}$ do không xác định tại ${x_2}$).

Chọn A.

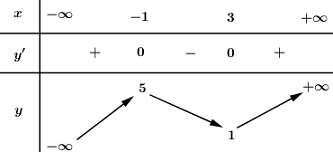
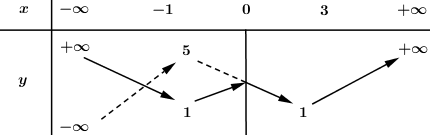
Phương pháp giải:

Hàm số $y = a{x^4} + b{x^2} + c\,\,\left( {a \ne b} \right)$ chỉ có cực tiểu mà không có cực đại khi và chỉ khi $a > 0,\,\,b \ge 0$.

Lời giải chi tiết:

TH1: $m + 1 = 0 \Leftrightarrow m =  - 1$, khi đó hàm số trở thành $y = {x^2} + \dfrac{3}{2}$ là một parabol có bề lõm hướng lên nên có 1 cực tiểu mà không có cực đại, do đó $m =  - 1$ thỏa mãn.

TH2: $m + 1 \ne 0 \Leftrightarrow m \ne  - 1$.

Để hàm số $y = \left( {m + 1} \right){x^4} - m{x^2} + \dfrac{3}{2}$ chỉ có cực tiểu mà không có cực đại khi và chỉ khi $a > 0,\,\,b \ge 0$.

$\Rightarrow \left\{ \begin{array}{l}m + 1 > 0\\ - m \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m >  - 1\\m \le 0\end{array} \right. \Leftrightarrow  - 1 < m \le 0$.

Vậy $- 1 \le m \le 0$.

Chọn B.

Phương pháp giải:

- Từ BBT của đồ thị hàm số $y = f\left( x \right)$ vẽ BBT của đồ thị hàm số $y = f\left( {\left| x \right|} \right)$:

   + Giữ nguyên phần đồ thị bên phải trục $Oy$.

   + Xóa đi phần đồ thị bên trái trục $Oy$.

   + Lấy đối xứng phần đồ thị bên phải trục $Oy$ qua trục $Oy$.

- Dựa vào BBT xác định các điểm cực trị: điểm mà qua đó hàm số chuyển hướng.

Lời giải chi tiết:

Dựa vào BBT đồ thị hàm số $y = f\left( x \right)$ suy ra BBT đồ thị hàm số $y = f\left( {\left| x \right|} \right)$ như sau:

Dựa vào BBT ta thấy hàm số $y = f\left( {\left| x \right|} \right)$ có 3 điểm cực trị.

Chọn B.

Phương pháp giải:

Số điểm cực trị của hàm số $y = f\left( x \right)$ là số nghiệm bội lẻ của phương trình $f'\left( x \right) = 0$.

Lời giải chi tiết:

Ta có: $f'\left( x \right) = 0 \Leftrightarrow x{\left( {x - 1} \right)^2}.{\left( {x - 2} \right)^3} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\\x = 2\end{array} \right.$, trong đó $x = 0$ là nghiệm bội 1, $x = 1$ là nghiệm bội 2, $x = 2$ là nghiệm bội 3.

Vậy hàm số đã cho có 2 điểm cực trị $x = 0,\,\,x = 1$.

Chọn C.

Phương pháp giải:

Ta có: $x = {x_0}$ là điểm cực trị của hàm số $y = f\left( x \right) \Leftrightarrow$ tại điểm $x = {x_0}$ thì hàm số có $y'$  đổi dấu từ dương sang âm hoặc ngược lại.

Lời giải chi tiết:

Dựa vào bảng xét dấu của hàm số $y = f\left( x \right)$ ta thấy $f'\left( x \right)$ đổi dấu qua $x =  - 1,\,\,x = 0,\,\,x = 2$ và $x = 4$

$\Rightarrow 4$ điểm này là $4$ điểm cực trị của hàm số $y = f\left( x \right).$

Vậy hàm số $y = f\left( x \right)$ có $4$ điểm cực trị.

Chọn A.

Phương pháp giải:

Số điểm cực trị của đồ thị hàm số $y = f\left( x \right)$  là số nghiệm bội lẻ của phương trình $f'\left( x \right) = 0.$

Điểm$x = {x_0}$ là điểm cực đại của hàm số $y = f\left( x \right) \Leftrightarrow$ tại điểm $x = {x_0}$ thì hàm số có $y'$  đổi dấu từ dương sang âm.

Lời giải chi tiết:

Ta có: $f'\left( x \right) = 0$

$\begin{array}{l} \Leftrightarrow \left( {{x^3} - 1} \right)\left( {{x^2} - 3x + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}{x^3} - 1 = 0\\{x^2} - 3x + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^3} = 1\\\left( {x - 1} \right)\left( {x - 2} \right) = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\\x - 1 = 0\\x - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 1\\x = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.\end{array}$

Ta thấy $x = 1$ là nghiệm bội 4 của phương trình $f'\left( x \right) = 0$$\Rightarrow x = 1$ không là điểm cực trị của hàm số.

Ta có bảng xét dấu:

Ta thấy qua điểm $x = 2$ thì $f'\left( x \right)$ đổi dấu từ âm sang dương nên $x = 2$ là điểm cực tiểu của hàm số.

$\Rightarrow$ Hàm số không có điểm cực đại.

Chọn A.

Phương pháp giải:

Ta có: $x = {x_0}$ là điểm cực trị của hàm số $y = f\left( x \right) \Leftrightarrow$ tại điểm $x = {x_0}$ thì hàm số có $y'$  đổi dấu từ dương sang âm hoặc ngược lại.

Lời giải chi tiết:

Dựa vào bảng xét dấu của hàm số $y = f\left( x \right)$ trong khoảng $\left( { - 3;\,\,3} \right)$ ta thấy $f'\left( x \right)$ đổi dấu qua các điểm $x =  - 1,\,\,x = 1$ và $x = 2.$

$\Rightarrow$ Hàm số $y = f\left( x \right)$ có 3 điểm cực trị.

Chọn B. 

Phương pháp giải:

- Xét dấu đạo hàm.

- Điểm cực đại của hàm số là điểm mà qua đó $f'\left( x \right)$ đổi dấu từ dương sang âm.

Lời giải chi tiết:

Ta có $f'\left( x \right) = 0 \Leftrightarrow {x^2}\left( {{x^2} - 1} \right)\left( {x + 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  \pm 1\\x =  - 2\end{array} \right.$.

Bảng xét dấu $f'\left( x \right)$:

Dựa vào bảng xét dấu ta thấy hàm số đạt cực đại tại $x =  - 1$.

Vậy hàm số đã cho có 1 điểm cực đại.

Chọn A.

Phương pháp giải:

Ta có: $x = {x_0}$ là điểm cực trị của hàm số $y = f\left( x \right) \Leftrightarrow$ tại điểm $x = {x_0}$ thì hàm số có $y'$  đổi dấu từ dương sang âm hoặc ngược lại.

Hay số điểm cực trị của hàm số là số lần đổi dấu của $f'\left( x \right).$

Lời giải chi tiết:

Dựa vào bảng xét dấu ta thấy $f'\left( x \right)$ đổi dấu qua $x =  - 1,\,\,\,x = 0$ và $x = 2$ nên hàm số có 3 điểm cực trị.

Chọn D.

Phương pháp giải:

Xác định số điểm mà đạo hàm đổi dấu từ dương sang âm.

Lời giải chi tiết:

$\begin{array}{l}f'\left( x \right) = {x^2}\left( {{x^2} - 4} \right)\left( {{x^2} - 3x + 2} \right)\left( {x - 3} \right)\\\,f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  \pm 2\\x = 1\\x = 2\,\\x = 3\,\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  \pm 2\\x = 1\,\\x = 3\,\end{array} \right.\end{array}$

Trong đó $x =  - 2,\,\,x = 1,\,\,x = 3$ là các nghiệm đơn, $x = 0,\,\,x = 2$ là nghiệm bội 2.

Ta có bảng xét dấu $f'\left( x \right)$ như sau:

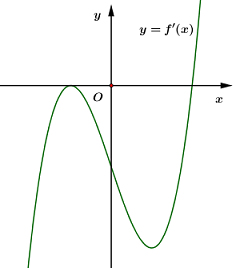
Vậy hàm số đạt cực đại tại 1 điểm là $x = 1$.

Chọn A.

Phương pháp giải:

Số điểm cực trị của đồ thị hàm số $y = f\left( x \right)$  là số nghiệm bội lẻ của phương trình $f'\left( x \right) = 0.$

Hoặc số điểm cực trị của đồ thị hàm số $y = f\left( x \right)$  là số lần đổi dấu của $f'\left( x \right).$  

Lời giải chi tiết:

Dựa vào đồ thị hàm số $y = f'\left( x \right)$ ta thấy $f'\left( x \right)$ có 1 lần đổi dấu từ âm sang dương

$\Rightarrow$ Hàm số $y = f\left( x \right)$ có 1 điểm cực trị.

Chọn D.

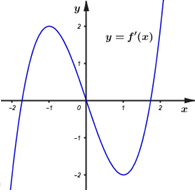
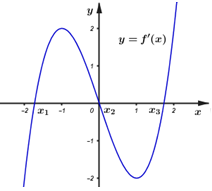
Phương pháp giải:

Số điểm cực tiểu của hàm số $y = f\left( x \right)$ là số lần đổi dấu từ âm sang dương của $f'\left( x \right).$

Lời giải chi tiết:

Dựa vào bảng xét dấu của $f'\left( x \right)$ ta thấy $f'\left( x \right)$ đổi dấu từ âm sang dương qua các điểm $x =  - 1$ và $x = 1$

$\Rightarrow$ Hai điểm này là hai điểm cực tiểu của hàm số $y = f\left( x \right).$

Chọn B.

Phương pháp giải:

Điểm $x = {x_0}$ là điểm cực tiểu của hàm số $y = f\left( x \right) \Leftrightarrow$ tại điểm $x = {x_0}$ thì hàm số có $y'$  đổi dấu từ âm sang dương.

Điểm $x = {x_0}$ là điểm cực đại của hàm số $y = f\left( x \right) \Leftrightarrow$ tại điểm $x = {x_0}$ thì hàm số có $y'$  đổi dấu từ dương sang âm.

Lời giải chi tiết:

Dựa vào đồ thị hàm số ta thấy:

Qua điểm ${x_1},\,\,{x_3}$ thì $f'\left( x \right)$ đổi dấu từ âm sang dương $\Rightarrow {x_1},\,\,{x_3}$ là hai điểm cực tiểu của hàm số.

$\Rightarrow m = 2$

Qua điểm ${x_2}$ thì $f'\left( x \right)$ đổi dấu từ dương sang âm $\Rightarrow {x_2}$ là điểm cực tiểu của hàm số.

$\begin{array}{l} \Rightarrow n = 1\\ \Rightarrow 2m - n = 2.2 - 1 = 3.\end{array}$

Chọn A.

Phương pháp giải:

Hàm số $y = f\left( x \right)$ có hai điểm cực trị khi và chỉ khi phương trình $f'\left( x \right) = 0$ có hai nghiệm phân biệt.

Lời giải chi tiết:

TXĐ: $D = \mathbb{R}$. Ta có $y' = 3{x^2} - 6x + m$.

Để hàm số đã cho có 2 điểm cực trị thì phương trình $y' = 0$ phải có 2 nghiệm phân biệt.

$\Leftrightarrow \Delta ' > 0$ $\Leftrightarrow {3^2} - 3m > 0 \Leftrightarrow 9 - 3m > 0$ $\Leftrightarrow m < 3$.

Chọn B.

Phương pháp giải:

Hàm số $y = f\left( x \right)$ đạt cực đại tại ${x_0}$ khi liên tục tại ${x_0}$ và $\left\{ \begin{array}{l}f'\left( {{x_0}} \right) = 0\\f''\left( {{x_0}} \right) < 0\end{array} \right.$.

Lời giải chi tiết:

Ta có: $y' = {x^2} + x + m - 4$ ; $y'' = 2x + 1$.

Hàm số $y = \dfrac{{{x^3}}}{3} + \dfrac{{{x^2}}}{2} + \left( {m - 4} \right)x - 7$ đạt cực đại tại $x = 1$ khi và chỉ khi:

$\left\{ \begin{array}{l}y'\left( 1 \right) = 0\\y''\left( 1 \right) < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{1^2} + 1 + m - 4 = 0\\2.1 + 1 < 0\,\,\left( {Vo\,\,ly} \right)\end{array} \right.$.

Vậy không có $m$ để hàm số đạt cực đại tại $x = 1$.

Chọn D.

Phương pháp giải:

- Giải hệ phương trình .. để tìm điểm cực tiểu của hàm số.

- Tính giá trị cực tiểu của hàm số.

Lời giải chi tiết:

TXĐ: $D = \mathbb{R}$.

Ta có: $f'\left( x \right) =  - 4{x^3} + 8x$, $f''\left( x \right) =  - 12{x^2} + 8$.

Xét hệ $\left\{ \begin{array}{l}f'\left( x \right) = 0\\f''\left( x \right) > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 4{x^3} + 8x = 0\\ - 12{x^2} + 8 = 0\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x = 0\\x =  \pm \sqrt 2 \end{array} \right.\\ - 12{x^2} + 8 = 0\end{array} \right. \Leftrightarrow x = 0$.

Vậy điểm cực tiểu của hàm số là ${x_{CT}} = 0$, giá trị cực tiểu của hàm số là ${y_{CT}} = y\left( 0 \right) = 3$.

Chọn C.

Phương pháp giải:

- Xác định điểm cực đại của hàm số bằng cách giải hệ phương trình $\left\{ \begin{array}{l}y' = 0\\y'' < 0\end{array} \right.$.

- Tính giá trị cực đại ${y_{CD}}$.

Lời giải chi tiết:

Ta có: $f'\left( x \right) = 2.2x\left( {{x^2} - 3} \right) = 4{x^3} - 12x$ $\Rightarrow f''\left( x \right) = 12{x^2} - 12,\,\,f'''\left( x \right) = 24x$

Xét hệ phương trình $\left\{ \begin{array}{l}f''\left( x \right) = 0\\f'''\left( x \right) < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}12{x^2} - 12 = 0\\24x < 0\end{array} \right. \Leftrightarrow x =  - 1$

Do đó điểm cực đại của hàm số là $x =  - 1$.

Vậy giá trị cực đại của hàm số là $y{'_{CD}} = y'\left( { - 1} \right) = 8$.

Chọn B.

Phương pháp giải:

Hàm số bậc ba có 2 cực trị khi và chỉ khi $y' = 0$ có hai nghiệm phân biệt.

Lời giải chi tiết:

TXĐ: $D = \mathbb{R}$.

$y = {x^3} - m\,{x^2} + 3x - 3 \Rightarrow y' = 3{x^2} - 2mx + 3$

Để hàm số có 2 điểm cực trị thì phương trình $y' = 0$ phải có 2 nghiệm phân biệt $\Leftrightarrow \Delta ' = {m^2} - 9 > 0 \Leftrightarrow \left[ \begin{array}{l}m > 3\\m <  - 3\end{array} \right.$.

Chọn B.

Phương pháp giải:

Hai điểm cực trị x₁, x₂ của đồ thị hàm số bậc ba nằm về 2 phía trục Oy$\Leftrightarrow {x_1}.{x_2} < 0$.

Lời giải chi tiết:

$y = \dfrac{{ - 1}}{3}{x^3} - 2m{x^2} + mx + 1 \Rightarrow y' =  - {x^2} - 4mx + m$

Đồ thị hàm số có 2 điểm cực trị x₁, x₂ nằm về 2 phía trục Oy $\Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\{x_1}.{x_2} < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4{m^2} + m > 0\\ - m < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 0\\m <  - \dfrac{1}{4}\end{array} \right.\\m > 0\end{array} \right. \Leftrightarrow m > 0$

Chọn B.

Phương pháp giải:

Số điểm cực trị của hàm số $y = f\left( x \right)$ là số nghiệm bội lẻ của phương trình $f'\left( x \right) = 0$.

Lời giải chi tiết:

Ta có:

$\begin{array}{l}f'\left( x \right) = {x^{2017}}.{\left( {x - 1} \right)^{2018}}.{\left( {x + 1} \right)^{2019}},\,\,\forall x \in \mathbb{R}\\f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\\x =  - 1\end{array} \right.\end{array}$

Trong đó:

+ $x = 0$ là nghiệm bội $2017$ (là cực trị).

+ $x = 1$ là nghiệm bội $2018$ (không là cực trị).

+ $x =  - 1$ là nghiệm bội $2019$ (là cực trị).

Vậy hàm số đã cho có 2 điểm cực trị.

Chọn C.

Phương pháp giải:

Khảo sát hàm số đã cho, tìm các điểm cực trị của hàm số.

Giả sử ba điểm cực trị của đồ thị hàm số là $A\left( {0;\,\,{y_0}} \right),\,\,B\left( {{x_1};\,\,{y_1}} \right),\,\,C\left( {{x_2};\,\,{y_1}} \right).$

Khi đó ta có: $\Delta ABC$ cân tại $A$ và tính diện tích $\Delta ABC$ bằng công thức: ${S_{ABC}} = \frac{1}{2}\left| {{y_0}} \right|.BC.$

Lời giải chi tiết:

Xét hàm số $y = {x^4} - 2{x^2} + 1$ ta có:

$\begin{array}{l}y' = 4{x^3} - 4x \Rightarrow y' = 0 \Leftrightarrow 4{x^3} - 4x = 0\\ \Leftrightarrow 4x\left( {{x^2} - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0 \Rightarrow A\left( {0;\,\,1} \right)\\x =  - 1 \Rightarrow B\left( { - 1;\,\,0} \right)\\x = 1 \Rightarrow C\left( {1;\,\,0} \right)\end{array} \right..\end{array}$

$\Rightarrow$ Đồ thị hàm số có ba điểm cực trị là: $A\left( {0;\,1} \right),\,\,B\left( { - 1;\,\,0} \right),\,\,C\left( {1;\,\,\,0} \right)$ tạo thành $\Delta ABC$ cân tại $A.$

Ta có: $\overrightarrow {BC}  = \left( {2;\,\,0} \right) \Rightarrow BC = 2.$

$\Rightarrow {S_{ABC}} = \frac{1}{2}d\left( {A;\,BC} \right) = BC$ $= \frac{1}{2}\left| {{y_A}} \right|.BC = \frac{1}{2}.1.2 = 1.$

Chọn D. 

Phương pháp giải:

Số điểm cực trị của hàm số $y = \left| {f\left( x \right)} \right|$ là $S = a + b$ với $a$ là số cực trị của hàm số $y = f\left( x \right)$ và $b$ là số giao điểm của đồ thị hàm số $y = f\left( x \right)$ với trục $Ox.$

Lời giải chi tiết:

Xét hàm số $y = {x^2} - 3x + 2$ ta có: $y' = 2x - 3 \Rightarrow y' = 0$ $\Leftrightarrow 2x - 3 = 0$ $\Leftrightarrow x = \dfrac{3}{2}$

$\Rightarrow$ Hàm số $y = {x^2} - 3x + 2$ có 1 cực trị.

Xét phương trình hoành độ giao điểm của đồ thị hàm số $y = {x^2} - 3x + 2$ với trục hoành ta có:

${x^2} - 3x + 2 = 0$ $\Leftrightarrow \left( {x - 1} \right)\left( {x - 2} \right) = 0$$\Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.$

$\Rightarrow$ Đồ thị hàm số $y = {x^2} - 3x + 2$ cắt trục hoành tại 2 điểm phân biệt.

$\Rightarrow$ Số điểm cực trị của hàm số $y = \left| {{x^2} - 3x + 2} \right|$ là: $S = 1 + 2 = 3$ cực trị.

Chọn B.

Phương pháp giải:

Hàm số nhận điểm $x = {x_0}$ là điểm cực trị khi $f'\left( x \right)$ đổi dấu khi qua ${x_0}$.

Lời giải chi tiết:

Dựa vào đồ thị ta thấy hàm số $y = f'\left( x \right)$ đổi dấu khi đi qua điểm $x = 2$.

Vậy hàm số $y = f\left( x \right)$ có 1 điểm cực trị.

Chọn D.

Phương pháp giải:

Số điểm cực trị của đồ thị hàm số $y = f\left( x \right)$  là số nghiệm bội lẻ của phương trình $f'\left( x \right) = 0.$

Lời giải chi tiết:

Ta có: $f'\left( x \right) = 0$

$\begin{array}{l} \Leftrightarrow \left( {x - 1} \right)\left( {{x^2} - 3x + 2} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 1} \right)\left( {x - 2} \right) = 0\\ \Leftrightarrow {\left( {x - 1} \right)^2}\left( {x - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\,\,\,\,\left( {boi\,\,2} \right)\\x = 2\,\,\,\left( {boi\,\,1} \right)\end{array} \right.\end{array}$

$\Rightarrow$ Hàm số $y = f\left( x \right)$ có một điểm cực trị là: $x = 2.$ 

Chọn A.

Phương pháp giải:

Ta có: $x = {x_0}$ là điểm cực trị của hàm số $y = f\left( x \right) \Rightarrow f'\left( {{x_0}} \right) = 0.$

Điểm $x = {x_0}$ là điểm cực đại của hàm số $y = f\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}f'\left( {{x_0}} \right) = 0\\f''\left( {{x_0}} \right) < 0\end{array} \right..$

Điểm $x = {x_0}$ là điểm cực tiểu của hàm số $y = f\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}f'\left( {{x_0}} \right) = 0\\f''\left( {{x_0}} \right) > 0\end{array} \right..$

Lời giải chi tiết:

+) Đáp án A: sai vì hàm số có điểm cực trị tại $x = {x_0}$ nhưng $f''\left( {{x_0}} \right) = 0$

Ví dụ hàm số: $y = {x^4} \Rightarrow y' = 4{x^3} \Rightarrow y'' = 4{x^2}$

Hàm số có điểm cực tiểu $x = 0$ và $y''\left( 0 \right) = 0.$

+) Đáp án B đúng.

Chọn  B.

Phương pháp giải:

Điểm $x = {x_0}$ là điểm cực tiểu của hàm số $y = f\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}f'\left( {{x_0}} \right) = 0\\f''\left( {{x_0}} \right) > 0\end{array} \right..$

Lời giải chi tiết:

Ta có: $y = m{x^3} + {x^2} + \left( {{m^2} - 6} \right)x + 1$

$\begin{array}{l} \Rightarrow y' = 3m{x^2} + 2x + {m^2} - 6\\ \Rightarrow y'' = 6mx + 2\end{array}$

Hàm số $y = m{x^3} + {x^2} + \left( {{m^2} - 6} \right)x + 1$ đạt cực tiểu tại $x = 1$  

$\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}y'\left( 1 \right) = 0\\y''\left( 1 \right) > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3m + 2 + {m^2} - 6 = 0\\6m + 2 > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{m^2} + 3m - 4 = 0\\m >  - \frac{1}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 1\\m =  - 4\end{array} \right.\\m >  - \frac{1}{3}\end{array} \right. \Leftrightarrow m = 1.\end{array}$

Chọn D.