Phương pháp giải:

- Giải phương trình bậc hai trên tập số phức với hệ số thực xác định các nghiệm ${z_1},\,\,{z_2}$.

- Thay ${z_1},\,\,{z_2}$ vào biểu thức ${\left| {{z_1} + i} \right|^2} + {\left| {{z_2} + i} \right|^2}$, sử dụng công thức $\left| {a + bi} \right| = \sqrt {{a^2} + {b^2}}$.

Lời giải chi tiết:

Ta có: ${z^2} - 4z + 13 = 0 \Leftrightarrow \left[ \begin{array}{l}{z_1} = 2 + 3i\\{z_2} = 2 - 3i\end{array} \right.$.

Khi đó:

$\begin{array}{l}\,\,\,\,{\left| {{z_1} + i} \right|^2} + {\left| {{z_2} + i} \right|^2}\\ = {\left| {2 + 3i + i} \right|^2} + {\left| {2 - 3i + i} \right|^2}\\ = {\left| {2 + 4i} \right|^2} + {\left| {2 - 2i} \right|^2}\\ = \left( {{2^2} + {4^2}} \right) + \left( {{2^2} + {2^2}} \right) = 28\end{array}$

Chọn A.

Phương pháp giải:

- Giải phương trình tìm nghiệm phức ${z_1},\,\,{z_2}$.

- Tính $\left| {z_1^2} \right| + \left| {z_2^2} \right|$.

Lời giải chi tiết:

Ta có: ${z^2} + 2z + 5 = 0 \Leftrightarrow \left[ \begin{array}{l}{z_1} =  - 1 + 2i\\{z_2} =  - 1 - 2i\end{array} \right.$.

Khi đó ta có: $\left\{ \begin{array}{l}z_1^2 =  - 3 - 4i \Rightarrow \left| {z_1^2} \right| = \sqrt {{{\left( { - 3} \right)}^2} + {{\left( { - 4} \right)}^2}}  = 5\\z_2^2 =  - 3 + 4i \Rightarrow \left| {z_2^2} \right| = \sqrt {{{\left( { - 3} \right)}^2} + {4^2}}  = 5\end{array} \right.$.

Vậy $\left| {z_1^2} \right| + \left| {z_2^2} \right| = 5 + 5 = 10$.

Chọn A.

Phương pháp giải:

Gọi $z = a + bi\,\,\left( {a,\,\,b \in \mathbb{R}} \right) \Rightarrow \overline z  = a - bi.$

Từ biểu thức bài cho, tìm số phức $z$ sau đó thay số phức $z$ vừa tìm được vào các phương trình ở các đáp án để chọn đáp án đúng.

Hoặc giải các phương trình ở các đáp án đã cho, tìm phương trình chứa nghiệm là số phức $z$ đã tìm được ở trên.

Lời giải chi tiết:

Gọi $z = a + bi\,\,\left( {a,\,\,b \in \mathbb{R}} \right) \Rightarrow \overline z  = a - bi.$

Theo đề bài ta có: $z + 2\overline z  = 6 + i$

$\begin{array}{l} \Leftrightarrow a + bi + 2\left( {a - bi} \right) = 6 + i\\ \Leftrightarrow a + bi + 2a - 2bi = 6 + i\\ \Leftrightarrow 3a - bi = 6 + i\\ \Leftrightarrow \left\{ \begin{array}{l}3a = 6\\ - b = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b =  - 1\end{array} \right. \Rightarrow z = 2 - i.\end{array}$

+) Đáp án A: ${z^2} - 4z + 5 = 0 \Leftrightarrow \left[ \begin{array}{l}z = 2 + i\\z = 2 - i\end{array} \right.$

$\Rightarrow z = 2 - i$ là nghiệm của phương trình ${z^2} - 4z + 5 = 0$

Chọn A.

Phương pháp giải:

Giải phương trình đã cho trên tập số phức sau đó thay các nghiệm ${z_1},\,\,{z_2}$ vào các đáp án và chọn đáp án đúng.

Lời giải chi tiết:

Ta có: ${z^2} - 2z + 3 = 0$ $\Leftrightarrow {z^2} - 2z + 1 =  - 2$

$\Leftrightarrow {\left( {z - 1} \right)^2} = 2i$ $\Leftrightarrow \left[ \begin{array}{l}z - 1 = \sqrt 2 i\\z - 1 =  - \sqrt 2 i\end{array} \right.$$\Leftrightarrow \left[ \begin{array}{l}{z_1} = 1 + \sqrt 2 i\\{z_2} = 1 - \sqrt 2 i\end{array} \right.$

Khi đó ta có:

$+ )\,\,\left| {{z_1}} \right| = \sqrt {{1^2} + {{\left( {\sqrt 2 } \right)}^2}}  = \sqrt 3$ và $\left| {{z_2}} \right| = \sqrt {{1^2} + {{\left( { - \sqrt 2 } \right)}^2}}  = \sqrt 3$ $\Rightarrow \left| {{z_1}} \right| = \left| {{z_2}} \right| = \sqrt 3$

$\Rightarrow$ Đáp án A đúng.

$+ )\,\,{z_1}{z_2} = \left( {1 + \sqrt 2 i} \right)\left( {1 - \sqrt 2 i} \right)$ $= 1 - 2{i^2} = 1 + 2 = 3$$\Rightarrow$ Đáp án B đúng.

$+ )\,\,{z_1} + {z_2} = 1 + \sqrt 2 i + 1 - \sqrt 2 i = 2$ $\Rightarrow$ Đáp án C đúng.

$+ )\,\,\left| {{z_1}} \right| + \left| {{z_2}} \right| = \sqrt 3  + \sqrt 3$ $= 2\sqrt 3  \ne 2$$\Rightarrow$ Đáp án D sai.

Chọn D

Phương pháp giải:

- Tìm điều kiện để phương trình bậc hai có 2 nghiệm phức phân biệt: $\Delta  < 0$ hoặc $\Delta ' < 0$.

- Phương trình bậc hai có 2 nghiệm phức phân biệt thì hai số phức đó là hai số phức liên hợp nên luôn thỏa mãn điều kiện $\left| {{z_1}} \right| = \left| {{z_2}} \right|$.

Lời giải chi tiết:

Để phương trình có 2 nghiệm phức phân biệt thì $\Delta ' < 0$ $\Leftrightarrow {m^2} - 6m + 5 < 0 \Leftrightarrow 1 < m < 5$.

Phương trình bậc hai có 2 nghiệm phức phân biệt thì hai số phức đó là hai số phức liên hợp nên luôn thỏa mãn điều kiện $\left| {{z_1}} \right| = \left| {{z_2}} \right|$.

$\Rightarrow m \in \left( {1;5} \right)$. Mà $m \in \mathbb{Z} \Rightarrow m \in \left\{ {2;3;4} \right\}$. Vậy có 3 giá trị của $m$ thỏa mãn yêu cầu bài toán.

Chọn D.

Phương pháp giải:

- Tìm nghiệm phức của phương trình đã cho.

- Tìm số phức w rồi suy ra phần thực: Số phức $w = a + bi$ có phần thực là a.

Lời giải chi tiết:

Ta có ${z^2} - 4z + 5 = 0 \Leftrightarrow \left[ \begin{array}{l}z = 2 + i\\z = 2 - i\end{array} \right.$

Khi đó $w = z_1^2 + z_2^2 = {\left( {2 + i} \right)^2} + {\left( {2 - i} \right)^2} = 6$.

Vậy phần thực của số phức w là $a = 6$.

Chọn C.

Phương pháp giải:

- Giải phương trình bậc hai với hệ số thực tìm ${z_1},\,\,{z_2}$.

- Tính $\left| {{z_1}} \right|,\,\,\left| {{z_2}} \right|$ và thay vào tính giá trị biểu thức $\dfrac{1}{{\left| {{z_1}} \right|}} + \dfrac{1}{{\left| {{z_2}} \right|}}$, sử dụng công thức tính môđun của số phức $z = a + bi$$\Rightarrow \left| z \right| = \sqrt {{a^2} + {b^2}}$.

Lời giải chi tiết:

Ta có: $9{z^2} + 6z + 4 = 0 \Leftrightarrow \left[ \begin{array}{l}{z_1} =  - \dfrac{1}{3} + \dfrac{{\sqrt 3 }}{3}i\\{z_2} =  - \dfrac{1}{3} - \dfrac{{\sqrt 3 }}{3}i\end{array} \right.$.

$\Rightarrow \left| {{z_1}} \right| = \left| {{z_2}} \right| = \sqrt {\dfrac{1}{9} + \dfrac{1}{3}}  = \sqrt {\dfrac{4}{9}}  = \dfrac{2}{3}$.

Vậy $\dfrac{1}{{\left| {{z_1}} \right|}} + \dfrac{1}{{\left| {{z_2}} \right|}} = \dfrac{3}{2} + \dfrac{3}{2} = 3.$

Chọn B.

Phương pháp giải:

Sử dụng định lí Vi-ét: Phương trình bậc hai $a{z^2} + bz + c = 0\,\,\left( {a \ne 0} \right)$ có hai nghiệm phân biệt ${z_1},\,\,{z_2}$ thì $\left\{ \begin{array}{l}{z_1} + {z_2} =  - \dfrac{b}{a}\\{z_1}{z_2} = \dfrac{c}{a}\end{array} \right.$.

Lời giải chi tiết:

Phương trình $2{z^2} + 4z + 3 = 0$ có hai nghiệm phức ${z_1},\,\,{z_2}$ nên ta có: $\left\{ \begin{array}{l}{z_1} + {z_2} =  - 2\\{z_1}{z_2} = \dfrac{3}{2}\end{array} \right.$.

Khi đó ta có: $\left| {{z_1}{z_2} + i\left( {{z_1} + {z_2}} \right)} \right|$$\Leftrightarrow \left| { - \dfrac{3}{2} + i.\left( { - 2} \right)} \right| = \sqrt {{{\left( { - \dfrac{3}{2}} \right)}^2} + {{\left( { - 2} \right)}^2}}  = \dfrac{5}{2}$.

Chọn B.

Phương pháp giải:

Phương trình bậc hai $a{z^2} + bz + c = 0$ có nghiệm ${z_1},\,\,{z_2}$ thì $\left| {{z_1}} \right| = \left| {{z_2}} \right| = \dfrac{c}{a}$.

Lời giải chi tiết:

Gọi ${z_1},{z_2}$ là hai nghiệm phức của phương trình ${z^2} - 3z + 7 = 0$ $\Rightarrow \left| {{z_1}} \right| = \left| {{z_2}} \right| = \dfrac{c}{a} = \dfrac{7}{1} = 7$.

Vậy $T = \left| {z_1^2} \right| + \left| {z_2^2} \right| = 7 + 7 = 14.$

Chọn C.

Phương pháp giải:

Phương trình bậc hai $a{x^2} + bx + c = 0\,\,\left( {a \ne 0} \right)$ có 2 nghiệm không phải là số thực khi và chỉ khi $\Delta  < 0$.

Lời giải chi tiết:

Để phương trình ${z^2} + 2mz + 3m + 4 = 0$ có hai nghiệm không phải là số thực thì $\Delta ' < 0$.

$\Leftrightarrow {m^2} - 3m - 4 < 0 \Leftrightarrow  - 1 < m < 4$.

Mà $m \in \mathbb{Z} \Rightarrow m \in \left\{ {0;1;2;3} \right\}$.

Vậy có 4 giá trị của m thỏa mãn yêu cầu bài toán.

Chọn B.

Phương pháp giải:

Cách 1: Giải phương trình đã cho tìm ${z_1},\,\,{z_2}$ rồi tính biểu thức đề bài cho.

Cách 2: Áp dụng hệ thức Vi-et ta có: $\left\{ \begin{array}{l}{z_1} + {z_2} = 1\\{z_1}{z_2} = 1\end{array} \right..$

Theo đề bài ta có: $z_1^3 + z_2^3 = \left( {{z_1} + {z_2}} \right)\left[ {{{\left( {{z_1} + {z_2}} \right)}^2} - 3{z_1}{z_2}} \right]$ rồi tính modun hai vế.

Lời giải chi tiết:

Xét phương trình: ${z^2} - z + 1 = 0$

Áp dụng hệ thức Vi-et ta có: $\left\{ \begin{array}{l}{z_1} + {z_2} = 1\\{z_1}{z_2} = 1\end{array} \right..$

Theo đề bài ta có: $z_1^3 + z_2^3 = \left( {{z_1} + {z_2}} \right)\left[ {{{\left( {{z_1} + {z_2}} \right)}^2} - 3{z_1}{z_2}} \right]$

$\begin{array}{l} \Leftrightarrow z_1^3 + z_2^3 = 1\left( {{1^2} - 3} \right)\\ \Leftrightarrow z_1^3 + z_2^3 =  - 2\\ \Rightarrow \left| {z_1^3 + z_2^3} \right| = \left| { - 2} \right| = 2.\end{array}$

Chọn D.

Phương pháp giải:

- Giải phương trình bậc hai trên tập số phức tìm số phức ${z_0}$.

- Tính số phức $w = i{z_0}$.

- Điểm biểu diễn số phức $z = a + bi$ là $M\left( {a;b} \right)$.

Lời giải chi tiết:

Ta có: ${z^2} - 2z + 10 = 0 \Leftrightarrow \left[ \begin{array}{l}z = 1 + 3i\\z = 1 - 3i\end{array} \right.$.

Vì ${z_0}$ là nghiệm phức có phần ảo dương của của phương trình trên $\Rightarrow {z_0} = 1 + 3i$.

Khi đó ta có: $w = i{z_0} = i\left( {1 + 3i} \right) =  - 3 + i$.

Vậy điểm biểu diễn của số phức w là: $M\left( { - 3;1} \right).$

Chọn B.

Phương pháp giải:

Lời giải chi tiết:

Chọn A.

Phương pháp giải:

Xác định tổng và tích của hai số phức đã cho. Từ đó lập phương trình ${z^2} - Sz + P = 0$

Lời giải chi tiết:

$\left\{ \begin{array}{l}2 - 3i + 2 + 3i = 4\\\left( {2 - 3i} \right)\left( {2 + 3i} \right) = 13\end{array} \right. \Rightarrow 2 - 3i$ và $2 + 3i$ là nghiệm của phương trình ${z^2} - 4z + 13 = 0.$

Chọn: C

Phương pháp giải:

- Giải phương trình bậc hai tìm nghiệm phức của phương trình đã cho (Chú ý ${z_1}$có phần ảo âm).

- Suy ra ${z_1};\,\,{z_2}$ rồi tính số phức ${z_1} + 2{z_2}$ và kết luận phần ảo của nó.

Lời giải chi tiết:

Ta có: ${z^2} - 2z + 10 = 0 \Leftrightarrow \left[ \begin{array}{l}z = 1 + 3i\\z = 1 - 3i\end{array} \right.$.

Vì ${z_1}$có phần ảo âm nên ta có ${z_1} = 1 - 3i,\,\,{z_2} = 1 + 3i$.

Khi đó ${z_1} + 2{z_2} = 1 - 3i + 2\left( {1 + 3i} \right)$$= 3 + 3i$.

Vậy số phức ${z_1} + 2{z_2}$ có phần thực và phần ảo lần lượt là $3;\,\,3$.

Chọn C.

Phương pháp giải:

- Giải phương trình bậc hai tìm ${z_1},\,\,{z_2}$.

- Tìm các điểm $M,\,\,N$. Điểm biểu diễn số phức $z = a + bi$ là $M\left( {a;b} \right)$.

- Tính độ dài đoạn thẳng $MN = \sqrt {{{\left( {{x_N} - {x_M}} \right)}^2} + {{\left( {{y_N} - {y_M}} \right)}^2} + {{\left( {{z_N} - {z_M}} \right)}^2}}$.

Lời giải chi tiết:

Ta có: ${z^2} - 4z + 9 = 0 \Leftrightarrow \left[ \begin{array}{l}{z_1} = 2 + \sqrt 5 i\\{z_2} = 2 - \sqrt 5 i\end{array} \right.$.

$\Rightarrow M\left( {2;\sqrt 5 } \right)$ và $N\left( {2; - \sqrt 5 } \right)$.

Vậy $MN = \sqrt {{{\left( {2 - 2} \right)}^2} + {{\left( { - \sqrt 5  - \sqrt 5 } \right)}^2}}  = \sqrt {20}  = 2\sqrt 5$.

Chọn C.

Phương pháp giải:

- Giải phương trình tìm ${z_1},\,\,{z_2}$.

- Số phức $z = a + bi$ có số phức liên hợp $\overline z  = a - bi$.

Lời giải chi tiết:

Ta có:

${z^2} + 9 = 0 \Leftrightarrow {z^2} =  - 9 \Leftrightarrow \left[ \begin{array}{l}{z_1} = 3i\\{z_2} =  - 3i\end{array} \right.$ $\Leftrightarrow \left[ \begin{array}{l}\overline {{z_1}}  =  - 3i\\\overline {{z_2}}  = 3i\end{array} \right. \Rightarrow \overline {{z_1}}  + \overline {{z_2}}  = 0$.

Chọn D.

Phương pháp giải:

- Tìm nghiệm của phương trình đã cho.

- Sử dụng dữ kiện để tìm ${z_1};\,\,{z_2}$ rồi tính số phức w.

Lời giải chi tiết:

Ta có ${z^2} - 2z + 5 = 0 \Leftrightarrow \left[ \begin{array}{l}z = 1 + 2i\\z = 1 - 2i\end{array} \right.$

Mà ${z_1} - {z_2}$ có phần ảo là số thực âm nên $\left\{ \begin{array}{l}{z_1} = 1 - 2i\\{z_2} = 1 + 2i\end{array} \right..$

$\Rightarrow {\rm{w}} = 2z_1^2 - z_2^2 =  - 3 - 12i$.

Vậy phần ảo của số phức w là $- 12.$

Chọn B.

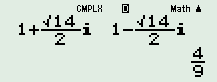
Phương pháp giải:

Tìm hai nghiệm phức của phương trình từ đó suy ra giá trị của P.

Lời giải chi tiết:

Ta có: $2{x^2} - 4x + 9 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 + \dfrac{{\sqrt {14} }}{2}i = z\\x = 1 - \dfrac{{\sqrt {14} }}{2}i = w\end{array} \right.$ . 

Khi đó $P = \dfrac{1}{z} + \dfrac{1}{{\rm{w}}} = \dfrac{1}{{1 + \dfrac{{\sqrt {14} }}{2}i}} + \dfrac{1}{{1 - \dfrac{{\sqrt {14} }}{2}i}} = \dfrac{4}{9}.$

Chọn C.

Phương pháp giải:

Giải phương trình bậc hai trên tập số phức.

Lời giải chi tiết:

Ta có: ${z^2} - 2z + 3 = 0 \Leftrightarrow z = 1 \pm \sqrt 2 i$

Do ${z_1}$ là nghiệm phức có phần ảo dương nên ${z_1} = 1 + \sqrt 2 i \Rightarrow i{z_1} = i - \sqrt 2$: có phần thực bằng $- \sqrt 2$.

Chọn: C

Phương pháp giải:

Nghiệm phức của phương trình bậc hai hệ số thực trên tập số phức là hai số phức liên hợp.

Lời giải chi tiết:

Do $z =  - 3 + 4i$ là một nghiệm của ${z^2} + az + b = 0$ với $a,\,\,b \in \mathbb{R}$ nên $\overline z  =  - 3 - 4i$ cũng là nghiệm của phương trình.

Áp dụng định lí Vi-ét ta có: $\left\{ \begin{array}{l}z + \overline z  =  - a\\z\overline z  = b\end{array} \right. \Rightarrow \left\{ \begin{array}{l} - a =  - 6\\b = 25\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 6\\b = 25\end{array} \right. \Rightarrow a - b =  - 19$.

Chọn D.

Phương pháp giải:

Giải phương trình bậc hai ẩn $z$ sau đó sử dụng công thức nhân số phức để tính $i{z_0}.$

Lời giải chi tiết:

${z^2} + 2z + 10 = 0 \Leftrightarrow \left[ \begin{array}{l}z =  - 1 + 3i\\z =  - 1 - 3i\end{array} \right. \Rightarrow {z_0} =  - 1 + 3i$ do số phức có phần ảo dương.

$\Rightarrow i{z_0} = i\left( { - 1 + 3i} \right) =  - i + 3{i^2} =  - 3 - i.$

Chọn  C.

Phương pháp giải:

Số tập con của tập có $n$ phần tử là ${2^n}.$

Lời giải chi tiết:

Phương trình ${z^2} + z + 1 = 0$ là phương trình bậc 2 trên tập số phức nên luôn có 2 nghiệm.

Suy ra tập $S$ có hai phần tử nên số tập con của $S$ là ${2^2} = 4.$

Chọn D

Phương pháp giải:

Giải phương trình đã cho tìm hai số phức ${z_1},\,\,{z_2}$  rồi tính modul của số phức đề bài yêu cầu.

Lời giải chi tiết:

Ta có: ${z^2} - 2z + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}{z_1} = 1 + \sqrt 2 i \Rightarrow \left| {{z_1}} \right| = \sqrt {1 + 2}  = \sqrt 3 \\{z_2} = 1 - \sqrt 2 i \Rightarrow \left| {{z_2}} \right| = \sqrt {1 + 2}  = \sqrt 3 \end{array} \right..$

$\Rightarrow \left| {z_1^3.z_2^4} \right| = {\left| {{z_1}} \right|^3}.{\left| {{z_2}} \right|^4} = {\left( {\sqrt 3 } \right)^3}.{\left( {\sqrt 3 } \right)^4} = {\left( {\sqrt 3 } \right)^7} = 27\sqrt 3 .$

Chọn  C.

Phương pháp giải:

+) Giải phương trình tìm ${z_1};\,\,{z_2}$.

+) Thay ${z_1};\,\,{z_2}$ vào tính $w$.

Lời giải chi tiết:

${z^2} + 4z + 5 = 0 \Leftrightarrow \left\{ \begin{array}{l}{z_1} =  - 2 + i\\{z_2} =  - 2 - i\end{array} \right.$

$\begin{array}{l}w = {\left( {1 + {z_1}} \right)^{100}} + {\left( {1 + {z_2}} \right)^{100}} = {\left( {1 - 2 + i} \right)^{100}} + {\left( {1 - 2 - i} \right)^{100}}\\\,\,\,\,\, = {\left( {i - 1} \right)^{100}} + {\left( { - 1 - i} \right)^{100}} = {\left( {i - 1} \right)^{100}} + {\left( {i + 1} \right)^{100}}\\\,\,\,\, = {\left( {{{\left( {i - 1} \right)}^2}} \right)^{50}} + {\left( {{{\left( {i + 1} \right)}^2}} \right)^{50}} = {\left( { - 2i} \right)^{50}} + {\left( {2i} \right)^{50}}\\\,\,\,\, = {2.2^{50}}.{i^{50}} = {2^{51}}.{\left( {{i^4}} \right)^{12}}.{i^2} = {2^{51}}.1.\left( { - 1} \right) =  - {2^{51}}\end{array}$

Chọn: B

Phương pháp giải:

Xét với điều kiện của $a > 2,$ giải phương trình bậc hai ẩn $z.$  

Lời giải chi tiết:

Ta có: $\Delta ' = 1 - a.$

$\Rightarrow$ Với mọi $a > 2 \Rightarrow \Delta  < 0 \Rightarrow$ Phương trình đã cho luôn có hai nghiệm phức và hai nghiệm phức này thỏa mãn ${z_2} = \overline {{z_1}} .$

Giả sử: ${z_1} = x + yi \Rightarrow {z_2} = x - yi.$

$\Rightarrow {z_1} + {z_2} = 2x \Rightarrow$ đáp án A đúng.

    ${z_1} - {z_2} = 2yi \Rightarrow$ đáp án B đúng.

$\dfrac{{{z_1}}}{{{z_2}}} + \dfrac{{{z_2}}}{{{z_1}}} = \dfrac{{z_1^2 + z_2^2}}{{{z_1}{z_2}}} = \dfrac{{{{\left( {x + yi} \right)}^2} + {{\left( {x - yi} \right)}^2}}}{{\left( {x + yi} \right)\left( {x - yi} \right)}} = \dfrac{{2{x^2} - 2{y^2}}}{{{x^2} + {y^2}}} \Rightarrow$ đáp án D đúng.

Chọn C.

Phương pháp giải:

Áp dụng hệ thức Vi – ét.

Lời giải chi tiết:

${z_1},{z_2}$ là nghiệm của phương trình ${z^2} - 2z + 4 = 0 \Rightarrow \left\{ \begin{array}{l}{z_1} + {z_2} = 2\\{z_1}{z_2} = 4\end{array} \right.$

$P = \dfrac{{z_1^2}}{{{z_2}}} + \dfrac{{z_2^2}}{{{z_1}}} = \dfrac{{z_1^3 + z_2^3}}{{{z_1}{z_2}}} = \dfrac{{{{\left( {{z_1} + {z_2}} \right)}^3} - 3{z_1}{z_2}\left( {{z_1} + {z_2}} \right)}}{{{z_1}{z_2}}} = \dfrac{{{2^3} - 3.4.2}}{4} =  - 4$.

Chọn: C

Phương pháp giải:

Áp dụng định lý Vi-et cho phương trình bậc hai $\left\{ \begin{array}{l}{z_1} + {z_2} =  - \frac{b}{a}\\{z_1}{z_2} = \frac{c}{a}\end{array} \right.$

Lời giải chi tiết:

Áp dụng định lí Vi – et cho phương trình ${z^2} - mz + 2m - 1 = 0$ trong tập số phức ta có: $\left\{ \begin{array}{l}{z_1} + {z_2} =  - \frac{b}{a} = m\\{z_1}{z_2} = \frac{c}{a} = 2m - 1\end{array} \right.$

Khi đó: $z_1^2 + z_2^2 =  - 10 \Leftrightarrow {\left( {{z_1} + {z_2}} \right)^2} - 2{z_1}{z_2} =  - 10$ $\Leftrightarrow {m^2} - 2\left( {2m - 1} \right) =  - 10 \Leftrightarrow {m^2} - 4m + 12 = 0 \Leftrightarrow m = 2 \pm 2\sqrt 2 i$

Chọn B.

Phương pháp giải:

Tìm ${z_1},\,\,{z_2}$, thay vào biểu thức ${({z_1} - 1)^{2018}} + {({z_2} - 1)^{2018}}$ và tính giá trị của biểu thức đó.

Lời giải chi tiết:

${z^2} - 4z + 5 = 0 \Leftrightarrow \left[ \begin{array}{l}{z_1} = 2 + i\\{z_2} = 2 - i\end{array} \right.$

$\begin{array}{l}\,\,\,\,\,{({z_1} - 1)^{2018}} + {({z_2} - 1)^{2018}}\\ = {(2 + i - 1)^{2018}} + {(2 - i - 1)^{2018}}\\ = {(1 + i)^{2018}} + {(1 - i)^{2018}}\\ = {\left( {{{(1 + i)}^2}} \right)^{1009}} + {\left( {{{(1 - i)}^2}} \right)^{1009}}\\ = {\left( {2i} \right)^{1009}} + {\left( { - 2i} \right)^{1009}}\\ = {2^{2009}}.{i^{20019}} - {2^{2009}}.{i^{1009}} = 0\end{array}$

Chọn: C

Phương pháp giải:

Tìm tổng $S=z+\overline{z}$ và tích $P=z.\overline{z}$, khi đó $z;\overline{z}$ là nghiệm của phương trình ${{Z}^{2}}-SZ+P=0$.

Lời giải chi tiết:

$\overline{z}=a-bi\Rightarrow z+\overline{z}=2a;\,\,z.\overline{z}={{a}^{2}}+{{b}^{2}}\Rightarrow z;\overline{z}$ là nghiệm của phương trình ${{z}^{2}}-2az+{{a}^{2}}+{{b}^{2}}=0$.

Chọn B.

Phương pháp giải:

 Cách 1: Giải các phương trình bậc hai ẩn z ở các đáp án, đáp án nào có nghiệm $z=1+2i$ thì chọn đáp án đó.

Cách 2: Thay nghiệm $z=1+2i$ vào các phương trình ở các đáp án. Đáp án nào thỏa mãn thì chọn đáp án đó. 

Lời giải chi tiết:

 +) Xét phương trình: ${z^2} - 2z + 3 = 0 \Leftrightarrow {z^2} - 2z + 1 + 2 = 0 \Leftrightarrow {\left( {z - 1} \right)^2} =  - 2 \Leftrightarrow {\left( {z - 1} \right)^2} = 2{i^2}$

$\Leftrightarrow \left| {z - 1} \right| = \sqrt 2 i \Leftrightarrow \left[\begin{array}{l}z - 1 = \sqrt 2 i\\z - 1 = - \sqrt 2 i \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}z = 1 + \sqrt 2 i\\z = 1 - \sqrt 2 i \end{array} \right. \Rightarrow$ loại đáp án A.

+) Xét phương trình: ${{z}^{2}}+2z+5=0\Leftrightarrow {{z}^{2}}+2z+4+1=0\Leftrightarrow {{\left( z+2 \right)}^{2}}=-1={{i}^{2}}$ 

$\Leftrightarrow \left| {z + 2} \right| = i \Leftrightarrow \left[ \begin{array}{l} z + 2 = i\\ z + 2 = - i \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} z = - 2 + i\\ z = - 2 - i \end{array} \right. \Rightarrow$loại đáp án B.

+) Xét phương trình: ${{z}^{2}}-2z+5=0\Leftrightarrow {{z}^{2}}-2z+1+4=0\Leftrightarrow {{\left( z-1 \right)}^{2}}=-4=-4{{i}^{2}}$ 

$\Leftrightarrow \left| {z - 1} \right| = 2i \Leftrightarrow \left[ \begin{array}{l} z - 1 = 2i\\ z - 1 = - 2i \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} z = 1 + 2i\\ z = 1 - 2i \end{array} \right. \Rightarrow$ chọn đáp án C.

Chọn C.

Phương pháp giải:

Biến đổi phương trình trở thành phương trình bậc hai.

Giải phương trình bậc hai, kết hợp điều kiện để loại nghiệm.

Lời giải chi tiết:

Phương trình: $\frac{4z-3-7i}{z-i}=z-2i$ (điều kiện $z\ne i$)

                      $\begin{array}{l}\Leftrightarrow 4z - 3 - 7i = (z - 2i)(z - i)\\ \Leftrightarrow 4z - 3 - 7i = {z^2} - iz - 2iz + 2{i^2}\\ \Leftrightarrow {z^2} - (4 + 3i)z + 1 + 7i = 0\end{array}$

Có: $\Delta ={{\left( 4+3i \right)}^{2}}-4(1+7i)=16+24i+9{{i}^{2}}-4-28i$

           $=3-4i=4-2.2i+{{i}^{2}}={{\left( 2-i \right)}^{2}}$

$\Rightarrow \sqrt{\Delta }=\sqrt{{{\left( 2-i \right)}^{2}}}=\left| 2-i \right|$

 $\Rightarrow$ Phương trình có $2$  nghiệm là: ${{z}_{1}}=\frac{4+3i+2-i}{2}=3+i;{{z}_{2}}=\frac{4+3i-2+i}{2}=1+2i$(thỏa mãn)

Chọn D

Phương pháp giải:

Phương pháp giải phương trình bậc hai trên tập số phức: $a{{x}^{2}}+bx+c=0\left( a\ne 0,a,b,c\in R \right)$

- Tính $\Delta ={{b}^{2}}-4ac$.

+ $\Delta >0$ thì phương trình có hai nghiệm thực phân biệt ${{x}_{1,2}}=\frac{-b\pm \sqrt{\Delta }}{2a}$.

+ $\Delta =0$ thì phương trình có nghiệm kép ${{x}_{1,2}}=-\frac{b}{2a}$.

+ $\Delta <0$ thì phương trình có hai nghiệm phức phân biệt ${{x}_{1,2}}=\frac{-b\pm i\sqrt{-\Delta }}{2a}$.

Lời giải chi tiết:

1) Sai vì nếu $\Delta <0$ thì $\sqrt{\Delta }=\pm i\sqrt{\left| \Delta  \right|}$ do đó phương trình có $2$  nghiệm phức

2) Đúng

3) Đúng

Vậy có $2$  mệnh đề đúng

Chọn C

Phương pháp giải:

Phương pháp giải phương trình bậc hai trên tập số phức: $a{{x}^{2}}+bx+c=0\left( a\ne 0,a,b,c\in C \right)$

- Tính $\Delta ={{b}^{2}}-4ac$.

- Tìm một căn bậc hai của $\Delta$.

- Áp dụng công thức nghiệm ${{x}_{1,2}}=\frac{-b\pm \sqrt{\Delta }}{2a}$.

Tính nghiệm $z$ thỏa mãn đề bài rồi tính $a,b$.

Lời giải chi tiết:

Phương trình: ${{z}^{2}}+\left( 1+2i \right)z-17+19i=0$

Có: $\Delta ={{\left( 1+2i \right)}^{2}}-4(-17+19i)=1+4i+4{{i}^{2}}+68-76i$

            $=65-72i=81-2.9.4i+16{{i}^{2}}={{\left( 9-4i \right)}^{2}}$

       $\Rightarrow \sqrt{\Delta }=\sqrt{{{\left( 9-4i \right)}^{2}}}=\left| 9-4i \right|$

$\Rightarrow$Phương trình có $2$ nghiệm: ${{z}_{1}}=\frac{-1-2i+9-4i}{2}=4-3i$ (thỏa mãn), ${{z}_{2}}=\frac{-1-2i-9+4i}{2}=-5+i$(loại)

Do đó: ${z^2} = a + bi \Leftrightarrow {\left( {4 - 3i} \right)^2} = a + bi \Leftrightarrow 16 - 24i + 9{i^2} = a + bi \Leftrightarrow \left\{ \begin{array}{l}a = 7\\b =  - 24\end{array} \right. \Rightarrow a.b{\rm{ }} =  - 168$

Chọn A

Phương pháp giải:

Phương pháp. Kiểm tra trực tiếp từng kết luận.

Lời giải chi tiết:

Lời giải chi tiết.

Với $a\ne 0$ ta có phương trình $a{{z}^{2}}+bz+c=0$ (*)  là phương trình bậc hai ẩn z có $\Delta ={{b}^{2}}-4ac.$

Xét trong tập số phức thì phương trình  (*) luôn có nghiệm $\Rightarrow$ D đúng.

Áp dụng hệ thức Vi-et ta có: ${{z}_{1}}+{{z}_{2}}=-\frac{b}{a}.$

$\Rightarrow$ Khi $b=0$ ta có: ${{z}_{1}}+{{z}_{2}}=0\Rightarrow$ A đúng.

+) Xét $\Delta <0$ ta có phương trình (*) có hai nghiệm phức phân biệt: $\left[ \begin{align} & {{z}_{1}}=\frac{-b+i\sqrt{\left| \Delta  \right|}}{2a} \\ & {{z}_{2}}=\frac{-b-i\sqrt{\left| \Delta  \right|}}{2a} \\ \end{align} \right.$

$\Rightarrow \left| {{z}_{1}} \right|=\left| {{z}_{2}} \right|\Rightarrow$ B đúng.

+) Xét $\Delta >0\Rightarrow$ phương trình (*) có hai nghiệm thực phân biệt: $\left[ \begin{align} & {{z}_{1}}=\frac{-b+\sqrt{\Delta }}{2a} \\  & {{z}_{2}}=\frac{-b-\sqrt{\Delta }}{2a} \\ \end{align} \right.\Rightarrow$ C sai.

Chọn C.

Lời giải chi tiết:

$\begin{array}{l}{z^4}-{z^2}-2 = 0 \Leftrightarrow \left( {{z^2} + 1} \right)({z^2} - 2) = 0\\ \Leftrightarrow \left[ \begin{array}{l}{z^2} + 1 = 0\\{z^2} - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{z^2} = - 1 = {i^2}\\{z^2} = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}z = \pm i\\z = \pm \sqrt 2 \end{array} \right.\end{array}$

Vậy tập nghiệm của phương trình là: $\left\{ { \pm \sqrt 2 ; \pm i} \right\}$

Chọn B

Lời giải chi tiết:

$\begin{array}{l}{z^4}-1 = 0 \Leftrightarrow \left( {{z^2} + 1} \right)({z^2} - 1) = 0\\ \Leftrightarrow \left[ \begin{array}{l}{z^2} + 1 = 0\\{z^2} - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{z^2} = - 1 = {i^2}\\{z^2} = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}z = \pm i\\z = \pm 1\end{array} \right.\end{array}$

Vậy tập nghiệm của phương trình là: $\left\{ { \pm 1; \pm i} \right\}$

Chọn C

Lời giải chi tiết:

$\begin{array}{l}{z^4} - 2{z^2} - 8 = 0 \Leftrightarrow \left( {{z^2} + 2} \right)({z^2} - 4) = 0\\ \Leftrightarrow \left[ \begin{array}{l}{z^2} + 2 = 0\\{z^2} - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{z^2} = - 2 = 2{i^2}\\{z^2} = 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}z = \pm i\sqrt 2 \\z = \pm 2\end{array} \right.\end{array}$

Giả sử: ${z_1} = i\sqrt 2 ;{z_2} =  - i\sqrt 2 ;{z_3} = 2;{z_4} =  - 2$

$\Rightarrow P = \left| {{z_1}} \right|.\left| {{z_2}} \right|.\left| {{z_3}} \right|.\left| {{z_4}} \right| = \left| {i\sqrt 2 } \right|.\left| { - i\sqrt 2 } \right|.\left| 2 \right|.\left| { - 2} \right| = 8$

Chọn B

Lời giải chi tiết:

$\begin{array}{l}{z^3} + 1 = 0 \Leftrightarrow \left( {z + 1} \right)\left( {{z^2} - z + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}z + 1 = 0\\{z^2} - z + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}z = - 1\\{z^2} - z + 1 = 0\end{array} \right.\end{array}$

+) Phương trình: $z^2 – z + 1 = 0$ có $\Delta = 1 – 4 = -3 = 3i^2$

                        $\Rightarrow z = \dfrac{{1 + i\sqrt 3 }}{2};z = \dfrac{{1 - i\sqrt 3 }}{2}$

Vậy tập nghiệm của phương trình là: $\left\{ { - 1;\dfrac{{1 + i\sqrt 3 }}{2};\dfrac{{1 - i\sqrt 3 }}{2}} \right\}$

Chọn B

Phương pháp giải:

Lời giải chi tiết:

$\left( {{z^2} + i} \right)\left( {{z^2} - 2iz - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{z^2} + i = 0\\{z^2} - 2iz - 1 = 0\end{array} \right.$

+) Phương trình ${z^2} + i = 0 \Rightarrow {z^2} =  - i \Rightarrow$ z là một căn bậc hai của $-i$.

Gọi $z = a + bi$ là một căn bậc hai của $-i$ ta có  

$\begin{array}{l}{z^2} = - i \Leftrightarrow {a^2} + 2abi - {b^2} = - i\\\Rightarrow \left\{ \begin{array}{l}{a^2} - {b^2} = 0\\2ab = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}a = b\\a = - b\end{array} \right.\\2ab = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2{a^2} = - 1\,\,\left( {vn} \right)\\2{a^2} = 1\end{array} \right. \Rightarrow \left[ \begin{array}{l}a = \frac{1}{{\sqrt 2 }} \Rightarrow b = - \frac{1}{{\sqrt 2 }}\\a = - \frac{1}{{\sqrt 2 }} \Rightarrow b = \frac{1}{{\sqrt 2 }}\end{array} \right. \Rightarrow \left[ \begin{array}{l}z = \frac{1}{{\sqrt 2 }} - \frac{1}{{\sqrt 2 }}i\\z = - \frac{1}{{\sqrt 2 }} + \frac{1}{{\sqrt 2 }}i\end{array} \right.\end{array}$

$\Rightarrow$ Phương trình trên có hai nghiệm.

+) Phương trình: ${z^2}-2iz-1 = 0 \Leftrightarrow {z^2}-2iz + {i^2} = 0 \Leftrightarrow {\left( {z-i} \right)^2} = 0 \Leftrightarrow z = i$

Vậy phương trình có 3 nghiệm.

Chọn D