Phương pháp giải:

Khoảng cách từ \(M\left( {{x_0};{y_0};{z_0}} \right)\) đến mặt phẳng \(\left( {Oxy} \right)\) là: \(\left| {{z_0}} \right|\)

Lời giải chi tiết:

Khoảng cách từ \(M\left( {1;2;--3} \right)\) đến mặt phẳng \(\left( {Oxy} \right)\) bằng 3.

Chọn B.

Phương pháp giải:

- Nếu \(\overrightarrow a  \bot \left( P \right)\) thì vecto \(\overrightarrow a \)  là một vecto pháp tuyến của mặt phẳng \(\left( P \right)\)

- Vecto \(\overrightarrow a \)  là một vecto pháp tuyến của mặt phẳng \(\left( P \right)\)thì vecto \(k\overrightarrow a \,\,\left( {k \ne 0} \right)\) cũng là vecto pháp tuyến của mặt phẳng \(\left( P \right)\)

Lời giải chi tiết:

Vì \(M'\) là hình chiếu vuông góc của \(M\) lên mp\(\left( \alpha  \right)\) nên \(M'M \bot \left( \alpha  \right)\)

Do đó, \(\overrightarrow {MM'} \) là một vecto pháp tuyến của mặt phẳng \(\left( \alpha  \right).\)

Suy ra mặt phẳng \(\left( \alpha  \right)\) có một vecto pháp tuyến là : \(\overrightarrow {MM'}  = \left( {4;2;6} \right).\)

Vậy, mặt phẳng \(\left( \alpha  \right)\) cũng có một vecto pháp tuyến \(\overrightarrow n  = \dfrac{1}{2}\overrightarrow {MM'}  = \left( {2;1;3} \right).\)  

Chọn C.

Phương pháp giải:

- Tìm tọa độ các điểm \(A,\,\,B,\,\,C\).

   + Hình chiếu của \(M\left( {{x_0};{y_0};{z_0}} \right)\) lên trục \(Ox\) là \(A\left( {{x_0};0;0} \right)\).

   + Hình chiếu của \(M\left( {{x_0};{y_0};{z_0}} \right)\) lên trục \(Oy\) là \(B\left( {0;{y_0};0} \right)\).

   + Hình chiếu của \(M\left( {{x_0};{y_0};{z_0}} \right)\) lên trục \(Oz\) là \(C\left( {0;0;{x_0}} \right)\).

- Viết phương trình mặt phẳng \(\left( {ABC} \right)\) đi qua \(A,\,\,B,\,\,C\) dạng mặt chắn: Mặt phẳng đi qua các điểm \(A\left( {{x_0};0;0} \right)\), \(B\left( {0;{y_0};0} \right)\), \(C\left( {0;0;{x_0}} \right)\) có phương trình \(\dfrac{x}{{{x_0}}} + \dfrac{y}{{{y_0}}} + \dfrac{z}{{{z_0}}} = 1\).

- Tìm mặt phẳng song song với mặt phẳng \(\left( {ABC} \right)\): Hai mặt phẳng song song khi VTPT của chúng là các vectơ cùng phương.

Lời giải chi tiết:

\(M\left( { - 3;\,\,2;\,\,4} \right)\). Theo giả thiết, \(A,\,\,B,\,\,C\) là hình chiếu vuông góc của \(M\) lên trục \(Ox,\,\,Oy,\,\,Oz\) nên \(A\left( { - 3;\,0;\,0} \right);\,\,B\left( {0;\,2;\,0} \right);\,\,C\left( {0;\,0;\,4} \right).\)

Suy ra phương trình mặt phẳng \(\left( {ABC} \right)\) dạng mặt chắn là: \(\dfrac{x}{{ - 3}} + \dfrac{y}{2} + \dfrac{z}{4} = 1 \Leftrightarrow 4x - 6y - 3z + 12 = 0\).

Trong các mặt phẳng đã cho, mặt phẳng song song với mặt phẳng \(\left( {ABC} \right)\) có phương trình là \(4x - 6y - 3z - 12 = 0\).

Chọn C.

Phương pháp giải:

- \(A,\,\,B \in \left( \alpha  \right) \Rightarrow AB \subset \left( \alpha  \right) \Rightarrow \overrightarrow {{n_\alpha }}  \bot \overrightarrow {AB} \), \(\left( \alpha  \right) \bot \left( P \right) \Rightarrow \overrightarrow {{n_P}}  \bot \overrightarrow {{n_\alpha }} \).

- \(\overrightarrow {{n_\alpha }}  = \left[ {\overrightarrow {AB} ;\overrightarrow {{n_P}} } \right]\).

- Phương trình mặt phẳng đi qua \(M\left( {{x_0};{y_0};{z_0}} \right)\) và có 1 VTPT \(\overrightarrow n \left( {A;B;C} \right)\) có phương trình là:

\(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\)

Lời giải chi tiết:

Ta có \(A\left( { - 2;3; - 1} \right);\,\,B\left( {1; - 2; - 3} \right)\)\( \Rightarrow \overrightarrow {AB}  = \left( {3; - 5; - 2} \right).\)

Mặt phẳng \(\left( P \right):3x - 2y + z + 9 = 0\) có 1 vecto pháp tuyến là \(\overrightarrow {{n_P}}  = \left( {3; - 2;1} \right)\).

\( \Rightarrow \left[ {\overrightarrow {AB} ;\overrightarrow {{n_P}} } \right] = \left( { - 9; - 9;9} \right)\).

Vì \(\left\{ \begin{array}{l}AB \subset \left( \alpha  \right)\\\left( \alpha  \right) \bot \left( P \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\overrightarrow {{n_\alpha }}  \bot \overrightarrow {AB} \\\overrightarrow {{n_\alpha }}  \bot \overrightarrow {{n_P}} \end{array} \right.\) \( \Rightarrow \left( \alpha  \right)\) nhận \(\left[ {\overrightarrow {AB} ;\overrightarrow {{n_P}} } \right] = \left( { - 9; - 9;9} \right)\) là 1 VTPT \( \Rightarrow \overrightarrow {{n_\alpha }} \left( {1;1; - 1} \right)\) cũng là 1 VTPT của mặt phẳng \(\left( \alpha  \right)\).

Vậy phương trình mặt phẳng \(\left( \alpha  \right)\) là: \(1\left( {x + 2} \right) + 1\left( {y - 3} \right) - 1\left( {z + 1} \right) = 0\) \( \Leftrightarrow x + y - z - 2 = 0.\)

Chọn A.

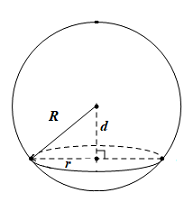
Phương pháp giải:

- Mặt cầu \(\left( S \right)\) tâm \(I\) tiếp xúc với \(\left( P \right)\) có bán kính \(R = d\left( {I;\left( P \right)} \right)\).

- Khoảng cách từ \(I\left( {a;b;c} \right)\) đến mặt phẳng \(\left( P \right):\,\,Ax + By + Cz + D = 0\) là: \(d\left( {I;\left( P \right)} \right) = \dfrac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).

- Mặt cầu tâm \(I\left( {a;b;c} \right)\) bán kính \(R\) là \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\).

Lời giải chi tiết:

Mặt cầu \(\left( S \right)\) tâm \(I\) tiếp xúc với \(\left( P \right)\) có bán kính \(R = d\left( {I;\left( P \right)} \right)\).

\( \Rightarrow R = d\left( {I;\left( P \right)} \right) = \dfrac{{\left| { - 1 - 2.2 - 2.1 - 2} \right|}}{3} = 3.\)

Mặt cầu \(\left( S \right)\) có tâm \(I\left( { - 1;2;1} \right)\), bán kính \(R = 3\) có phương trình là:

\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 1} \right)^2} = 9.\)

Chọn C.

Phương pháp giải:

- Khoảng cách từ \(M\left( {{x_0};{y_0};{z_0}} \right)\) đến \(\left( P \right):\,\,Ax + By + Cz + D = 0\) là: \(d\left( {M;\left( P \right)} \right) = \dfrac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).

- Mặt cầu \(\left( S \right)\) tâm \(I\), bán kính \(R\) cắt \(\left( P \right)\) theo một đường tròn bán kính \(r\) thì \({R^2} = {d^2} + {r^2}\) trong đó \(d = d\left( {I;\left( P \right)} \right)\).

- Mặt cầu tâm \(I\left( {{x_0};{y_0};{z_0}} \right)\), bán kính \(R\) có phương trình \({\left( {x - {x_0}} \right)^2} + {\left( {y - {y_0}} \right)^2} + {\left( {z - {z_0}} \right)^2} = {R^2}.\)

Lời giải chi tiết:

Ta có: \(d\left( {I;\left( P \right)} \right) = \dfrac{{\left| {2.1 - 2 + 2.\left( { - 1} \right) - 1} \right|}}{{\sqrt {{2^2} + {{\left( { - 1} \right)}^2} + {2^2}} }} = 1 = d\).

\( \Rightarrow \) Bán kính của mặt cầu là \(R = \sqrt {{r^2} + {d^2}}  = \sqrt {8 + 1}  = 3\).

Vậy phương trình mặt cầu cần tìm là: \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 9.\)

Chọn B.

Phương pháp giải:

Mặt phẳng song song với trục \(Oy\) có VTPT vuông góc với \(\overrightarrow j \left( {0;1;0} \right)\).

Lời giải chi tiết:

Xét mặt phẳng bất kì \(\left( P \right):\,\,Ax + By + Cz + D = 0\) có 1 VTPT là \(\overrightarrow n \left( {A;B;C} \right)\).

Để mặt phẳng này song song với \(Oy\) thì \(\overrightarrow n .\overrightarrow j  = 0\) với \(\overrightarrow j \left( {0;1;0} \right)\) là 1 VTCP của \(Oy\).

\( \Rightarrow A.0 + B.1 + C.0 = 0 \Leftrightarrow B = 0\) \( \Rightarrow \overrightarrow n \left( {A;0;C} \right)\).

Lại có \(Oy\parallel \left( P \right) \Rightarrow O \notin \left( P \right) \Rightarrow D \ne 0\).

Trong 4 đáp án ta thấy mặt phẳng \(\left( \alpha  \right):x - 3z + 4 = 0.\)thỏa mãn điều kiện trên.

Chọn D.

Phương pháp giải:

- Tìm trọng tâm \(G\) tam giác \(ABC\): \(\left\{ \begin{array}{l}{x_G} = \dfrac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \dfrac{{{y_A} + {y_B} + {y_C}}}{3}\\{z_G} = \dfrac{{{z_A} + {z_B} + {z_C}}}{3}\end{array} \right.\).

- Hình chiếu của \(G\left( {a;b;c} \right)\) lên các trục \(Ox,\,\,Oy,\,\,Oz\) lần lượt là \(M\left( {a;0;0} \right)\), \(N\left( {0;b;0} \right)\), \(P\left( {0;0;c} \right)\).

- Mặt phẳng đi qua \(M\left( {a;0;0} \right)\), \(N\left( {0;b;0} \right)\), \(P\left( {0;0;c} \right)\) có dạng \(\dfrac{x}{a} + \dfrac{y}{b} + \dfrac{z}{c} = 1\) (phương trình mặt chắn).

Lời giải chi tiết:

Gọi \(G\) là trọng tâm tam giác \(ABC\).

Ta có \(A\left( {1;1;1} \right),B\left( { - 1;0;3} \right),C\left( {6;8; - 10} \right)\) nên \(G\left( {2;3; - 2} \right)\)\( \Rightarrow \left\{ \begin{array}{l}M\left( {2;0;0} \right)\\N\left( {0;3;0} \right)\\K\left( {0;0; - 2} \right)\end{array} \right.\)

Vậy phương trình mặt phẳng \(\left( {MNK} \right)\) là: \(\dfrac{x}{2} + \dfrac{y}{3} + \dfrac{z}{{ - 2}} = 1.\)

Chọn B.

Phương pháp giải:

Lời giải chi tiết:

Phương pháp giải:

- Mặt phẳng trung trực của đoạn thẳng \(AB\) đi qua trung điểm của \(AB\) và nhận \(\overrightarrow {AB} \) là 1 VTPT.

- Điểm \(I\) là trung điểm của \(AB\) \( \Rightarrow \left\{ \begin{array}{l}{x_I} = \dfrac{{{x_A} + {x_B}}}{2}\\{y_I} = \dfrac{{{y_A} + {y_B}}}{2}\\{z_I} = \dfrac{{{z_A} + {z_B}}}{2}\end{array} \right.\).

- Mặt phẳng đi qua \(I\left( {a;b;c} \right)\) có 1 VTPT \(\overrightarrow n \left( {A;B;C} \right)\) có phương trình: \(A\left( {x - a} \right) + B\left( {y - b} \right) + C\left( {z - c} \right) = 0\).

Lời giải chi tiết:

Gọi \(I\)  là trung điểm của \(AB\) ta có \(I\left( {\dfrac{1}{2}; - 1; - \dfrac{1}{2}} \right).\)

Gọi \(\left( P \right)\) là mặt phẳng trung trực của \(AB\). Khi đó \(\left( P \right)\) đi qua trung điểm \(I\left( {\dfrac{1}{2}; - 1; - \dfrac{1}{2}} \right)\) của \(AB\) và có 1 vecto pháp tuyến \(\overrightarrow n  = \overrightarrow {BA}  = \left( {3;4;9} \right).\)

Phương trình mặt phẳng \(\left( P \right)\) là:

\(3\left( {x - \dfrac{1}{2}} \right) + 4\left( {y + 1} \right) + 9\left( {z + \dfrac{1}{2}} \right) = 0\)\( \Leftrightarrow 3x + 4y + 9z + 7 = 0\)

Chọn A.

Phương pháp giải:

- Mặt cầu \(\left( S \right):\,\,{x^2} + {y^2} + {z^2} + 2ax + 2by + 2cz + d = 0\) có tâm \(I\left( { - a; - b; - c} \right)\).

- Mặt phẳng tiếp xúc với mặt cầu \(\left( S \right)\) tại \(M\) là mặt phẳng có 1 vecto pháp tuyến là \(\overrightarrow {IM} \) và đi qua điểm \(M\).

- Mặt phẳng đi qua \(M\left( {a;b;c} \right)\) có 1 VTPT \(\overrightarrow n \left( {A;B;C} \right)\) có phương trình: \(A\left( {x - a} \right) + B\left( {y - b} \right) + C\left( {z - c} \right) = 0\).

Lời giải chi tiết:

Mặt cầu \(\left( S \right)\) có tâm là \(I\left( {3;2; - 1} \right).\)

Mà \(M\left( {3;6; - 2} \right) \Rightarrow \overrightarrow {IM}  = \left( {0;4; - 1} \right).\)

Mặt phẳng tiếp xúc với mặt cầu \(\left( S \right)\) tại \(M\) là mặt phẳng có 1 vecto pháp tuyến là \(\overrightarrow {IM} \) và đi qua điểm \(M\) có phương trình:  \(4\left( {y - 6} \right) - \left( {z + 2} \right) = 0\)\( \Leftrightarrow 4y - z - 26 = 0.\)

Chọn A.

Phương pháp giải:

- Tìm 1 VTPT của \(\left( P \right)\) là \(\overrightarrow {{n_P}}  = \left[ {\overrightarrow {AB} ;\overrightarrow {{n_Q}} } \right]\).

- Viết phương trình mặt phẳng \(\left( P \right)\) đi qua \(A\left( {{x_0};{y_0};{z_0}} \right)\) và có 1 VTPT là \(\overrightarrow n \left( {A;B;C} \right)\) là: \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\).

- Xác định \(a,\,\,b,\,\,c\), sau đó tính \(S\).

Lời giải chi tiết:

Ta có: \(\overrightarrow {AB}  = \left( { - 6;3;1} \right)\),\(\overrightarrow {{n_Q}}  = \left( {3;1;1} \right)\).

Do mặt phẳng\(\left( P \right)\) qua \(A\), \(B\) và vuông góc với mặt phẳng \(\left( Q \right)\)nên \(\overrightarrow {{n_P}}  = \left[ {\overrightarrow {AB} ,\overrightarrow {{n_Q}} } \right]\)\( = \left( {2;9; - 15} \right)\).

Suy ra phương trình mặt phẳng\(\left( P \right)\) là: \(2\left( {x - 3} \right) + 9\left( {y - 2} \right) - 15\left( {z - 1} \right) = 0\) \( \Leftrightarrow 2x + 9y - 15z - 9 = 0\).

\( \Rightarrow a = 2,\,\,b = 9,\,\,c =  - 15\).

Vậy \(S = a + b + c\)\( = 2 + 9 - 15\)\( =  - 4\).

Chọn C.

Phương pháp giải:

Tính khoảng cách từ I xuống.

Áp dụng công thức tính diện tích hình tròn.

Áp dụng định lý Pytago để tính bán kính mặt cầu.

Lời giải chi tiết:

Ta có \(I\left( {1;2;0} \right);\left( P \right):2x - 2y + z - 7 = 0\) \( \Rightarrow d\left( {I;\left( P \right)} \right) = \dfrac{{\left| {2.1 - 2.2 + 0 - 7} \right|}}{{\sqrt {4 + 4 + 1} }} = 3.\)

Đường tròn tâm A có \(S = 16\pi  \Rightarrow \pi .A{B^2} = 16\pi  \Rightarrow AB = 4.\)

Áp dụng định lý Pyatgo trong tam giác ABI có \(I{B^2} = I{A^2} + A{B^2} = {3^2} + {4^2} \Rightarrow R = IB = 5\)

Mặt cầu tâm \(I\left( {1;2;0} \right)\) bán kính \(R = 5\) có phương trình là: \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {z^2} = 25.\)

Chọn C.

Phương pháp giải:

- \(\left\{ \begin{array}{l}AB \subset \left( Q \right)\\\left( Q \right) \bot \left( P \right)\end{array} \right. \Rightarrow \overrightarrow {{n_Q}}  = \left[ {\overrightarrow {AB} ;\overrightarrow {{n_P}} } \right]\) với \(\overrightarrow {{n_P}} ,\,\,\overrightarrow {{n_Q}} \) lần lượt là 1 VTPT của \(\left( P \right),\,\,\left( Q \right)\).

- Mặt phẳng đi qua \(M\left( {{x_0};{y_0};{z_0}} \right)\) và có 1 VTPT là \(\overrightarrow n \left( {A;B;C} \right)\) là \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\).

Lời giải chi tiết:

Mặt phẳng \(\left( P \right)\) có 1 VTPT là \(\overrightarrow {{n_P}}  = \left( {2; - 1;2} \right)\).

Ta có: \(A\left( {1;0; - 2} \right);B\left( { - 1; - 1;3} \right)\)\( \Rightarrow \overrightarrow {AB}  = \left( { - 2; - 1;5} \right).\)

\( \Rightarrow \left[ {\overrightarrow {{n_P}} ;\overrightarrow {AB} } \right] = \left( { - 3; - 14; - 4} \right).\).

Gọi \(\overrightarrow {{n_Q}} \) là 1 VTPT của mặt phẳng \(\left( Q \right)\) ta có: \(\left\{ \begin{array}{l}AB \subset \left( Q \right)\\\left( Q \right) \bot \left( P \right)\end{array} \right. \Rightarrow \overrightarrow {{n_Q}}  = \left[ {\overrightarrow {AB} ;\overrightarrow {{n_P}} } \right] = \left( { - 3; - 14; - 4} \right)\) là 1 VTPT của mặt phẳng \(\left( Q \right)\).

Vậy phương trình mặt phẳng \(\left( Q \right)\) là:

\( - 3\left( {x - 1} \right) - 14\left( {y - 0} \right) - 4\left( {z + 2} \right) = 0\) \( \Leftrightarrow 3x + 14y + 4z + 5 = 0\)

Chọn D.

Phương pháp giải:

Hình chiếu của điểm \(M\left( {a;b;c} \right)\) trên mặt phẳng \(\left( {Oyz} \right)\) là điểm \(\left( {0;b;c} \right)\).

Lời giải chi tiết:

Hình chiếu vuông góc của điểm \(M\left( {2; - 2;1} \right)\) trên mặt phẳng \(\left( {Oyz} \right)\) có tọa độ là: \(\left( {0; - 2;1} \right)\).

Chọn C.

Phương pháp giải:

Hai mặt phẳng \(\left( \alpha  \right):\,\,Ax + By + Cz + D = 0\) và \(\left( \beta  \right):\,\,A'x + B'y + C'z + D' = 0\) song song khi và chỉ khi \(\dfrac{A}{{A'}} = \dfrac{B}{{B'}} = \dfrac{C}{{C'}} \ne \dfrac{D}{{D'}}\).

Lời giải chi tiết:

Hai mặt phẳng \(\left( \alpha  \right):\,\,x + 2y - z - 1 = 0\) và \(\left( \beta  \right):\,\,2x + 4y - mz - 2 = 0\) song song với nhau khi và chỉ khi

\(\dfrac{2}{1} = \dfrac{4}{2} = \dfrac{{ - m}}{{ - 1}} \ne \dfrac{{ - 2}}{{ - 1}} \Leftrightarrow \left\{ \begin{array}{l}m = 2\\m \ne  - 2\end{array} \right. \Rightarrow \) Hệ phương trình vô nghiệm.

Vậy không tồn tại m thỏa mãn yêu cầu bài toán.

Chọn B.

Phương pháp giải:

- Nhận xét (P) // (Q).

- \(d\left( {\left( P \right);\left( Q \right)} \right) = d\left( {M;\left( Q \right)} \right)\) với \(M \in \left( P \right)\) bất kì.

- Khoảng cách từ \(M\left( {{x_0};{y_0};{z_0}} \right)\) đến mặt phẳng \(\left( Q \right):\,\,Ax + By + Cz + D = 0\) là

\(d\left( {M;\left( Q \right)} \right) = \dfrac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).

Lời giải chi tiết:

Vì \(\dfrac{2}{4} = \dfrac{{ - 1}}{{ - 2}} = \dfrac{{ - 2}}{{ - 4}} \ne \dfrac{{ - 9}}{{ - 6}}\) nên \(\left( P \right)\parallel \left( Q \right)\).

Xét \(\left( P \right)\), cho \(x = z = 0 \Rightarrow y =  - 9 \Rightarrow M\left( {0; - 9;0} \right) \in \left( P \right)\).

Vậy  \(d\left( {\left( P \right);\left( Q \right)} \right) = d\left( {M;\left( Q \right)} \right) = \dfrac{{\left| { - 2.\left( { - 9} \right) - 6} \right|}}{{\sqrt {{4^2} + {{\left( { - 2} \right)}^2} + {{\left( { - 4} \right)}^2}} }} = 2\).

Chọn B.

Phương pháp giải:

Trong không gian \(Oxyz\), điểm đối xứng với điểm \(M\left( {a;b;c} \right)\) qua mặt phẳng \(\left( {Oyz} \right)\) có tọa độ là \(\left( { - a;b;c} \right)\).

Lời giải chi tiết:

Trong không gian \(Oxyz\), điểm đối xứng với điểm \(M\left( {2; - 2;1} \right)\) qua mặt phẳng \(\left( {Oyz} \right)\) có tọa độ là: \(\left( { - 2; - 2;1} \right)\).

Chọn B.

Phương pháp giải:

- Mặt phẳng \(Ax + By + Cz + D = 0\) có 1 VTPT là \(\overrightarrow n \left( {A;B;C} \right)\).

- Mọi vectơ cùng phương với vectơ \(\overrightarrow n \) đều là 1 VTPT của \(\left( P \right)\).

Lời giải chi tiết:

Ta có \(\dfrac{x}{{ - 5}} + \dfrac{y}{1} + \dfrac{z}{{ - 2}} = 1 \Leftrightarrow 2x - 10y + 5z + 10 = 0\)

Suy ra mặt phẳng có 1 vecto pháp tuyến là \(\overrightarrow n  = \left( {2; - 10;5} \right).\)

Chọn C.

Phương pháp giải:

- Gọi \(H,\,\,K\) lần lượt là hình chiếu của A, B lên (P).

- Sử dụng định lí Ta-lét chứng minh \(\dfrac{{AM}}{{BM}} = \dfrac{{AH}}{{BK}} = \dfrac{{d\left( {A;\left( P \right)} \right)}}{{d\left( {B;\left( P \right)} \right)}}\).

- Tính khoảng cách từ A đến (P): Khoảng cách từ \(A\left( {{x_0};{y_0};{z_0}} \right)\) đến mặt phẳng \(\left( P \right):\,\,Ax + By + Cz + D = 0\) là \({x^3} - x = x - {x^2} \Leftrightarrow {x^3} + {x^2} - 2x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\\x =  - 2\end{array} \right.\).

Lời giải chi tiết:

Vì \(\overrightarrow {AB}  = 3\overrightarrow {AM}  \Rightarrow A;\,\,B\) nằm hai phía của mặt phẳng \(\left( P \right)\) và \(\dfrac{{AM}}{{BM}} = \dfrac{1}{2}\).

Gọi H, K lần lượt là hình chiếu của A, B lên (P). Khi đó ta có AH // BK. Áp dụng định lí Ta-lét ta có: \(\dfrac{{AM}}{{BM}} = \dfrac{{AH}}{{BK}} = \dfrac{{d\left( {A;\left( P \right)} \right)}}{{d\left( {B;\left( P \right)} \right)}} = \dfrac{1}{2}\).

Mà \(d\left( {A;\left( P \right)} \right) = \dfrac{{\left| {3.2 + 4.4 - 12\left( { - 1} \right) + 5} \right|}}{{\sqrt {{3^2} + {4^2} + {{\left( { - 12} \right)}^2}} }} = 3\).

Vậy \(d\left( {B;\left( P \right)} \right) = 2d\left( {A;\left( P \right)} \right) = 6.\)

Chọn C.

Phương pháp giải:

- Tính \(d = d\left( {I;\left( P \right)} \right)\). Khoảng cách từ \(I\left( {{x_0};{y_0};{z_0}} \right)\) đến mặt phẳng\(\left( P \right):Ax + By + Cz + D = 0\) là \(d\left( {I;\left( P \right)} \right) = \dfrac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).

- Sử dụng định lí Pytago: \({R^2} = {r^2} + {d^2}\) với R là bán kính mặt cầu, r là bán kính đường tròn giao tuyến.

- Mặt cầu tâm \(I\left( {a;b;c} \right)\), bán kính \(R\) có phương trình \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\).

Lời giải chi tiết:

Mặt phẳng (P) cắt mặt cầu theo 1 đường tròn có đường kính bằng 8 nên có bán kính r = 4.

Ta có: \(S = \int\limits_{ - 1}^5 {\left| {{x^2} - 4} \right|dx}  = \left| {\int\limits_{ - 1}^2 {\left( {{x^2} - 4} \right)dx} } \right| + \left| {\int\limits_2^5 {\left( {{x^2} - 4} \right)dx} } \right| = 9 + 27 = 36.\)

Gọi R là bán kính mặt cầu (S), áp dụng định lí Pytago ta có: \({R^2} = {r^2} + {d^2} = {4^2} + {3^2} = 25\)

Vậy phương trình mặt cầu là: \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 1} \right)^2} = 25\).

Chọn B.

Phương pháp giải:

- \(\left\{ \begin{array}{l}OA \subset \left( P \right)\\Ox \subset \left( P \right)\end{array} \right. \Rightarrow \left[ {\overrightarrow {OA} ;\overrightarrow i } \right]\) là 1 VTPT của (P).

- \(\overrightarrow n \left( {a;b;c} \right)\) cũng là 1 VTPT của (P) nên \(\overrightarrow n \) cùng phương với vectơ \(\left[ {\overrightarrow {OA} ;\overrightarrow i } \right]\).

Lời giải chi tiết:

Ta có: \(\left\{ \begin{array}{l}OA \subset \left( P \right)\\Ox \subset \left( P \right)\end{array} \right. \Rightarrow \left[ {\overrightarrow {OA} ;\overrightarrow i } \right]\) là 1 VTPT của (P).

\(\overrightarrow {OA}  = \left( {2;1;5} \right),\,\,\overrightarrow i  = \left( {1;0;0} \right)\) \( \Rightarrow \left[ {\overrightarrow {OA} ;\overrightarrow i } \right] = \left( {0;5; - 1} \right)\).

Vì \(\overrightarrow n \left( {a;b;c} \right)\) cũng là 1 VTPT của (P), ta chọn \(\overrightarrow n  = \left[ {\overrightarrow {OA} ;\overrightarrow i } \right] = \left( {0;5; - 1} \right)\) \( \Rightarrow a = 0,\,\,b = 5,\,\,c =  - 1\).

Vậy \(k = \dfrac{b}{c} = \dfrac{5}{{ - 1}} =  - 5\).

Chọn A.

Phương pháp giải:

- Tìm bán kính mặt cầu là khoảng cách từ I đến mặt phẳng \(\left( P \right)\), khoảng cách từ \(I\left( {{x_0};{y_0};{z_0}} \right)\) đến mặt phẳng \(\left( P \right):\,\,Ax + By + Cz + D = 0\) là \(d\left( {I;\left( P \right)} \right) = \dfrac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).

- Mặt cầu tâm \(I\left( {a;b;c} \right)\), bán kính \(R\) có phương trình \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\).

Lời giải chi tiết:

Ta có mặt cầu tâm \(I\left( { - 1;0;0} \right)\) tiếp xúc với \(\left( P \right):x + 2y + 2{\rm{z}} - 5 = 0\) nên \(R = {d_{\left( {I;\left( P \right)} \right)}} = \dfrac{{\left| { - 1 + 2.0 + 2.0 - 5} \right|}}{{\sqrt {1 + 4 + 4} }} = 2.\)

Mặt cầu tâm \(I\left( { - 1;0;0} \right)\) và bán kính \(R = 2\) có phương trình là: \({\left( {x + 1} \right)^2} + {y^2} + {z^2} = 4.\)

Chọn C.

Phương pháp giải:

Áp dụng công thức viết phương trình mặt chắn đi qua 3 điểm đặc biệt có tọa độ \(\left( {a;0;0} \right),\) \(\left( {0;b;0} \right),\) \(\left( {0;0;c} \right)\) là \(\dfrac{x}{a} + \dfrac{y}{b} + \dfrac{z}{c} = 1.\)

Lời giải chi tiết:

Phương trình mặt phẳng đi qua 3 điểm \(E\left( {1;0;0} \right),\) \(N\left( {0;1;0} \right),\)\(M\left( {0;0; - 1} \right)\) là \(\dfrac{x}{1} + \dfrac{y}{1} + \dfrac{z}{{ - 1}} = 1\)\( \Leftrightarrow x + y - z - 1 = 0.\)

Chọn C.

Phương pháp giải:

Sử dụng công thức tính tích có hướng của hai vecto.

Lời giải chi tiết:

Ta có \(M\left( {1;1; - 2} \right),N\left( {3;0;3} \right),P\left( {2;0;0} \right)\)

\( \Rightarrow \left\{ \begin{array}{l}\overrightarrow {MN}  = \left( {2; - 1;5} \right)\\\overrightarrow {MP}  = \left( {1; - 1;2} \right)\end{array} \right. \Rightarrow {\overrightarrow n _{\left( {MNP} \right)}} = \left[ {\overrightarrow {MN} ;\overrightarrow {MP} } \right] = \left( {3;1; - 1} \right)\)

Chọn D.

Phương pháp giải:

- Tìm các vecto pháp tuyến của 3 mặt phẳng.

- Tìm mối quan hệ giữa các vecto rồi kết luận.

Lời giải chi tiết:

Mặt phẳng \(\left( P \right):2x + 4y - 2z + 2 = 0\) có vecto pháp tuyến \(\overrightarrow {{n_1}}  = \left( {2;4; - 2} \right)\)

Mặt phẳng \(\left( Q \right):x + 2y - z = 0\) có vecto pháp tuyến\(\overrightarrow {{n_2}}  = \left( {1;2; - 1} \right)\)

Mặt phẳng \(\left( R \right):x + 2y + z + 3 = 0\) có vecto pháp tuyến \(\overrightarrow {{n_3}}  = \left( {1;2;1} \right)\)

Ta có \(\overrightarrow {{n_1}} \parallel \overrightarrow {{n_2}}  \Rightarrow \left( P \right)\parallel \left( Q \right)\)

Và \(\overrightarrow {{n_2}} .\overrightarrow {{n_3}}  \ne \overrightarrow 0  \Rightarrow \left( Q \right);\left( R \right)\) cắt nhau.

Chọn D.

Phương pháp giải:

- Tìm vecto pháp tuyến của mặt phẳng.

- Viết phương trình mặt phẳng đi qua \(A\left( {{x_0};{y_0};{z_0}} \right)\) và có 1 VTPT là \(\overrightarrow n \left( {A;B;C} \right)\) là:

\(A\left( {x - {x_0}} \right) + \left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\).

Lời giải chi tiết:

Mặt phẳng vuông góc với trục Oy có vecto pháp tuyến là \(\overrightarrow n  = \left( {0;1;0} \right)\)

Mặt phẳng đó đi qua điểm \(M\left( {2;2;3} \right)\) và có dạng \(y - 2 = 0\)

Chọn C.

Phương pháp giải:

- Tìm trung điểm của MN: Trung điểm I đoạn MN có tọa độ là \(\left( {\dfrac{{{x_M} + {x_N}}}{2};\dfrac{{{y_M} + {y_N}}}{2};\dfrac{{{z_M} + {z_N}}}{2}} \right)\).

- Tìm \(\overrightarrow {MN} \) rồi viết phương trình mặt phẳng trung trực là mặt phẳng đi qua I và nhận \(\overrightarrow {MN} \) là 1 VTPT.

- Viết phương trình mặt phẳng đi qua \(A\left( {{x_0};{y_0};{z_0}} \right)\) và có 1 VTPT là \(\overrightarrow n \left( {A;B;C} \right)\) là:

\(A\left( {x - {x_0}} \right) + \left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\).

Lời giải chi tiết:

Mặt phẳng trung trực của đoạn thẳng MN có vecto pháp tuyến là \(\overrightarrow {MN} \) và đi qua trung điểm của MN.

Ta có \(M\left( { - 3;0;3} \right),N\left( {3;0; - 3} \right)\) có trung điểm \(I\left( {0;0;0} \right)\)

Và \(\overrightarrow {MN}  = \left( {6;0; - 6} \right)\) hay \(\left( {1;0; - 1} \right)\)

Mặt phẳng có vecto pháp tuyến là \(\left( {1;0; - 1} \right)\) và đi qua \(I\left( {0;0;0} \right)\) có phương trình là \(x - z = 0\)

Chọn C.

Phương pháp giải:

- Mặt phẳng (P) được gọi là mặt phẳng trung trực của AB nếu (P) đi qua trung điểm của AB và vuông góc với AB.

- Xác định vectơ pháp tuyến của (P): \(\overrightarrow {{n_P}}  = \overrightarrow {AB} \).

- Viết phương trình mặt phẳng đi qua \(A\left( {{x_0};{y_0};{z_0}} \right)\) và có 1 VTPT là \(\overrightarrow n \left( {A;B;C} \right)\) là:

\(A\left( {x - {x_0}} \right) + \left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\).

Lời giải chi tiết:

Ta có: \(\overrightarrow {AB}  = \left( {2; - 4; - 2} \right)\) nên mặt phẳng trung trực của AB có 1 VTPT là \(\overrightarrow n \left( {1; - 2; - 1} \right)\).

Ta có trung điểm I của đoạn AB có tọa độ là \(\left( {2;0;1} \right).\)

Mặt phẳng đi qua I\(\left( {2;0;1} \right)\) và co vecto pháp tuyến là \(\left( {1; - 2; - 1} \right)\) có phương trình là

\(1\left( {x - 2} \right) - 2\left( {y - 0} \right) - \left( {z - 1} \right) = 0\)  \( \Leftrightarrow x - 2y - z - 1 = 0\)

Chọn B.

Phương pháp giải:

- Mặt cầu \(\left( S \right):\,\,{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\) có tâm \(I\left( {a;b;c} \right)\) và bán kính R.

- Hai mặt phẳng song song có cùng VTPT.

- Phương trình mặt phẳng đi qua \(M\left( {{x_0};{y_0};{z_0}} \right)\) và có 1 VTPT \(\overrightarrow n \left( {A;B;C} \right)\) là:

\(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\).

Lời giải chi tiết:

Mặt cầu \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} + {z^2} = 12\) có tâm \(I\left( {1; - 2;0} \right)\).

Mặt phẳng cần tìm song song với mặt phẳng (Oxz) nên có 1 VTPT là \(\overrightarrow j  = \left( {0;1;0} \right)\).

Vậy phương trình mặt phẳng cần tìm là: \(1\left( {y + 2} \right) = 0 \Leftrightarrow y + 2 = 0.\)

Chọn A.

Phương pháp giải:

Tính khoảng cách giữa 2 mặt phẳng song song Ax + By + Cz + D = 0 và Ax + By + Cz + D’ = 0 là \(d = \dfrac{{\left| {D - D'} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).

Lời giải chi tiết:

\(d\left( {\left( P \right),\left( Q \right)} \right) = \dfrac{{\left| { - 11 - 4} \right|}}{{\sqrt {{2^2} + {2^2} + {{\left( { - 1} \right)}^2}} }} = 5.\)

Chọn A.

Phương pháp giải:

Công thức tính khoảng cách từ điểm \(M\left( {{x_0};\,\,{y_0};\,\,{z_0}} \right)\) đến mặt phẳng \(\left( P \right):\,\,ax + by + cz + d = 0\) là: \(d\left( {M;\,\left( P \right)} \right) = \frac{{\left| {a{x_0} + b{y_0} + c{z_0} + d} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}.\)

Lời giải chi tiết:

Ta có: \(d\left( {M;\,\,\left( P \right)} \right) = \frac{{\left| {1 + 2.2 - 2.4 + 5} \right|}}{{\sqrt {1 + {2^2} + {{\left( { - 2} \right)}^2}} }} = \frac{2}{3}.\)

Chọn D.

Phương pháp giải:

Mặt phẳng trung trực \(\left( \alpha  \right)\)  của đoạn thẳng \(AB\)   đi qua trung điểm \(I\) của \(AB\)  và nhận \(\overrightarrow {AB} \) làm VTPT.

Phương trình mặt phẳng đi qua điểm \(M\left( {{x_0};\;{y_0};\;{z_0}} \right)\) và có VTPT \(\overrightarrow n  = \left( {A;\;B;\;C} \right)\) có phương trình: \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0.\)

Lời giải chi tiết:

Ta có: \(\overrightarrow {AB}  = \left( {2;\,\, - 4;\,\,6} \right) = 2\left( {1; - 2;\,\,3} \right).\)  

Gọi \(I\) là trung điểm của \(AB\) \( \Rightarrow I\left( {2;\,\,1;\,\,1} \right).\)

Mặt phẳng trung trực \(\left( \alpha  \right)\)  của đoạn thẳng \(AB\)   đi qua trung điểm \(I\) của \(AB\)  và nhận \(\overrightarrow {AB} \) làm VTPT.

\( \Rightarrow \left( \alpha  \right):\,\,\,x - 2 - 2\left( {y - 1} \right) + 3\left( {z - 1} \right) = 0\)

\( \Leftrightarrow x - 2y + 3z - 3 = 0\)

Chọn A.

Phương pháp giải:

Mặt phẳng \(\left( P \right)//\left( Q \right) \Rightarrow \overrightarrow {{n_P}}  = k\overrightarrow {{n_Q}} .\)

Phương trình mặt phẳng \(\left( P \right)\) đi qua \(M\left( {{x_0};\,{y_0};\,{z_0}} \right)\) và có VTPT \(\overrightarrow n  = \left( {a;\,b;\,c} \right)\) là: \(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) + c\left( {z - {z_0}} \right) = 0.\)

Lời giải chi tiết:

Ta có: \(\overrightarrow {{n_\alpha }}  = \left( {2; - 5;\,\,1} \right).\)

Mặt phẳng cần tìm đi qua \(M\left( {2; - 1;\,\,3} \right)\) và song song với \(\left( \alpha  \right):\,\,\,2x - 5y + z - 1 = 0\) có phương trình:

\(2\left( {x - 2} \right) - 5\left( {y + 1} \right) + z - 3 = 0\) \( \Leftrightarrow 2x - 5y + z - 12 = 0.\)

Chọn A.

Phương pháp giải:

- Mặt phẳng trung trực của AB đi qua trung điểm của AB và nhận \(\overrightarrow {AB} \) là 1 VTPT.

- Phương trình mặt phẳng đi qua \(M\left( {{x_0};{y_0};{z_0}} \right)\) và có 1 VTPT \(\overrightarrow n \left( {A;B;C} \right)\) là:

\(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\).

Lời giải chi tiết:

Gọi I là trung điểm của AB ta có \(I\left( {\dfrac{1}{2};\dfrac{3}{2};\dfrac{1}{2}} \right)\).

Mặt phẳng trung trực của AB đi qua I và nhận \(\overrightarrow {AB}  = \left( {3; - 1; - 1} \right)\) là 1 VTPT.

Vậy phương trình mặt phẳng trung trực của AB là:

\(3\left( {x - \dfrac{1}{2}} \right) - 1.\left( {y - \dfrac{3}{2}} \right) - 1.\left( {z - \dfrac{1}{2}} \right) = 0\) \( \Leftrightarrow 3x - y - z + \dfrac{1}{2} = 0\) \( \Leftrightarrow 6x - 2y - 2z + 1 = 0\).

Chọn D.

Phương pháp giải:

- Vectơ pháp tuyến của mặt phẳng trung trực của AB là \(\overrightarrow {AB} \).

- Tìm trung điểm I của AB là điểm thuộc mặt phẳng cần tìm.

Lời giải chi tiết:

Gọi mặt phẳng trung trực của AB là mặt phẳng \(\left( P \right)\).

Gọi I là trung điểm của AB \( \Rightarrow I\left( {2;0;1} \right)\).

Ta có: \(\overrightarrow {AB}  = \left( { - 2; - 2;2} \right) \Rightarrow \overrightarrow n  = \left( {1;1; - 1} \right)\) là 1 VTPT của \(\left( P \right)\).

Vậy phương trình mặt phẳng \(\left( P \right)\) là: \(1\left( {x - 2} \right) + 1\left( {y - 0} \right) - 1\left( {z - 1} \right) = 0\)\( \Leftrightarrow x + y - z - 1 = 0\).

Chọn B.

Phương pháp giải:

Góc giữa hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) là \(\cos \angle \left( {\left( P \right);\left( Q \right)} \right) = \dfrac{{\left| {\overrightarrow {{n_P}} .\overrightarrow {{n_Q}} } \right|}}{{\left| {\overrightarrow {{n_P}} } \right|.\left| {\overrightarrow {{n_Q}} } \right|}}\) với \(\overrightarrow {{n_P}} ,\,\,\overrightarrow {{n_Q}} \) lần lượt là 1 VTPT của mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\).

Lời giải chi tiết:

Mặt phẳng \(\left( P \right):x - 2y - z + 2 = 0\) có 1 VTPT là \(\overrightarrow {{n_P}} \left( {1; - 2; - 1} \right)\).

Mặt phẳng \(\left( Q \right):x - 2y - z + 2 = 0\) có 1 VTPT là \(\overrightarrow {{n_Q}} \left( {2; - 1;1} \right)\).

Khi đó ta có: \(\cos \angle \left( {\left( P \right);\left( Q \right)} \right) = \dfrac{{\left| {\overrightarrow {{n_P}} .\overrightarrow {{n_Q}} } \right|}}{{\left| {\overrightarrow {{n_P}} } \right|.\left| {\overrightarrow {{n_Q}} } \right|}}\)\( = \dfrac{{\left| {1.2 - 2.\left( { - 1} \right) - 1.1} \right|}}{{\sqrt {{1^2} + {{\left( { - 2} \right)}^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{2^2} + {{\left( { - 1} \right)}^2} + {1^2}} }} = \dfrac{3}{6} = \dfrac{1}{2}\).

Vậy \(\angle \left( {\left( P \right);\left( Q \right)} \right) = {60^0}\).

Chọn A.

Phương pháp giải:

- Tìm tọa độ trung điểm \(I\) của đoạn thẳng \(AB\): \(\left\{ \begin{array}{l}{x_I} = \dfrac{{{x_A} + {x_B}}}{2}\\{y_I} = \dfrac{{{y_A} + {y_B}}}{2}\\{z_I} = \dfrac{{{z_A} + {z_B}}}{2}\end{array} \right.\).

- Mặt phẳng trung trực của đoạn thẳng \(AB\) đi qua \(I\) và nhận \(\overrightarrow {AB} \) là 1 VTPT.

- Phương trình mặt phẳng đi qua \(M\left( {{x_0};{y_0};{z_0}} \right)\) và có 1 VTPT \(\overrightarrow n \left( {A;B;C} \right)\) có phương trình là:

\(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\).

Lời giải chi tiết:

Gọi \(I\) là trung điểm của \(AB\) ta có \(I\left( {2;1;2} \right)\).

Ta có \(\overrightarrow {AB}  = \left( {2; - 2;0} \right)\) \( \Rightarrow \overrightarrow n  = \dfrac{1}{2}\overrightarrow {AB}  = \left( {1; - 1;0} \right)\) là 1 VTPT của mặt phẳng trung trực của \(AB\).

Vậy phương trình mặt phẳng trung trực của \(AB\) là:

\(1\left( {x - 2} \right) - 1\left( {y - 1} \right) + 0\left( {z - 2} \right) = 0 \Leftrightarrow x - y - 1 = 0\).

Chọn B.

Phương pháp giải:

Hai mặt phẳng song song với nhau khi và chỉ khi hai VTPT của hai mặt phẳng cùng phương.

Lời giải chi tiết:

Mặt phẳng \(\left( P \right):\,\,\,3x - my - z + 7 = 0\) có 1 VTPT \(\overrightarrow {{n_P}}  = \left( {3; - m; - 1} \right)\).

Mặt phẳng \(\left( Q \right):\,\,\,6x + 5y - 2z - 4 = 0\) có 1 VTPT \(\overrightarrow {{n_Q}}  = \left( {6;5; - 2} \right)\).

Để \(\left( P \right)\parallel \left( Q \right)\) thì \(\overrightarrow {{n_P}} ,\,\,\overrightarrow {{n_Q}} \) cùng phương \( \Leftrightarrow \dfrac{3}{6} = \dfrac{{ - m}}{5} = \dfrac{{ - 1}}{{ - 2}} \Leftrightarrow m =  - \dfrac{5}{2}\).

Chọn A.

Phương pháp giải:

- Mặt phẳng song song với \(\left( P \right):\,\,x - 2y + z + 3 = 0\) có dạng \(\left( Q \right):\,\,x - 2y + z + d = 0\,\,\left( {d \ne 3} \right)\).

- Thay tọa độ điểm \(M\left( {1;2;3} \right)\) vào phương trình mặt phẳng\(\left( Q \right)\) tìm hằng số \(d\) và kết luận phương trình mặt phẳng cần tìm.

Lời giải chi tiết:

Gọi \(\left( Q \right)\) là mặt phẳng cần tìm.

Vì \(\left( Q \right)\parallel \left( P \right)\) nên phương trình mặt phẳng \(\left( Q \right)\) có dạng: \(\left( Q \right):\,\,x - 2y + z + d = 0\,\,\left( {d \ne 3} \right)\).

Theo bài ra ta có: \(M\left( {1;2;3} \right) \in \left( Q \right)\).

\( \Rightarrow 1 - 2.2 + 3 + d = 0 \Leftrightarrow d = 0\) (thỏa mãn).

Vậy phương trình mặt phẳng \(\left( Q \right)\) cần tìm là: \(x - 2y + z = 0\).

Chọn C.

Phương pháp giải:

Mặt phẳng đi qua \(M\left( {{x_0};{y_0};{z_0}} \right)\) và có VTPT \(\overrightarrow n  = \left( {a;b;c} \right)\) có phương trình \(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right)\)\( + c\left( {z - {z_0}} \right) = 0\)

Lời giải chi tiết:

Ta có VTPT của \(\left( \alpha  \right)\) là \(\overrightarrow {{n_\alpha }}  = \left( {3; - 1;2} \right)\)

Vì mặt phẳng cần tìm song song với \(\left( \alpha  \right)\) nên nhận \(\overrightarrow n  = \overrightarrow {{n_\alpha }}  = \left( {3; - 1;2} \right)\) làm VTPT

Phương trình mặt phẳng đó là: \(3\left( {x - 3} \right) - 1\left( {y + 1} \right) + 2\left( {z + 2} \right) = 0\) \( \Leftrightarrow 3x - y + 2z - 6 = 0\)

Chọn B.

Phương pháp giải:

Mặt phẳng trung trực \(\left( \alpha  \right)\)  của đoạn thẳng \(AB\)   đi qua trung điểm \(I\) của \(AB\)  và nhận \(\overrightarrow {AB} \) làm VTPT.

Lời giải chi tiết:

Ta có: \(A\left( {1;\,\,2;\,\,3} \right)\) và \(B\left( {3;\,\,4;\,\,7} \right)\)\( \Rightarrow \overrightarrow {AB}  = \left( {2;\,\,2;\,\,4} \right) = 2\left( {1;\,\,1;\,\,2} \right)\)

Gọi \(I\) là trung điểm của \(AB\) \( \Rightarrow I\left( {2;\,\,3;\,\,5} \right)\)

Mặt phẳng trung trực \(\left( \alpha  \right)\)  của đoạn thẳng \(AB\)   đi qua trung điểm \(I\) của \(AB\)  và nhận \(\overrightarrow {AB} \) làm VTPT

\( \Rightarrow \left( \alpha  \right):\,\,\,x - 2 + y - 3 + 2\left( {z - 5} \right)\) \( \Leftrightarrow x + y + 2z - 15 = 0\)

Chọn A.

Phương pháp giải:

Cho \(\left( \alpha  \right):\,\,\,Ax + By + Cz + D = 0\) và  \(\left( \beta  \right):\,\,\,ax + by + cz + d = 0\)

\( \Rightarrow \) Mặt phẳng \(\left( \alpha  \right)//\left( \beta  \right)\)  \( \Leftrightarrow \dfrac{A}{a} = \dfrac{B}{b} = \dfrac{C}{c} \ne \dfrac{D}{d}.\)

Lời giải chi tiết:

Ta có: \(\left( \alpha  \right):\,\,x + y - z + 1 = 0\) có VTPT là: \(\overrightarrow {{n_\alpha }}  = \left( {1;\,\,1; - 1} \right).\)

\(\left( \beta  \right):\,\,\, - 2x + my + 2z - 2 = 0\) có VTPT là: \(\overrightarrow {{n_\beta }}  = \left( { - 2;\,\,m;\,\,2} \right).\)

\( \Rightarrow \left( \alpha  \right)//\left( \beta  \right) \Leftrightarrow \dfrac{{ - 2}}{1} = \dfrac{m}{1} = \dfrac{2}{{ - 1}} \ne \dfrac{{ - 2}}{1}\) (vô lý)

\( \Rightarrow \) Không có giá trị của \(m\) thỏa mãn bài toán.

Chọn B.

Phương pháp giải:

Mặt phẳng vuông góc với \(AB\) nhận \(\overrightarrow {AB} \) làm VTPT.

Phương trình mặt phẳng đi qua điểm \(M\left( {{x_0};\;{y_0};\;{z_0}} \right)\) và có VTPT \(\overrightarrow n  = \left( {A;\;B;\;C} \right)\) có phương trình: \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0.\)

Lời giải chi tiết:

Ta có: \(\overrightarrow {AB}  = \left( {2; - 4;\,\,4} \right) = 2\left( {1; - 2;\,\,2} \right)\)

Mặt phẳng \(\left( P \right)\)  cần tìm vuông góc với \(AB\) \( \Rightarrow \) nhận vecto \(\left( {1;\, - 2;\,\,2} \right)\) làm VTPT.

\( \Rightarrow \left( P \right)\) đi qua \(A\left( {1;\,\,3; - 1} \right)\) và vuông góc với \(AB\) có phương trình:

\(x - 1 - 2\left( {y - 3} \right) + 2\left( {z + 1} \right) = 0\) \( \Leftrightarrow x - 2y + 2z + 7 = 0.\) 

Chọn D.

Phương pháp giải:

Cho ba điểm \(A\left( {a;\,\,0;\,\,0} \right),\,\,B\left( {0;\,\,b;\,\,0} \right)\) và \(C\left( {0;\,\,0;\,\,c} \right).\) Khi đó phương trình mặt phẳng \(\left( {ABC} \right)\) có dạng:

\(\dfrac{x}{a} + \dfrac{y}{b} + \dfrac{z}{c} = 1\) được gọi là phương trình mặt chắn.

Lời giải chi tiết:

Phương trình mặt phẳng \(\left( {MNP} \right)\) đi qua ba điểm \(M\left( {1;\,\,0;\,\,0} \right),\,\,N\left( {0; - 2;\,\,0} \right),\,\,P\left( {0;\,\,0;\,\,3} \right)\) có dạng:

\(\dfrac{x}{1} - \dfrac{y}{2} + \dfrac{z}{3} = 1.\)

Chọn A.

Phương pháp giải:

Mặt phẳng vuông góc với \(AB\) nhận \(\overrightarrow {AB} \) làm VTPT.

Phương trình mặt phẳng đi qua điểm \(M\left( {{x_0};\;{y_0};\;{z_0}} \right)\) và có VTPT \(\overrightarrow n  = \left( {A;\;B;\;C} \right)\) có phương trình: \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0.\)

Lời giải chi tiết:

Ta có: \(\overrightarrow {AB}  = \left( {1; - 2;\,\,2} \right)\)

Mặt phẳng \(\left( P \right)\)  cần tìm vuông góc với \(AB\) \( \Rightarrow \) nhận vecto \(\left( {1;\, - 2;\,\,2} \right)\) làm VTPT.

\( \Rightarrow \left( P \right)\) đi qua \(A\left( {1;\,\,2;\,\,3} \right)\) và vuông góc với \(AB\) có phương trình:

\(x - 1 - 2\left( {y - 2} \right) + 2\left( {z - 3} \right) = 0\) \( \Leftrightarrow x - 2y + 2z - 3 = 0.\) 

Chọn D.

Phương pháp giải:

Công thức tính khoảng cách từ điểm \(M\left( {{x_0};\,\,{y_0};\,\,{z_0}} \right)\) đến mặt phẳng \(\left( P \right):\,\,ax + by + cz + d = 0\) là: \(d\left( {M;\,\left( P \right)} \right) = \frac{{\left| {a{x_0} + b{y_0} + c{z_0} + d} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}.\)

Lời giải chi tiết:

Ta có:\(\left( P \right):\,\,\,2x - 2y + z - 2 = 0\)

\( \Rightarrow d\left( {M;\,\,\left( P \right)} \right) = \frac{{\left| {2.1 - 2.6 - 3 - 2} \right|}}{{\sqrt {{2^2} + {{\left( { - 2} \right)}^2} + 1} }}\) \( = \frac{{15}}{3} = 5.\)

Chọn A.

Phương pháp giải:

- Mặt phẳng trung trực của đoạn thẳng \(AB\) đi qua trung điểm của \(AB\) và nhận \(\overrightarrow {AB} \) là 1 VTPT.

- Phương trình mặt phẳng đi qua \(M\left( {{x_0};{y_0};{z_0}} \right)\) và có 1 VTPT \(\overrightarrow n \left( {A;B;C} \right)\) là:

\(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\).

Lời giải chi tiết:

Diện tích \(S\) của hình phẳng giới hạn bởi các đường \(y = 2x\), \(x =  - 3\), \(x =  - 2\) và trục hoành là: \(S = \int\limits_{ - 3}^{ - 2} {\left| {2x} \right|dx} \).

Trên khoảng \(\left( { - 3; - 2} \right)\) ta có \(\left| {2x} \right| =  - 2x\), do đó \(S = \int\limits_{ - 3}^{ - 2} { - 2xdx}  = \int\limits_{ - 2}^{ - 3} {2xdx} \).

Chọn A.

Phương pháp giải:

- Xác định tâm \(I\) và bán kính \(R\) của mặt cầu \(\left( S \right)\): Mặt cầu \(\left( S \right):\,\,\,{x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) có tâm \(I\left( {a;b;c} \right)\), bán kính \(R = \sqrt {{a^2} + {b^2} + {c^2} - d} \).

- Mặt phẳng \(\left( P \right)\) tiếp xúc với mặt cầu \(\left( S \right)\) tại \(A\) nhận \(\overrightarrow {IA} \) là 1 VTPT.

- Phương trình mặt phẳng đi qua \(A\left( {{x_0};{y_0};{z_0}} \right)\) và có 1 VTPT \(\overrightarrow n \left( {A;B;C} \right)\) là: \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\)

Lời giải chi tiết:

Mặt cầu \(\left( S \right):\,\,\,{x^2} + {y^2} + {z^2} - 2x - 4y - 4z = 0\) có tâm \(I\left( {1;2;2} \right)\), bán kính \(R = \sqrt {{1^2} + {2^2} + {3^2} - 0}  = \sqrt {14} \).

Gọi \(\left( P \right)\) là mặt phẳng tiếp xúc với mặt cầu \(\left( S \right)\) tại \(A\left( {3;4;3} \right)\), khi đó ta có \(IA \bot \left( P \right)\) nên \(\left( P \right)\) nhận \(\overrightarrow {IA}  = \left( {2;2;1} \right)\) là 1 VTPT.

Vậy phương trình mặt phẳng \(\left( P \right)\) đi qua \(A\left( {3;4;3} \right)\) và có 1 VTPT \(\overrightarrow {IA}  = \left( {2;2;1} \right)\) là:

\(2\left( {x - 3} \right) + 2\left( {y - 4} \right) + 1\left( {z - 3} \right) = 0\) \( \Leftrightarrow 2x + 2y + z - 17 = 0\).

Chọn A.

Phương pháp giải:

- Mặt phẳn đi qua A và vuông góc với đường thẳng BC nhận \(\overrightarrow {BC} \) là 1 VTPT.

- Phương trình mặt phẳng đi qua \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có 1 VTPT \(\overrightarrow n \left( {a;b;c} \right) \ne \overrightarrow 0 \) là:

\(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) + c\left( {z - {z_0}} \right) = 0\).

Lời giải chi tiết:

Ta có: \(\overrightarrow {BC}  = \left( { - 4;4; - 2} \right)\) là 1 VTPT của mặt phẳng qua A và vuông góc với đường thẳng BC.

Mặt phẳng đi qua A và vuông góc với đường thẳng BC nhận \(\overrightarrow {BC}  = \left( { - 4;4; - 2} \right)\) là VTPT, có phương trình là:

\( - 4\left( {x - 1} \right) + 4\left( {y - 1} \right) - 2\left( {z + 2} \right) = 0\)\( \Leftrightarrow  - 4x + 4y - 2z - 4 = 0\) \( \Leftrightarrow 2x - 2y + z + 2 = 0\)

Chọn B.